路漫漫其修远兮，吾将上下而求索。
　　　　　　　　　　　　　　　　——屈原

　　　　　　　　　　

　　在最短路径的求解算法中，迪杰斯特拉（Dijkstra）算法应该是非常出名的，但是对于初学者而言却又很难理解为什么这个算法是对的，找到的就是最短路径。下面博主参考了相关资料，和大家谈谈如何理解迪杰斯特拉算法。

一、松弛（relaxation）

　　所谓“松弛”是从国外的文献资料上的单词“relaxation”直译而来的，亦可以翻译成“弛豫”。那么，到底什么是松弛呢？
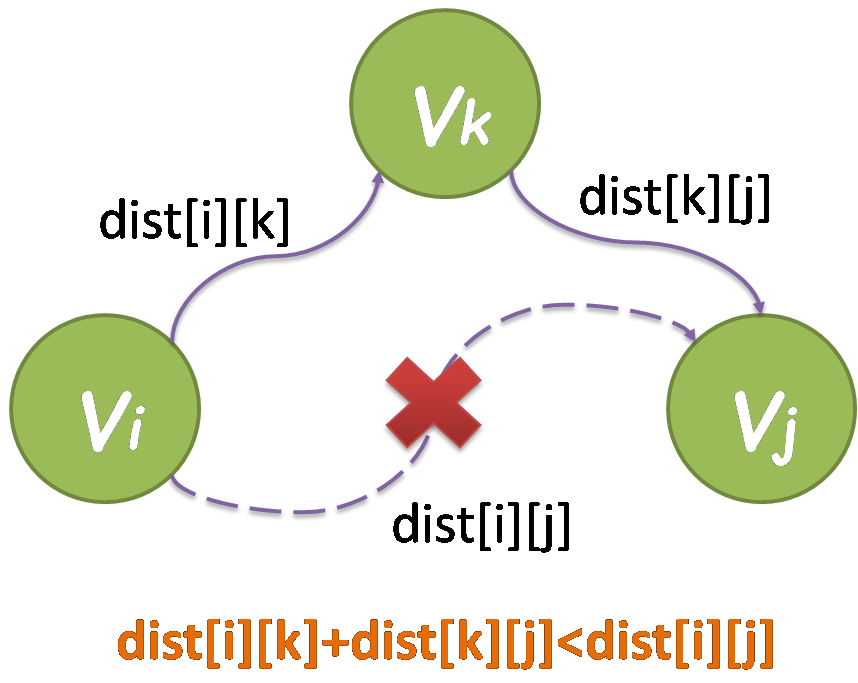
　　我们先来看下面这张图片。

　　上图中，原来认为顶点$v_{i}$到$v_{j}$的最短路径为虚线所标的路径$v_{i}$->$v_{j}$。而当将$v_{k}$这个顶点拉进$v_{i}$和$v_{j}$之间后，发现$dist[i][k]＋dist[k][j]＜dist[i][j]$，即从顶点$v_{i}$出发，先经过$v_{i}$->$v_{k}$这条路，再经过$v_{k}$->$v_{j}$这条路，最后抵达$v_{j}$顶点的路径长度比$v_{i}$->$v_{j}$这条路要短，所以放弃原来虚线的那条路，而选择新发现的这条路。
　　上述过程就是所谓的“松弛”，即好像将原来“紧绷”的“弦”（路$v_{i}$->$v_{j}$）通过顶点$v_{k}$将它“拉开”，也就“松了下来”。

二、（最优子结构）从$v_{i}$到$v_{j}$的最短路上所经过的顶点$v_{k}$一定满足$v_{i}$到$v_{k}$的路径为最短路

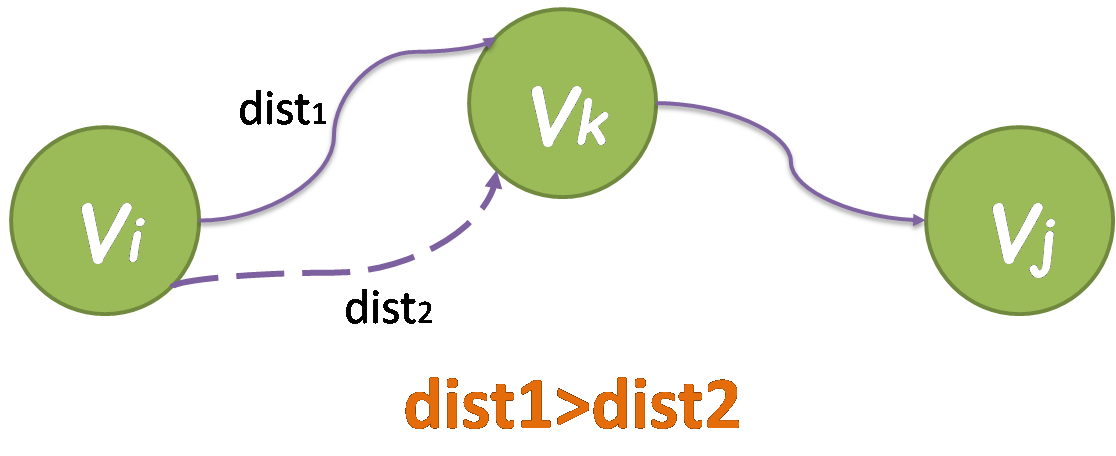
　　标题中所给出的结论是显然的。下面我们通过反证法做一些论证。

　　假设已知上图中实线所示的路径为$v_{i}$至$v_{j}$的最短路径，而现在又发现$v_{i}$到$v_{k}$之间还存在着另一条比$v_{i}$到$v_{k}$的实线路径还要短的路径，即虚线路径。那么$v_{i}$到$v_{k}$的最短路径就应该是从$v_{i}$出发，经过虚线路径到达$v_{k}$，再沿着实线路径抵达$v_{j}$。这与我们先前的假设矛盾！所以，从$v_{i}$到$v_{j}$的最短路上所经过的顶点$v_{k}$一定满足$v_{i}$到$v_{k}$的路径为最短路。

三、（贪心选择性质）对于无负权环的图$G$，若顶点$v$所对应的距离为$V-U$中顶点在距离表中的最小值，则源点到$v$的最短路已经找到

　　上述结论中，$V$指图$G$中的所有顶点集合，$U$指已经找到从源点出发至该点的最短路的顶点集合。
　　首先介绍距离表。所谓距离表，就是记录当前求得的从源点$v_{i}$到该点的最短路径长度。
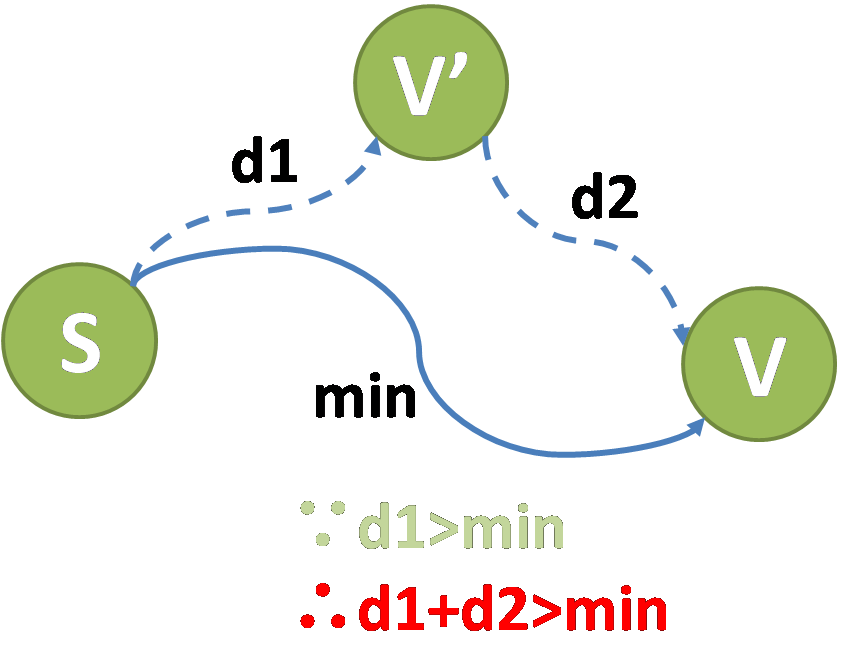
　　依然利用反证法论述上述结论。
　　假如该最小值所对应的顶点$v$的单源最短路径并不是当前求得的路径，那么可以找到另外某个$V-U$的其他顶点$v'$通过松弛操作，使得$s$至$v$的路径更短。而由于$s$至$v'$的距离已经比$s$至$v$的距离长，那么无法通过松弛操作找到更短的路径。
　　但是，上述论述都需要一个前提，就是图中不含负权环！

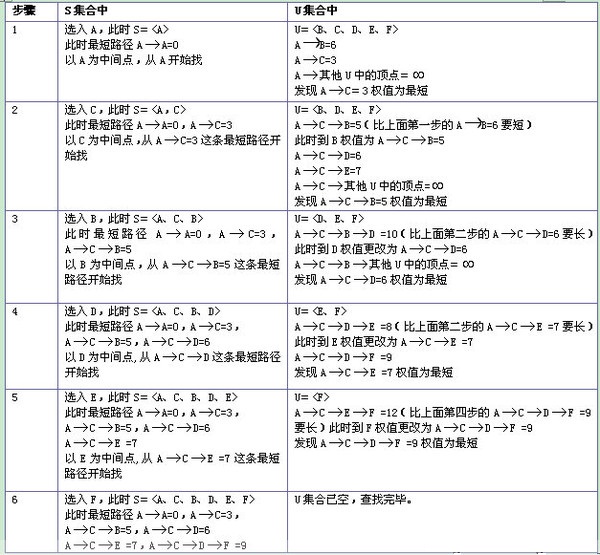
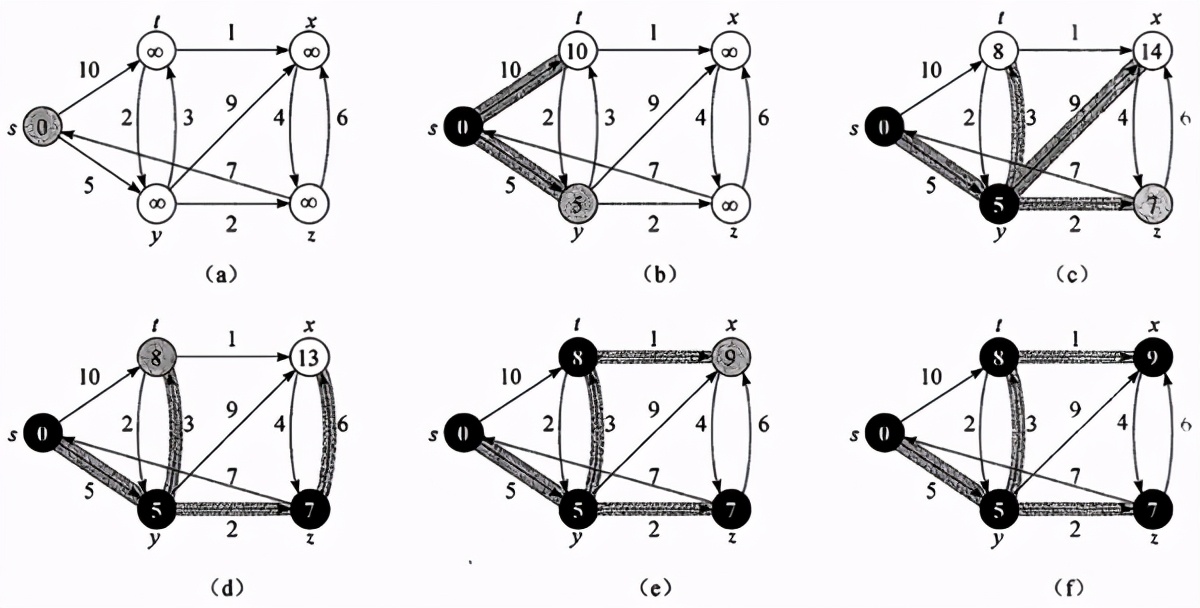
四、迪杰斯特拉算法的运行过程

　　下面，终于正式进入迪杰斯特拉算法的解释。
　　首先，我们需要开两个集合$U$和$V-U$，其中$V$为图$G$的所有顶点集合，$U$为已经求得从源点$v_{i}$到该点的最短路径的那些顶点。
　　同时我们还要开一个表，来记录当前求得的从源点$v_{i}$到该点的最短路径长度，即距离表。
　　初始时，集合$U$中只有源点$v_{i}$，而$V-U$中就是$V-\{v_{i}\}$，表中就是vi到该顶点一步可达路径的距离，若不存在一步可达，就记录为$∞$。
接着每一次循环都将距离表中最短距离所对应的顶点拉入集合$U$中，并利用新加入的顶点对$V-U$中的顶点依次做松弛，若经过新顶点的路径距离比原来的要小，则更新距离表中的值。
　　对于上一步骤的正确性，前文已经给出解释。首先，认为距离表中$V-U$集合中的顶点所对应的距离值最小者所对应的顶点，即为最新发现的从源点发出的至一点的最短路径，那么还未找到最短路径的其他顶点的最短路势必要经过这个顶点或者$U$中的其他顶点。
如此的循环下去直到所有顶点都被拉入集合$U$中为止。
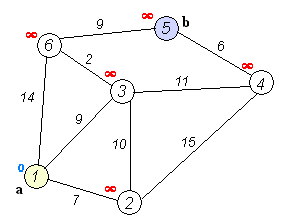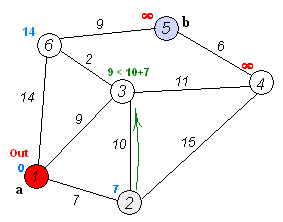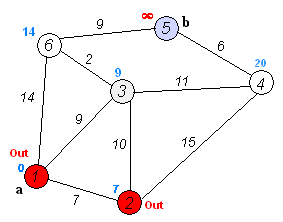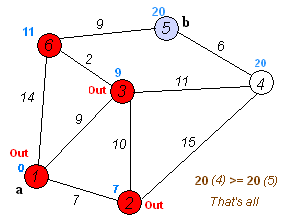
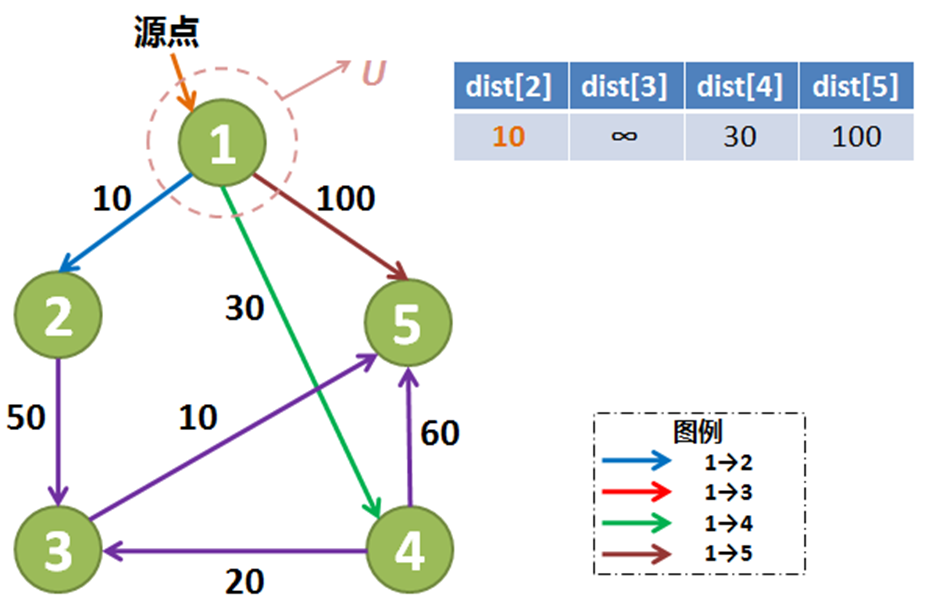
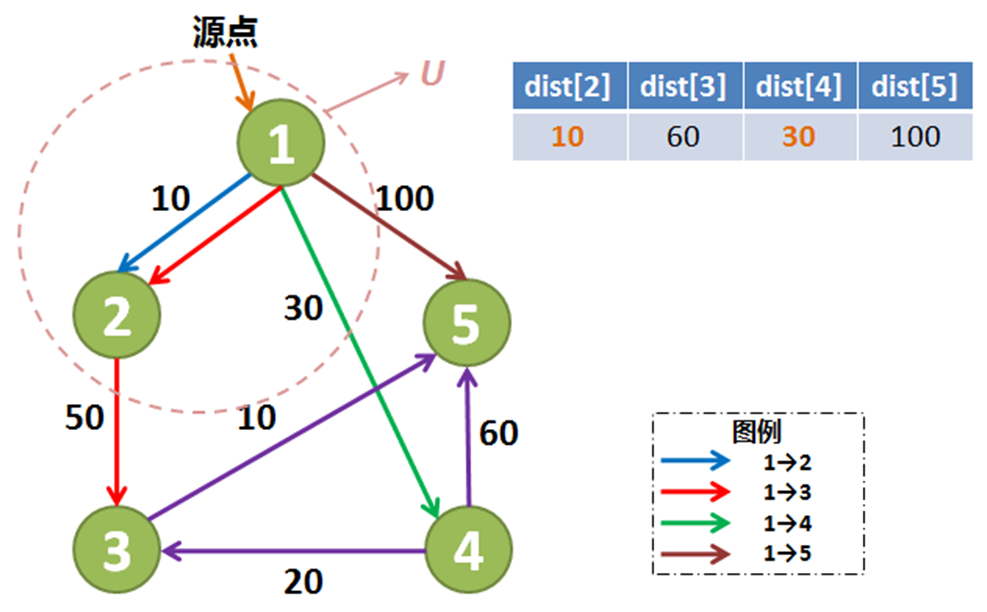
　　可以从下面的例子来理解上述过程。

　　下面，从距离表中找到距离最小的顶点2，然后将2号顶点加入集合$U$中，并且对1号顶点到$V-U$集合中的顶点，通过2号顶点做松弛，将距离表更新。

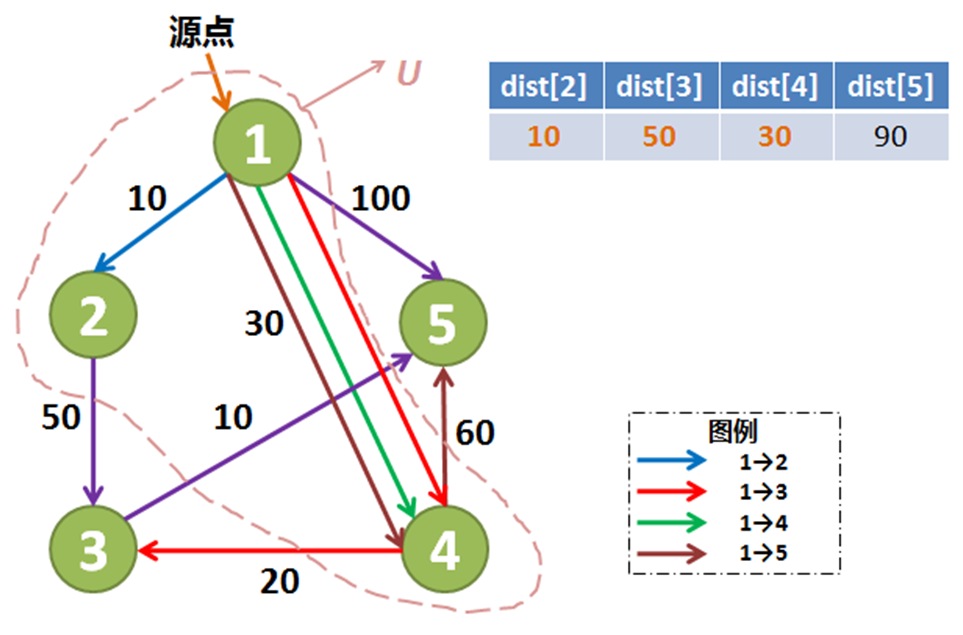
　　在距离表中找到最小值30，将对应的4号顶点拉进集合$U$，对集合$V-U$中的顶点再做一次松弛。

　　在距离表中找到最小值50，将对应的3号顶点拉进集合$U$，对集合$V-U$中的顶点再做一次松弛。

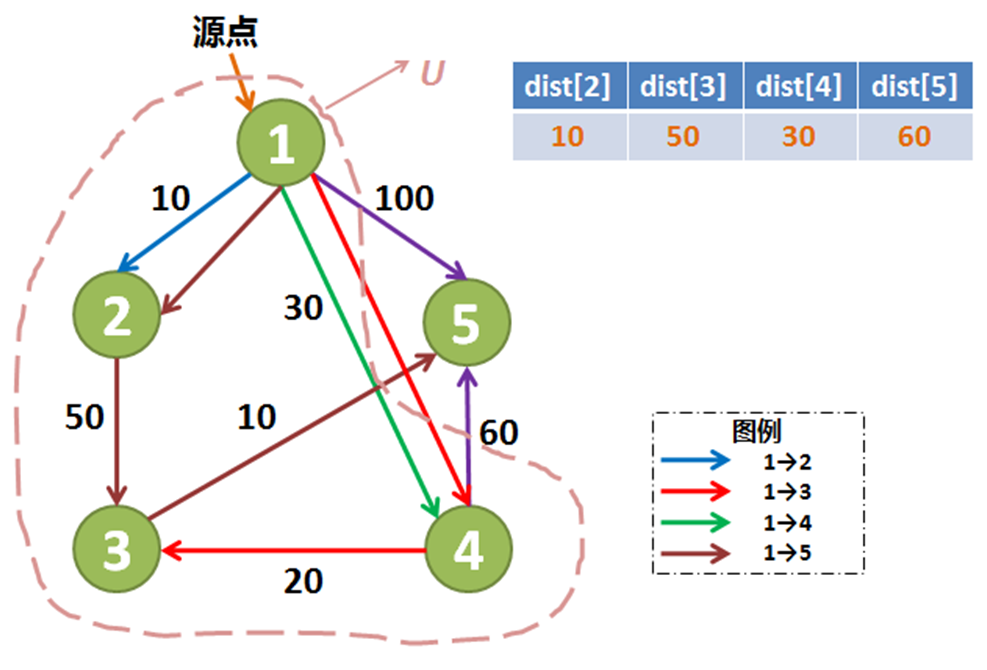
　　再将5号顶点拉入集合$U$中，由于$V-U$已经为空，不需要再做新的更新。至此，算法结束，从源点至其他各个顶点的最短路径都已经找到。

五、存在的问题

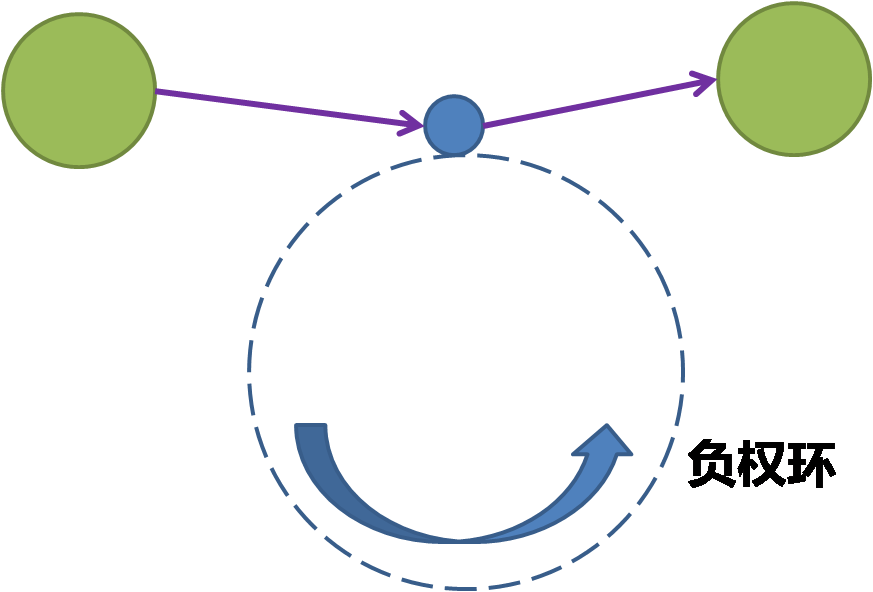
　　由于上述更新的过程中，如果发现顶点$v_{i}$到$v_{j}$经过新加入的顶点$v_{k}$所得到的路径长度比原来的更短，就对距离表做修改。只要该顶点当前的距离是$V-U$中顶点在表中数值的最小值，就认为该顶点的最短路已经找到，而不会对其再做更新。即认为：距离表中$V-U$集合中的顶点所对应的距离值最小者所对应的顶点，即为最新发现的从源点发出的至一点的最短路径。而这个认为并非总是成立。事实上，如果$G$中存在负权环，即存在一个圈，该圈上的权值之和为负值，那么每走一次圈，距离就会减小一些，那么就不存在最小距离之说，因为距离可以达到负无穷大。也就是说，距离表中所谓的“最小值”并非真正的最小值，我们总还是能够找到比起更小的值。那么算法正确性就没了保证。

　　那么，我们该怎么面对带有负权环的图呢？历史上，Richard Bellman和Lester Ford等人给出了他们的解决方案，称为Bellman-Ford算法，它可以帮助我们判断$G$中是否存在负权环，同时在负权环不存在的情况下给出单源最短路径。对于该算法，这里不做过多介绍，大家可以去查阅相关资料学习。

参考资料：

[1] 最短路径算法——Dijkstra（迪杰斯特拉）算法分析与实现（C/C++）
[2] 算法（第4版），塞奇威克（Robert Sedgewick）、韦恩（Kevin Wayne）著