半导体器件-MOS管
- MOS管
- MOS管器件符号
- MOS器件结构
- 集成电路版图中的MOS
- MOS管的工作状态及相关参数
- 过程一(都接地)
- 过程二(形成耗尽层)
- 过程三(形成反型层)
- 过程四(形成电流)
- 过程五(沟道夹断:进入饱和区)
- 过程六(饱和区)
- 重要参数—阈值电压
- I/V特性曲线
- 电流密度与电荷密度的基本概念
- 电流棒中的电流密度
- NMOS管中未夹断时的电荷密度
- NMOS管中夹断时的电荷密度
- 构建等式(MOS管中的电流公式)
- MOS管一级模型
- 三极管区/可变电阻区
- 过驱动电压
- 饱和区/恒流区
- 模拟CMOS设计最基本的方程式
- 合并两个I/V曲线
MOS管
MOS管器件符号
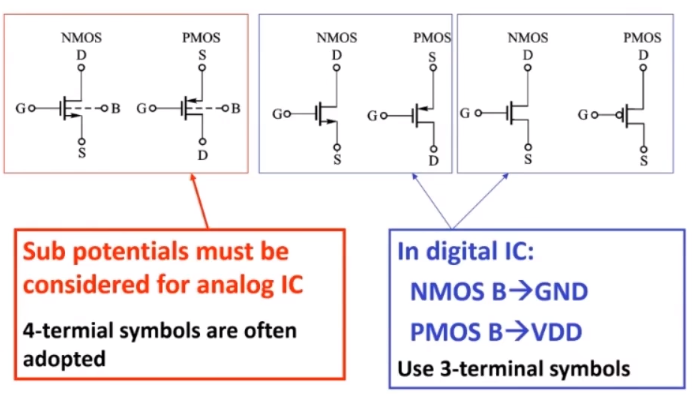
- 在集成电路设计中,对于模拟集成电路来说,衬底是不可忽略的设计对象,衬底的掺杂浓度决定了很多因素,所以往往在模拟集成电路中,把MOS管看成一个四端口器件;而对于数字电路来说,要求没那么苛刻,则可看成三端口器件。
MOS器件结构
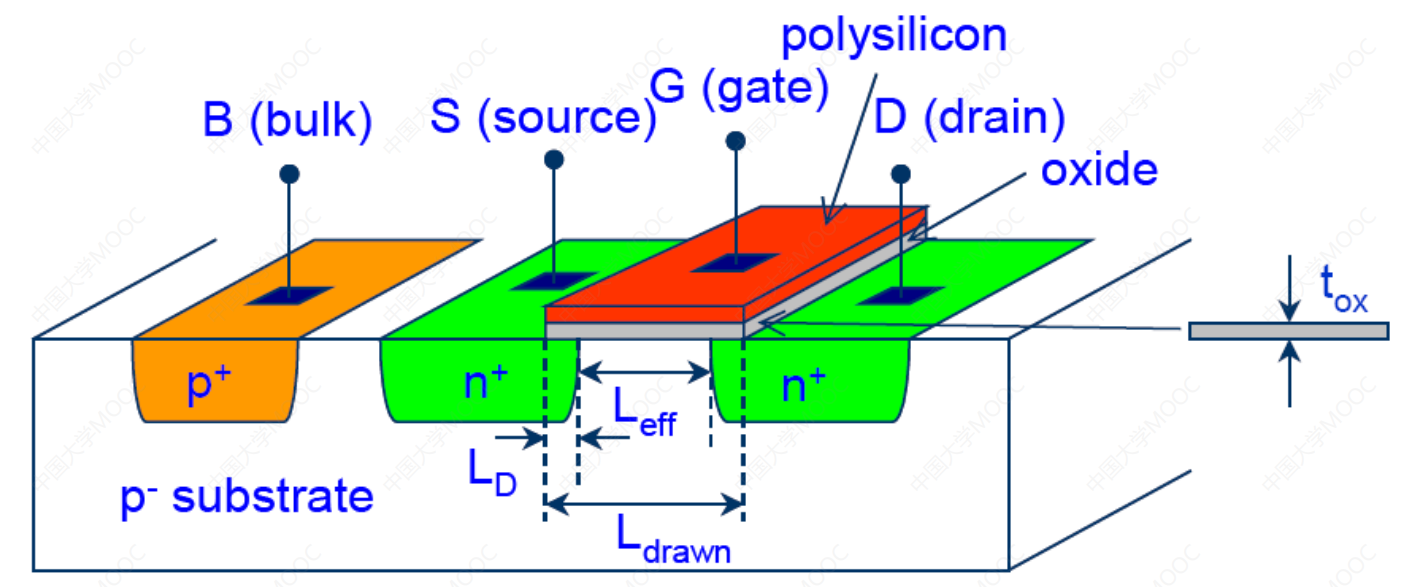
- 结构:
- 红色:多晶硅形成的栅极G(gate);
- 绿色:源极S(source)和漏极D(drain);
- 黄色:衬底B(bulk);
- 物理尺寸:
- 源-漏极之间有一定距离,称为沟道长度;
- Leff:有效沟道长度;
- Ldrawn:沟道绘制长度;
- LD:栅横向扩散长度;
- tox:栅极绝缘层;
- 集成电路设计者可以决定的是:
- W/L:宽长比,其中的L为Ldrawn;
- Vth:阈值电压;
集成电路版图中的MOS
NMOS和PMOS组成反相器

- 剖面图
- NMOS管:
- 源漏极是N型材料,浅绿色的N+表示;
- 衬底电位由右边的P+提供;
- 栅极即红色ploy;
- PMOS管:
- 源漏极是P型材料,紫红色的P+表示;
- 衬底电位由左边浅绿色的N+提供;
- 栅极即红色ploy;
- 注意:在硅工艺中一般采用P型衬底,相当于总衬底,那么在PMOS管工艺中要先构建N-阱,再在上面做N+;
- NMOS管:
MOS管的工作状态及相关参数
- 以NMOS增强型为例
过程一(都接地)
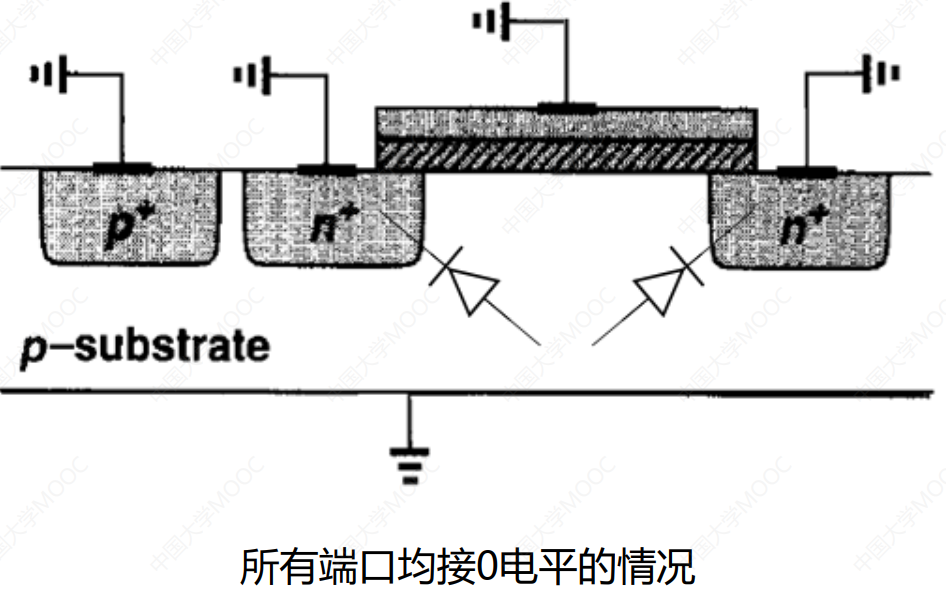
- MOS管处于截止状态,无导电沟道;
- 栅极下方是两个背靠背的反向PN结(相当于两个二极管);
过程二(形成耗尽层)
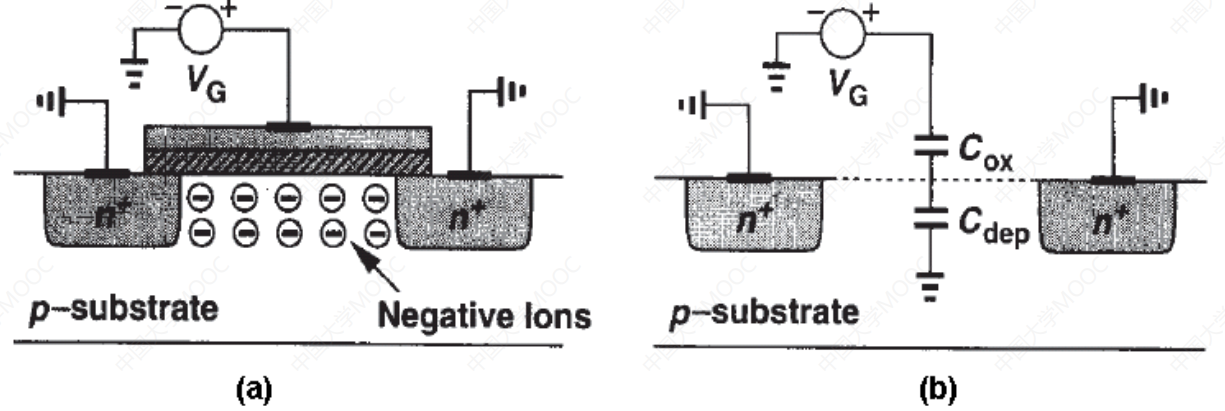
- 当0<VGS<VTH时,产生电场,并未形成导电沟道;
- 栅和衬底形成了电容,随着VG的增大,栅极上出现很多正电荷,从而使得P型衬底上的空穴远离栅极,留下负离子来镜像栅极上的正电荷——形成耗尽层;
- 栅极氧化层和耗尽层均不导电,表现为两个电容串联;
- Cox为固定电容;
- Cdep为可变电容;
过程三(形成反型层)
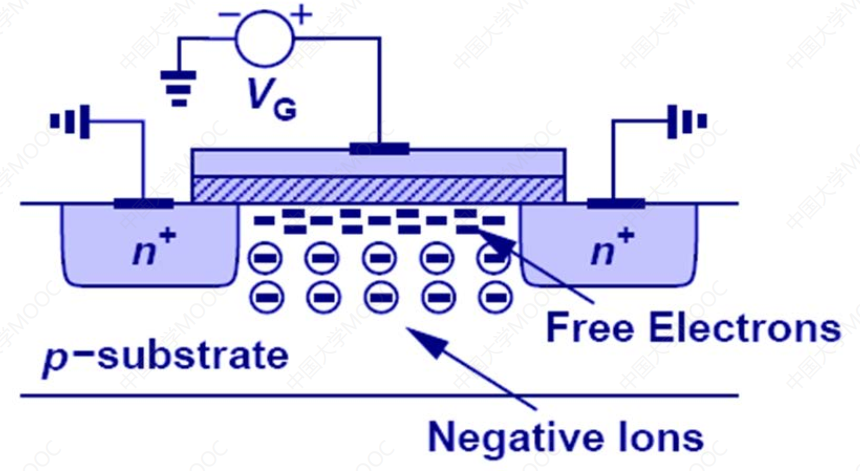
- 随着VG的进一步增加,界面电势达到一个足够高的值后,将吸引电子到栅极氧化层下方,以镜像栅极上更多的正电荷;
- 该电子是自由电子,在栅极下方形成导电“沟道”;
- 这块区域原先是P-substrate,现在变成了类似N型材料的特性,所以称为:反型层(inverted);
过程四(形成电流)
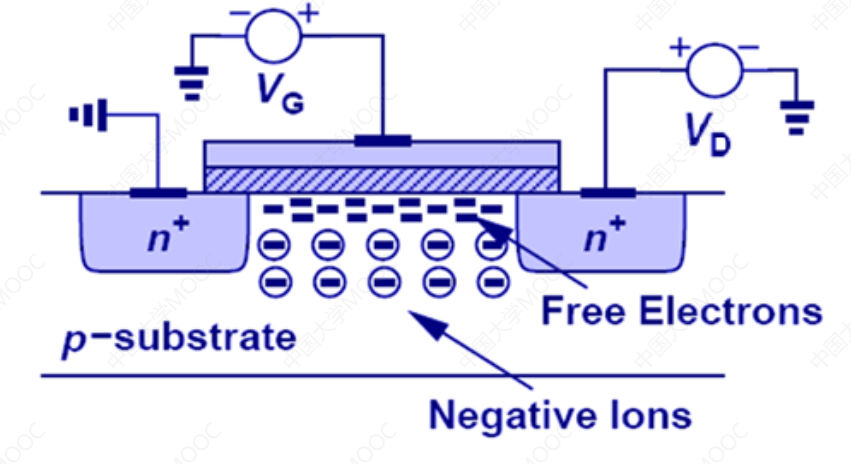
- 漏极和源极之间加入电压差,形成电流;
过程五(沟道夹断:进入饱和区)
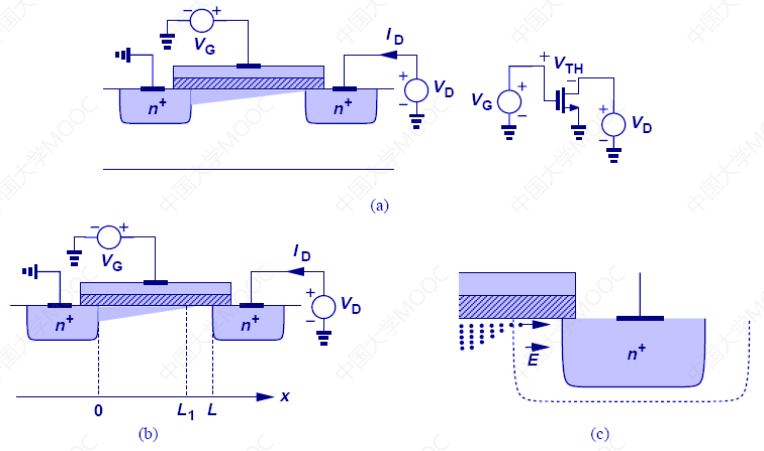
- 沟道长度变短,意味着沟道电荷变为0,出现了一个很强的横向电场,可以让电子快速通过;
- 此时漏源电流不再取决于夹断区电子的物理特性;
- 当VDS更大时,靠近漏级的反型层开始出现夹断;
- 当VD-VG=VTH时,靠近漏级的反型层完全被夹断;
- 当VD-VG>VTH时,由反型层构成的沟道长度开始变短;
过程六(饱和区)
- 当VDS>VGS-VTH,即VGD=VGS-VDS<VTH(阈值电压),这时漏端沟道不复存在。夹断时,沟道的平均横向电场不是依赖于漏源电压,而是沟道上的电压(VGS-VTH)。
- 此时,夹断区漏电流和VDS无关。实际上,夹断区的漏电流随着漏电压的改变而轻微的改变。
重要参数—阈值电压
- 阈值电压VTH:当出现反型层时对应的G与S之间的电压值。
- VTH的公式为: V T H = Φ M S + 2 Φ F + Q d e p C o x V_{TH}=Φ_{MS}+2Φ_{F}+\frac{Q_{dep}}{C_{ox}} VTH=ΦMS+2ΦF+CoxQdep
- Φ M S Φ_{MS} ΦMS:栅极与衬底之间的功函数差
- Φ F Φ_{F} ΦF:费米能级
- Q d e p Q_{dep} Qdep:耗尽区的电荷浓度
- C o x C_{ox} Cox:单位面积电容
- 说明:
- Φ F = ( k T / q ) l n ( N s u b / n i ) Φ_{F}=(kT/q)ln(N_{sub}/n_i) ΦF=(kT/q)ln(Nsub/ni)
- k k k:玻尔兹曼常数
- T T T:温度
- q q q:电子电荷
- N s u b N_{sub} Nsub:衬底掺杂浓度
- n i n_i ni:本征载流子浓度
- Q d e p = 4 q ε s i ∣ Φ F ∣ N s u b Q_{dep}=\sqrt{4qε_{si}|Φ_{F}|N_{sub}} Qdep=4qεsi∣ΦF∣Nsub
- 可见:对于NMOS而言,更高的衬底浓度对应了更高的阈值VTH;而温度上升,一般VTH下降(温度也影响了ni);
- Φ F = ( k T / q ) l n ( N s u b / n i ) Φ_{F}=(kT/q)ln(N_{sub}/n_i) ΦF=(kT/q)ln(Nsub/ni)
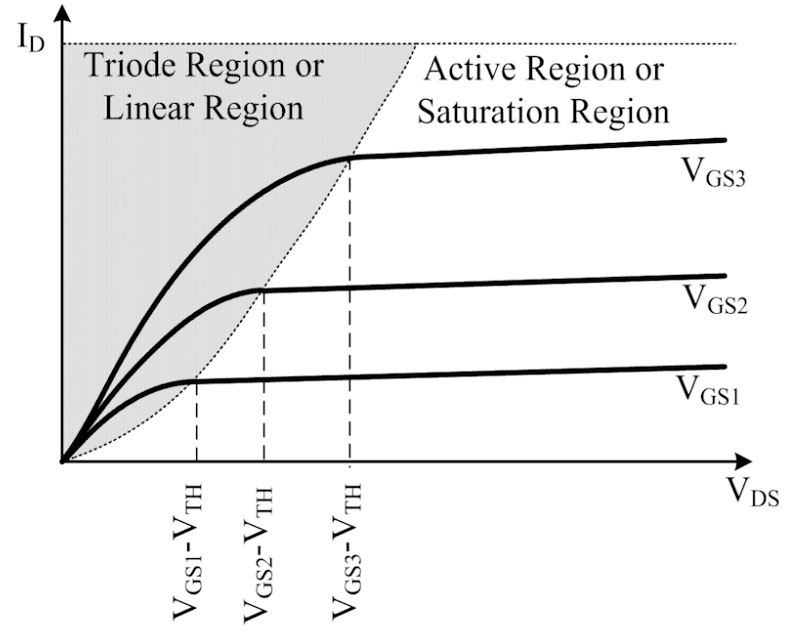
I/V特性曲线
电流密度与电荷密度的基本概念
- 电流 I:把导线看作一个管子,电流就是管子内定向行走的大量电子。电流在数值上等于导线管子垂直截面单位时间内通过的电子数量,即 I = d q d t I=\frac{dq}{dt} I=dtdq。
- 体电流密度 j:电流管子单位面积通过的电流,即电流管子单位时间单位横截面通过的电子数量(细品,你细品),即 j = d I d S j=\frac{dI}{dS} j=dSdI。
- 体电荷密度σe:单位体积内的电子数量,即 σ e = d q d V σ_e=\frac{dq}{dV} σe=dVdq。
- 如果导体内取一个圆柱体模型,长为dl,横截面dS,方向与电流方向一致,则: j = d I d S = d q d t d S = d q d l d t d S d l = d q d l d t d V = d l d t ∗ d q d V = u ∗ σ e j=\frac{dI}{dS}=\frac{dq}{dtdS}=\frac{dqdl}{dtdSdl}=\frac{dqdl}{dtdV}=\frac{dl}{dt}*\frac{dq}{dV}=u*σ_e j=dSdI=dtdSdq=dtdSdldqdl=dtdVdqdl=dtdl∗dVdq=u∗σe
- 其中u为dl/dt,即速度。
电流棒中的电流密度
- 要想搞清MOS管的I/V特性曲线,首先我们要明白电流密度(单位面积上电流的大小)、电荷面密度、与电流电压等关系。
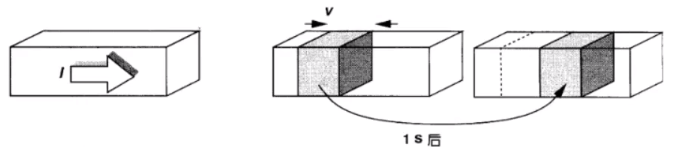
- 如上图的电流棒,当电荷密度为Qd的电荷以速度v沿着电流方向移动时,产生的电流密度为: J = Q d ∗ v J=Q_d*v J=Qd∗v(注意:这里是电流密度,而不是电流。)
NMOS管中未夹断时的电荷密度
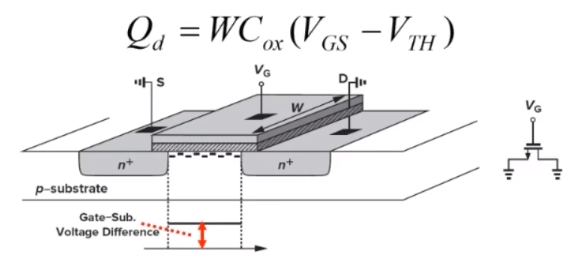
- 此时,MOS管中,未达到预夹断,电荷密度是均匀分布的,即可得线电荷密度为: Q d = W C o x ( V G S − V T H ) Q_d=WC_{ox}(V_{GS}-V_{TH}) Qd=WCox(VGS−VTH)
- 这里用到平行板电容器的公式: Q = C V Q=CV Q=CV;
- Cox为栅极单位面积电容,根据电容的并联可知W*Cox为电位长度栅电容,这个长度就是上图中根据反型层从左到右的一个区间。
- 到这一步应该就很容易理解了。
NMOS管中夹断时的电荷密度
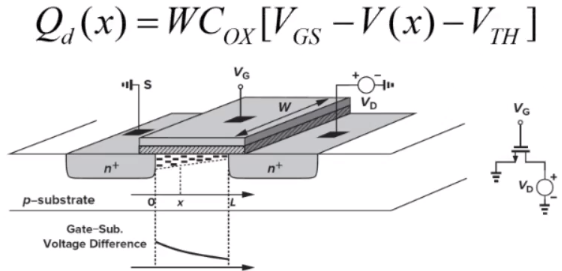
- 随着Vd的增大,此时电压为VDS出现夹断,可见位置x的不同,电荷密度也不相同。
- 此时, Q d = W C o x ( V G S − V T H − V ( x ) ) Q_d=WC_{ox}(V_{GS}-V_{TH}-V(x)) Qd=WCox(VGS−VTH−V(x))
构建等式(MOS管中的电流公式)
- 电荷漂移速度: v = μ E v=μE v=μE
- μ μ μ:迁移率 mobility
- v v v:漂移速度 drift speed
- E E E:电场强度 electric field
- 其中, E ( x ) = − d V ( x ) / d x E(x)=-dV(x)/dx E(x)=−dV(x)/dx
- 综上可得: I D = Q d ∗ v = Q d ∗ μ ∗ E ( x ) I_D=Q_{d}*v=Q_{d}*μ*E(x) ID=Qd∗v=Qd∗μ∗E(x),即 I D ( x ) = − W C o x [ V G S − V T H − V ( x ) ] ∗ μ n ∗ ( − d V ( x ) d x ) I_D(x)=-WC_{ox}[V_{GS}-V_{TH}-V(x)]*μ_n*(-\frac{dV(x)}{dx}) ID(x)=−WCox[VGS−VTH−V(x)]∗μn∗(−dxdV(x)) I D ( x ) = W C o x [ V G S − V T H − V ( x ) ] ∗ μ n ∗ d V ( x ) d x I_D(x)=WC_{ox}[V_{GS}-V_{TH}-V(x)]*μ_n*\frac{dV(x)}{dx} ID(x)=WCox[VGS−VTH−V(x)]∗μn∗dxdV(x)
- 给出边界条件: V ( 0 ) = 0 , V ( L ) = V D S V(0)=0, V(L)=V_{DS} V(0)=0,V(L)=VDS,两边积分可得: ∫ 0 L I D ( x ) d x = ∫ 0 V D S W μ n C o x [ V G S − V T H − V ( x ) ] d V ( x ) \int_{0}^{L}I_D(x)dx=\int_{0}^{V_{DS}}Wμ_nC_{ox}[V_{GS}-V_{TH}-V(x)]dV(x) ∫0LID(x)dx=∫0VDSWμnCox[VGS−VTH−V(x)]dV(x)
- 则有: I D = μ n C o x W L [ ( V G S − V T H ) V D S − 1 2 V D S 2 ] I_{D}=μ_nC_{ox}\frac{W}{L}[(V_{GS}-V_{TH})V_{DS}-\frac{1}{2}V^{2}_{DS}] ID=μnCoxLW[(VGS−VTH)VDS−21VDS2]
MOS管一级模型
- 公式说明
- μnCOX:MOS管的工艺参数;
- W/L:MOS管的宽长比;
- VTH:NMOS的阈值电压;
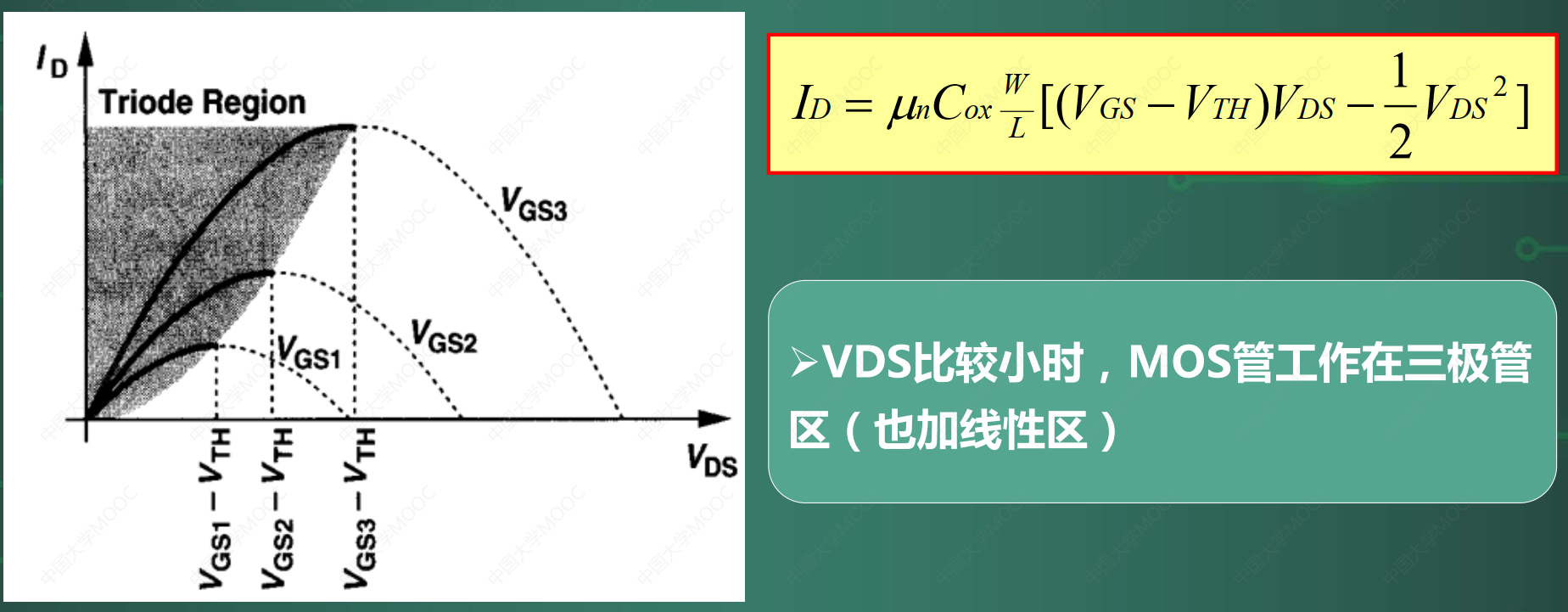
三极管区/可变电阻区
- VDS<VGS-VTH,器件工作在“三极管区”。
- MOS器件作为模拟开关或小值线性电阻运用时,都会工作在深Triode区(可变电阻区或深三极管区)。若满足 V D S < < 2 ( V G S − V T H ) V_{DS}<<2(V_{GS}-V_{TH}) VDS<<2(VGS−VTH)时,电流可化简为: I D ≈ μ n C o x W L ( V G S − V T H ) V D S I_{D}\approx μ_nC_{ox}\frac{W}{L}(V_{GS}-V_{TH})V_{DS} ID≈μnCoxLW(VGS−VTH)VDS
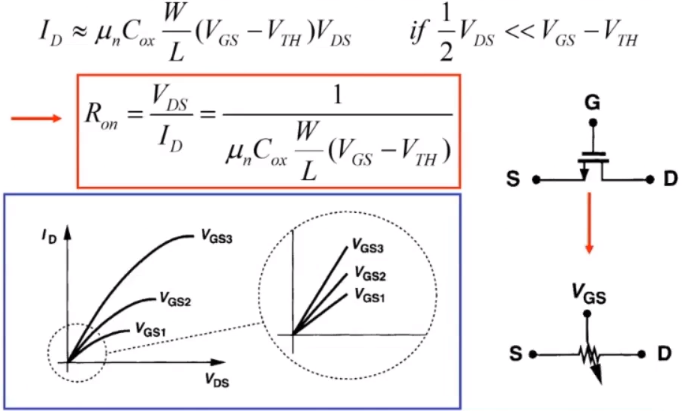
- 当VDS<<2(VGS-VTH)时,MOS管的I/V特性曲线近似为线性,对外等效为线性电阻,其交流动态电阻与直流电阻相等。
- 该线性电阻大小取决于VGS,即调节VGS,可调节电阻的大小。通常把工作在这种区域的晶体管称为“压控晶体管”。
过驱动电压
- 抛物线的极大值在 V D S = ( V G S − V T H ) V_{DS}=(V_{GS}-V_{TH}) VDS=(VGS−VTH)时,此时峰值电流为: I D − m a x = 1 2 μ n C o x W L ( V G S − V T H ) 2 I_{D-max}=\frac{1}{2}μ_nC_{ox}\frac{W}{L}(V_{GS}-V_{TH})^2 ID−max=21μnCoxLW(VGS−VTH)2
- 此时VGS-VTH为过驱动(overdrive)电压。
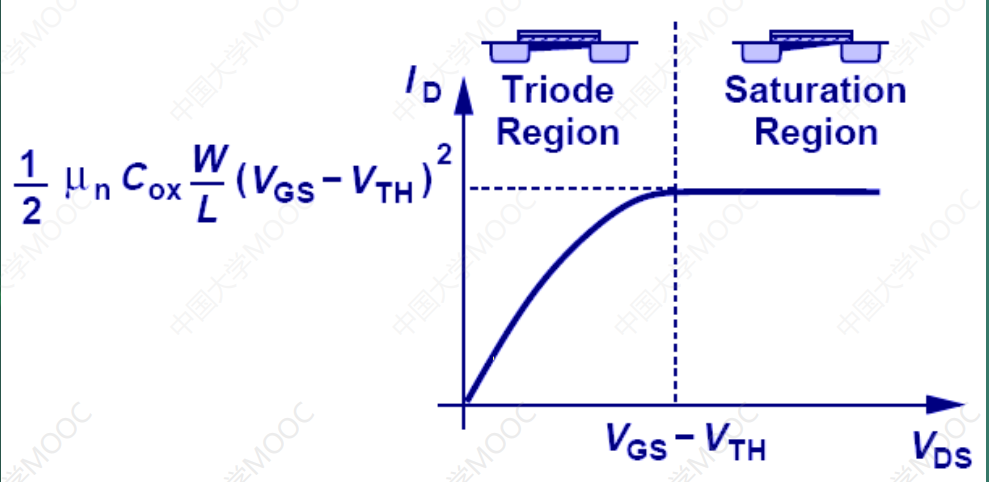
饱和区/恒流区
- 当VDS>VGS-VTH时,由Qd(x)=WCox(VGS-VTH-V(x))可知,V(x)=VGS-VTH时,Qd(x)=0,此时认为沟道夹断(pinch off)。
- VDS=VGS-VTH,沟道在x=L处夹断;
- VDS>VGS-VTH时,夹断点随着VDS的增大而向源极移动;
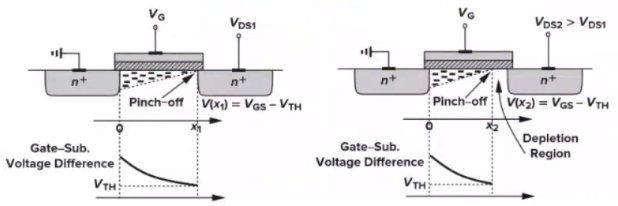
- 同理可得: I D = 1 2 μ n C o x W L ′ ( V G S − V T H ) 2 I_D=\frac{1}{2}μ_nC_{ox}\frac{W}{L'}(V_{GS}-V_{TH})^2 ID=21μnCoxL′W(VGS−VTH)2
- 若 L ′ ≈ L L'\approx L L′≈L,则 I D I_D ID与 V D S V_{DS} VDS无关。器件工作在饱和区(或恒流区)。
- 饱和后的MOS管相当于一个电流源:
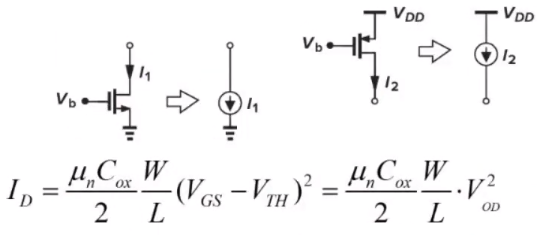
- 其中VOD就是过驱动电压,可推导得: V O D = V G S − V T H = 2 I D μ n C o x ( W / L ) V_{OD}=V_{GS}-V_{TH}=\sqrt{\frac{2I_D}{μ_nC_{ox}(W/L)}} VOD=VGS−VTH=μnCox(W/L)2ID
模拟CMOS设计最基本的方程式
I D = μ n C o x W L [ ( V G S − V T H ) V D S − 1 2 V D S 2 ] I_{D}=μ_nC_{ox}\frac{W}{L}[(V_{GS}-V_{TH})V_{DS}-\frac{1}{2}V^{2}_{DS}] ID=μnCoxLW[(VGS−VTH)VDS−21VDS2]
I D = 1 2 μ n C o x W L ′ ( V G S − V T H ) 2 I_D=\frac{1}{2}μ_nC_{ox}\frac{W}{L'}(V_{GS}-V_{TH})^2 ID=21μnCoxL′W(VGS−VTH)2
- 它们描述了 I D I_D ID与工艺常数 μ n C o x μ_nC_{ox} μnCox,器件尺寸W和L以及栅和漏相对于源的电位之间关系。
- 我自己加的: V O D = V G S − V T H = 2 I D μ n C o x ( W / L ) V_{OD}=V_{GS}-V_{TH}=\sqrt{\frac{2I_D}{μ_nC_{ox}(W/L)}} VOD=VGS−VTH=μnCox(W/L)2ID
合并两个I/V曲线
- 设 L ′ ≈ L L'\approx L L′≈L,合并两个电流曲线公式,可得: