一、扩展卡尔曼滤波

KF和EKF的公式对比（基本没差别）
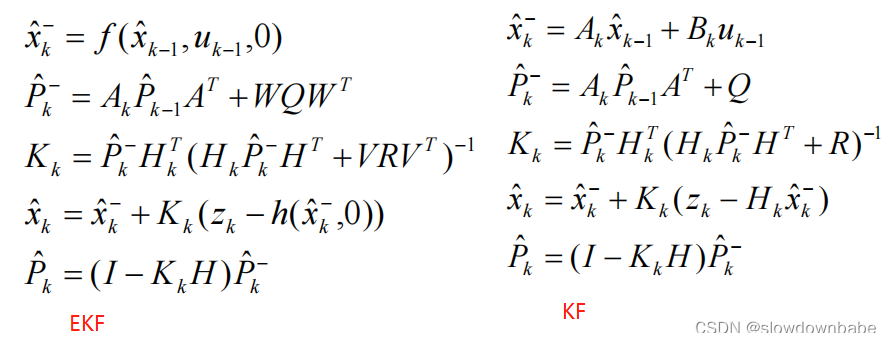
在这里插入图片描述

二、扩展卡尔曼五个公式

利用扩展卡尔曼滤波估计四元数。
下图是论文中的截图。可以和前面的卡尔曼滤波估计高度文章的那五个公式对应一下。
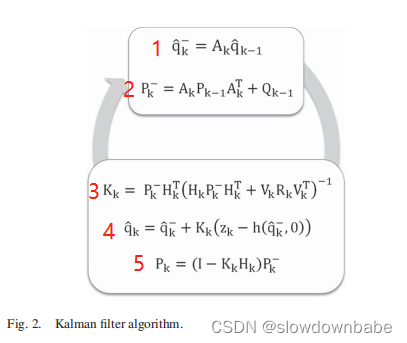
在这里插入图片描述
观测矩阵的确定。

三、代码的实现

1. 四元数模长归一化

static void NormalizeQuat(arm_matrix_instance_f32 *_q)
{float norm  = invSqrt(_q->pData[0] * _q->pData[0]  + _q->pData[1] * _q->pData[1] + _q->pData[2]*_q->pData[2] + _q->pData[3]*_q->pData[3]);// 归一化四元数_q->pData[0] *= norm;_q->pData[1] *= norm;_q->pData[2] *= norm;_q->pData[3] *= norm;
}

2. 快速开平方求导

// Fast inverse square-root
// See: http://en.wikipedia.org/wiki/Fast_inverse_square_root
float invSqrt(float x)	/*快速开平方求倒*/
{float halfx = 0.5f * x;float y = x;long i = *(long*)&y;i = 0x5f3759df - (i>>1);y = *(float*)&i;y = y * (1.5f - (halfx * y * y));return y;
}

3. EKF公式1,2

/* * 卡尔曼公式1,2--计算先验的_q_（四元数）和_P_（误差协方差矩阵）* 输入：机体角速度 w (rad/s), (3x1)* 			时间步长 dt (s)*			上一次后验的四元数 _q (4x1)
*			上一次后验的协方差矩阵 _P (4x4):这里和加速度计有关*			过程噪声协方差矩阵Q (4x4)* 输出：先验状态，四元数 _q_ (4x1)*			误差协方差矩阵的先验估计 _P_  (4x4)*/
static void Km12(const  Axis3f w, const float dt, const arm_matrix_instance_f32 _q, const arm_matrix_instance_f32 _P, const arm_matrix_instance_f32 _Q ,arm_matrix_instance_f32 _q_, arm_matrix_instance_f32 _P_)
{float32_t A[16];arm_matrix_instance_f32 _A;float32_t A_T[16] = {1,0,0,0, 0,1,0,0, 0,0,1,0, 0,0,0,1};		// 矩阵A的转置arm_matrix_instance_f32 _A_T;float32_t T[16] = {1,0,0,0, 0,1,0,0, 0,0,1,0, 0,0,0,1};		// 临时定义中间变量arm_matrix_instance_f32 _T;float32_t T2[16] = {1,0,0,0, 0,1,0,0, 0,0,1,0, 0,0,0,1};		// 临时定义中间变量arm_matrix_instance_f32 _T2;float temp;temp = dt / 2;A[0] = 1.0f; 			A[1] = -w.x*temp; 	A[2] = -w.y*temp; 	A[3] = -w.z*temp;A[4] = w.x*temp;	A[5] = 1.0f;				A[6] = w.z*temp;		A[7] = -w.y*temp;A[8] = w.y*temp;	A[9] = -w.z*temp;		A[10] = 1.0f;				A[11] = w.x*temp;A[12] = w.z*temp;	A[13]= w.y*temp;		A[14] = -w.x*temp;	A[15] = 1.0f;arm_mat_init_f32(&_A, 4, 4, A);				// 转移矩阵A (4x4)arm_mat_init_f32(&_A_T, 4, 4, A_T);arm_mat_init_f32(&_T, 4, 4, T);arm_mat_init_f32(&_T2, 4, 4, T2);arm_mat_trans_f32(&_A, &_A_T);				// A' (4x4)arm_mat_mult_f32(&_A, &_P, &_T);			// _T = _A*_P  (4x4)arm_mat_mult_f32(&_T, &_A_T, &_T2);		// _T2_ = _T*_A_T  (4x4)arm_mat_add_f32(&_T2, &_Q, &_P_); // _P_ = _T2 + _Q = _A*_P*_A_T + _Q;误差协方差矩阵的先验估计公式arm_mat_mult_f32(&_A, &_q, &_q_);			// q_ = A*q (4x1) xk的先验估计，没有控制项
}

4. EKF公式3

/** 卡尔曼公式3--计算卡尔曼增益* 输入：上一次估计四元数 _q (4x1)*			先验的误差协方差矩阵 _P_ (4x4)*			测量噪声协方差矩阵 _R (3x3)* 输出：卡尔曼增益 _K (4x3)*/
static void Km3(const arm_matrix_instance_f32 _q, const arm_matrix_instance_f32 _P_, const arm_matrix_instance_f32 _R, arm_matrix_instance_f32 _K)
{float32_t H[12];	// (3x4)float32_t H_T[12];  // (4x3)float32_t T[12];	// (3x4)float32_t T1[9];	// (3x3)float32_t M[9];		// (3x3)float32_t M_[9];	// M的逆, (3x3)arm_matrix_instance_f32 _H;arm_matrix_instance_f32 _H_T;arm_matrix_instance_f32 _T;arm_matrix_instance_f32 _T1;arm_matrix_instance_f32 _M;arm_matrix_instance_f32 _M_;// 用加速度计进行修正时的观测矩阵H[0] = -2*_q.pData[2];		H[1] =  2*_q.pData[3];			H[2] = -2*_q.pData[0];		H[3] =  2*_q.pData[1];H[4] =  2*_q.pData[1];		H[5] =  2*_q.pData[0];			H[6] =  2*_q.pData[3];		H[7] =  2*_q.pData[2];H[8] =  2*_q.pData[0];		H[9] = -2*_q.pData[1];			H[10] = -2*_q.pData[2];		H[11] =  2*_q.pData[3];// 矩阵初始化arm_mat_init_f32(&_H, 3, 4, H);				// 观测矩阵H (3x4)arm_mat_init_f32(&_H_T, 4, 3, H_T);arm_mat_init_f32(&_T, 3, 4, T);				// T (3x4)arm_mat_init_f32(&_M, 3, 3, M);				// M (3x3)arm_mat_init_f32(&_M_, 3, 3, M_);			// M_(3x3)arm_mat_init_f32(&_T1, 3, 3, T1);// 卡尔曼增益arm_mat_mult_f32(&_H, &_P_, &_T);			// _T = _H*_P_		(3x4)arm_mat_trans_f32(&_H, &_H_T);				// _H_T (4x3)arm_mat_mult_f32(&_T, &_H_T, &_T1);			// _T1 = _H*_P_*_H_T (3x3)arm_mat_add_f32(&_T1, &_R, &_M);			// _M = _H*_P_*_H_T + _R			(3x3)arm_mat_inverse_f32(&_M, &_M_);				// _M_ = inv(_H*_P_*_H_T + R)		 (3x3)arm_mat_init_f32(&_T, 4, 3, T);				// 将T初始化为 4x3 矩阵arm_mat_mult_f32(&_P_, &_H_T, &_T);			// _T = _P_ * _H_T (4x3)arm_mat_mult_f32(&_T, &_M_, &_K);			// _K = _P_ * _H_T * inv(_H*_P_*_H_T + R);  (4x3)
}

5. EKF公式4,5

/** 卡尔曼公式4,5* 输入：观测的状态 a (加速度单位为 N/s^2） (3x1)*			先验的四元数 _qi (4x1)*      	上一次估计的 _q*			先验的噪声协方差矩阵 _P_*			卡尔曼增益 _K (4x3)* 输出：后验的四元数 _qo (4x1)*			后验的噪声协方差矩阵 _P (4x4)*/
static void Km45( const Axis3f a, const arm_matrix_instance_f32 _qi, const arm_matrix_instance_f32 _q, const arm_matrix_instance_f32 _P_, const arm_matrix_instance_f32 _K, arm_matrix_instance_f32 _qo, arm_matrix_instance_f32 _P)
{float norm 	; 			// 模长float32_t z[3];			// 观测的向量float32_t h[3];			// 地球系向量在机体系下的分量 (3x1)float32_t v3[3];		// 临时向量 (3x1)float32_t v4[4];		// 临时向量（4x1）float32_t I[16]= {1,0,0,0,  0,1,0,0,  0,0,1,0,  0,0,0,1};		// 单位阵（4x4）float32_t H[12];float32_t T[16];float32_t M[16];arm_matrix_instance_f32 _z;arm_matrix_instance_f32 _h;arm_matrix_instance_f32 _v3;arm_matrix_instance_f32 _v4;arm_matrix_instance_f32 _I ;arm_matrix_instance_f32 _H;arm_matrix_instance_f32 _T;arm_matrix_instance_f32 _M;// 获取测量值z[0] = a.x;z[1] = a.y;z[2] = a.z;// 矩阵初始化arm_mat_init_f32(&_z, 3, 1, z);arm_mat_init_f32(&_h, 3, 1, h);arm_mat_init_f32(&_v3, 3, 1, v3);arm_mat_init_f32(&_v4, 4, 1, v4);arm_mat_init_f32(&_I, 4, 4, I);arm_mat_init_f32(&_H, 3, 4, H);arm_mat_init_f32(&_T, 4, 4, T);arm_mat_init_f32(&_M, 4, 4, M);norm  = invSqrt(a.x*a.x + a.y*a.y + a.z * a.z);z[0] *= norm;z[1] *= norm;z[2] *= norm;h[0] = 2*_q.pData[1]*_q.pData[3] - 2*_q.pData[0]*_q.pData[2];h[1] = 2*_q.pData[0]*_q.pData[1] + 2*_q.pData[2]*_q.pData[3];h[2] = _q.pData[0]*_q.pData[0] - _q.pData[1]*_q.pData[1] - _q.pData[2]*_q.pData[2] + _q.pData[3]*_q.pData[3]; // 观测矩阵H[0] = -2*_q.pData[2];		H[1] =  2*_q.pData[3];			H[2] = -2*_q.pData[0];		H[3] =  2*_q.pData[1];H[4] =  2*_q.pData[1];		H[5] =  2*_q.pData[0];			H[6] =  2*_q.pData[3];		H[7] =  2*_q.pData[2];H[8] =  2*_q.pData[0];		H[9] = -2*_q.pData[1];			H[10] = -2*_q.pData[2];		H[11] =  2*_q.pData[3];// 修正qarm_mat_sub_f32(&_z, &_h, &_v3);		// _v3 = _z - _h  (3x1)arm_mat_mult_f32(&_K, &_v3, &_v4);		// _v4 = _K*(_z-_h)  (4x1)_v4.pData[3] = 0;						// 加速度计修正，不改变 q3。arm_mat_add_f32(&_qi, &_v4, &_qo);		// _qo = _qi + _v4 (4x4)// 修正Parm_mat_mult_f32(&_K, &_H, &_T);		// _T = _K*_H  (4x4)arm_mat_sub_f32(&_I, &_T, &_M);			// _M = _I - _K*_H (4x4)arm_mat_mult_f32(&_M, &_P_, &_P);		// _P = (_I - _K*_H) * _P_
}

6. 应用扩展卡尔曼滤波进行6自由度的姿态解算

/** 卡尔曼滤波姿态估计* 输入：六轴传感器数据 ，加速度 m/s^2, 加速度 rad/s,* 此函数将更新全局变量  姿态四元数 quat_ 与 欧拉角 eular_*/
void ekfdof6(Axis3f acc, Axis3f gyro, state_t *state , float dt)
{float accBuf[3] = {0.f};Axis3f tempacc = acc;// 必须进行转换，否则微小的变动就会导致姿态变化很大。gyro.x = gyro.x * DEG2RAD;	/* 度转弧度 */gyro.y = gyro.y * DEG2RAD;gyro.z = gyro.z * DEG2RAD;/* 卡尔曼滤波相关矩阵		*/static float32_t Q[16] = {1e-5f,0,0,0,   0,1e-5f,0,0,  0,0,1e-5f,0,  0,0,0,1e-5f};	// 过程噪声协方差矩阵 4X4static float32_t R[9] = {1,0,0,  0,1,0,    0,0,1};	// 加速度计测量噪声协方差矩阵static float32_t q[4] = {1, 0, 0, 0};	// 使用加速度计后验得到的协方差矩阵static float32_t q_[4] = {1, 0, 0, 0};	// 先验的qstatic float32_t P_[16] = {1,0,0,0, 0,1,0,0, 0,0,1,0, 0,0,0,1};	// 先验的误差协方差矩阵的值static float32_t P1[16] = {1,0,0,0, 0,1,0,0, 0,0,1,0, 0,0,0,1}; // 通过加速度计后验得到的误差协方差矩阵static float32_t K[12];		// 卡尔曼增益/* 指向卡尔曼滤波相关矩阵的指针	*/static arm_matrix_instance_f32 _Q;static arm_matrix_instance_f32 _R;static arm_matrix_instance_f32 _q;  // xk的后验估计static arm_matrix_instance_f32 _q_; // xk的先验估计static arm_matrix_instance_f32 _P_; // 误差协方差矩阵的先验估计static arm_matrix_instance_f32 _P1;static arm_matrix_instance_f32 _K;static uint16_t km_atti_times = 0;/* 初始化卡尔曼滤波相关矩阵			*/if (km_atti_times == 0){arm_mat_init_f32(&_Q, 4, 4, Q);arm_mat_init_f32(&_R, 3, 3, R);arm_mat_init_f32(&_q, 4, 1, q);arm_mat_init_f32(&_q_, 4, 1, q_);arm_mat_init_f32(&_P_, 4, 4, P_);arm_mat_init_f32(&_P1, 4, 4, P1);arm_mat_init_f32(&_K, 4, 3, K);km_atti_times = 1;}else if (km_atti_times < 1000)	// 先信任加速度计，收敛快{Q[0] = 8e-3f;Q[5] = 8e-3f;Q[10] =8e-3f;Q[15] = 8e-3f;km_atti_times ++;}else						// 后信任陀螺仪，准确{Q[0] = 1e-7f;Q[5] = 1e-7f;Q[10] = 1e-7f;Q[15] = 1e-7f;		}/* 卡尔曼滤波过程	*/Km12(gyro, dt, _q, _P1, _Q, _q_, _P_);			// 卡尔曼公式1,2 根据陀螺仪预测Km3(_q, _P_, _R, _K);							// 卡尔曼公式3，计算卡尔曼增益Km45(acc, _q_, _q, _P_, _K, _q, _P1);		   // 卡尔曼公式4,5 根据加速度修正NormalizeQuat(&_q);							 // 四元数归一化/* 赋值给全局变量 */q0 = _q.pData[0];									q1 = _q.pData[1];q2 = _q.pData[2];q3 = _q.pData[3];imuComputeRotationMatrix();	/*计算旋转矩阵*//*计算roll pitch yaw 欧拉角*/state->attitude.pitch = -asinf(rMat[2][0]) * RAD2DEG; state->attitude.roll = atan2f(rMat[2][1], rMat[2][2]) * RAD2DEG;state->attitude.yaw = atan2f(rMat[1][0], rMat[0][0]) * RAD2DEG;if (!isGravityCalibrated)	/*未校准*/{		accBuf[2] = tempacc.x* rMat[2][0] + tempacc.y * rMat[2][1] + tempacc.z * rMat[2][2];/*accz*/calBaseAcc(accBuf);		/*计算静态加速度*/				}
}

7. 计算旋转矩阵

/*计算旋转矩阵*/
void imuComputeRotationMatrix(void)
{float q1q1 = q1 * q1;float q2q2 = q2 * q2;float q3q3 = q3 * q3;float q0q1 = q0 * q1;float q0q2 = q0 * q2;float q0q3 = q0 * q3;float q1q2 = q1 * q2;float q1q3 = q1 * q3;float q2q3 = q2 * q3;rMat[0][0] = 1.0f - 2.0f * q2q2 - 2.0f * q3q3;rMat[0][1] = 2.0f * (q1q2 + -q0q3);rMat[0][2] = 2.0f * (q1q3 - -q0q2);rMat[1][0] = 2.0f * (q1q2 - -q0q3);rMat[1][1] = 1.0f - 2.0f * q1q1 - 2.0f * q3q3;rMat[1][2] = 2.0f * (q2q3 + -q0q1);rMat[2][0] = 2.0f * (q1q3 + -q0q2);rMat[2][1] = 2.0f * (q2q3 - -q0q1);rMat[2][2] = 1.0f - 2.0f * q1q1 - 2.0f * q2q2;
}

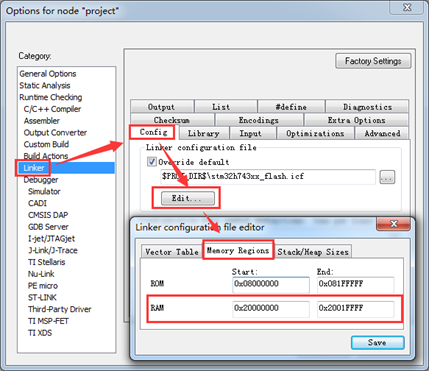
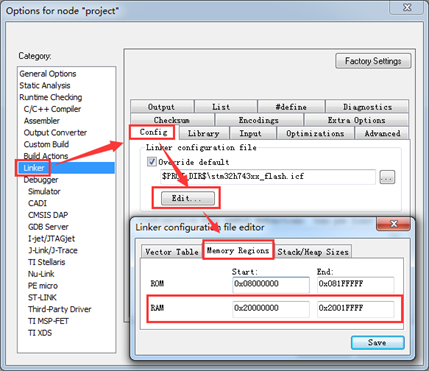
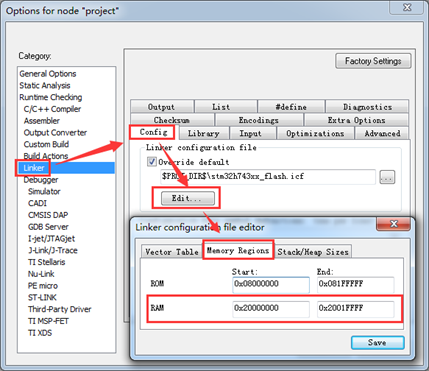
四、移植到MiniFly微型四轴中

6 , MiniFly V1.5\1，MiniFly Master\2，STM32F411\Firmware_F411 V1.4(改灯\FLIGHT\src\stabilizer.c

		//四元数和欧拉角计算（250Hz）if (RATE_DO_EXECUTE(ATTITUDE_ESTIMAT_RATE, tick)){
//			imuUpdate(sensorData.acc, sensorData.gyro, &state, ATTITUDE_ESTIMAT_DT);ekfdof6(sensorData.acc, sensorData.gyro, &state, ATTITUDE_ESTIMAT_DT); }