1 引言

本文采用手稿模拟的角度，尽量使读者较为直白的面对冷冰冰的公式。
抛去CW算法不谈。一般来说，生成样本算法都要保证如下两个条件：

• 1、对抗样本和干净样本的差距应该越小越好。评价指标有 L0，L2，L正无穷
• 2、对抗样本应该使得模型分类错，且分类错的那一类的置信度应足够的高（有目标攻击）。

条件一，保证了生成样本与原始干净样本尽量的相似。
条件二，保证了生成样本确实能成功攻击模型。
仔细想想，这两个条件是不是就满足了生成样本的全部需求哩。

问题定义清楚了，那问题的数学描述就成了关键。

2 算法详解

2.1 常人思路

数学描述：

• 上述公式，Rn满足了条件一，f (An) 满足了条件二。
• 由于是有目标攻击，t 就是我们想要攻击成的类别，表示将对抗样本输入模型后，它的softmax层第t个的值越大，也就说明模型将其归为第t个类别，攻击成功。
• 我们希望模型将其归为第t个类别的概率越大越好，也就是希望 Z(An)t 越大越好 。Z(An)t 前面加个负号，变为最小化问题。

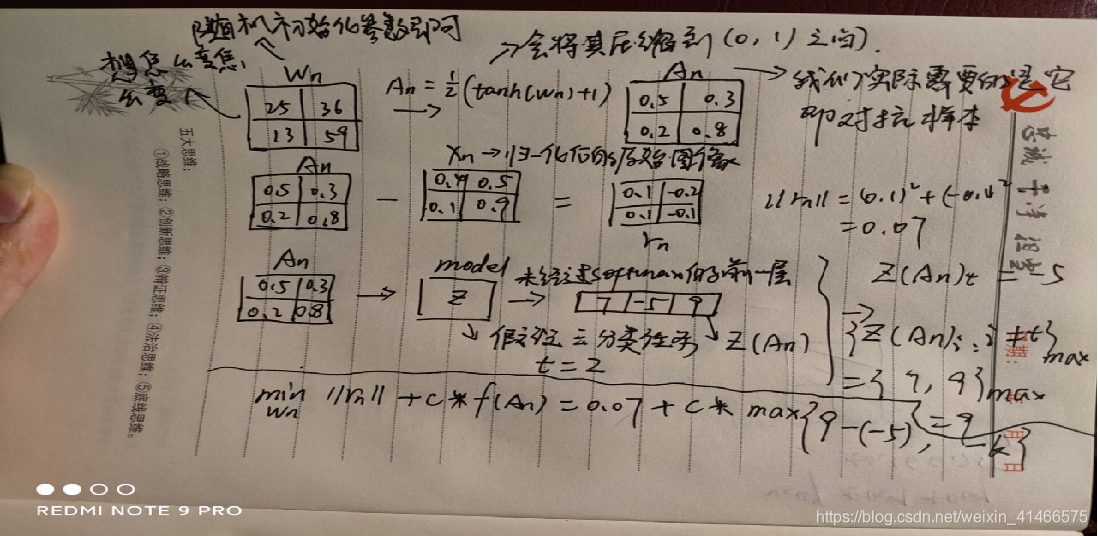
其手稿模拟如下：
如上的公式是不是很简单阿。那是我等常人的思考过程，肯定简单阿。但这并不是CW算法，它主要在此基础上做了优化，不然怎么发顶会呢。

• 我们常人思路的缺点：通过如上公式反向传播，An实际有可能超出像素范围。
• 办法一：使用截断的思想，但会使攻击性能下降
• 办法二：CW算法提出的思想，将其映射到tanh空间

2.2 CW算法思路

• 便于对比，CW算法与常人思路放在一起。
  
• 与之前不一样，它将An映射到了区间【0，1】，目的就是随便参数Wn怎么变，反正经过映射变换后，对抗样本An也不会超出像素点的范围。
• 现在我们将类别 t（也就是我们最后想要攻击成的类别）所对应的逻辑值记为 Z(An)t，将最大的值（对应类别不同于t）记为 max{Z(An)i : i!=t }，如果通过优化使得max{Z(An)i : i!=t } - Z(An)t变小，攻击不就离成功了更近嘛。

CW算法手稿模拟：

这里你可能对如下图。为什么外面还要套个max，然后与-k这个超参数进行比较：

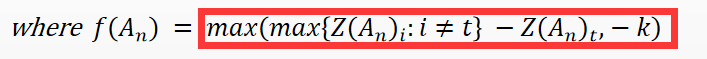
来张函数图，你感受下：

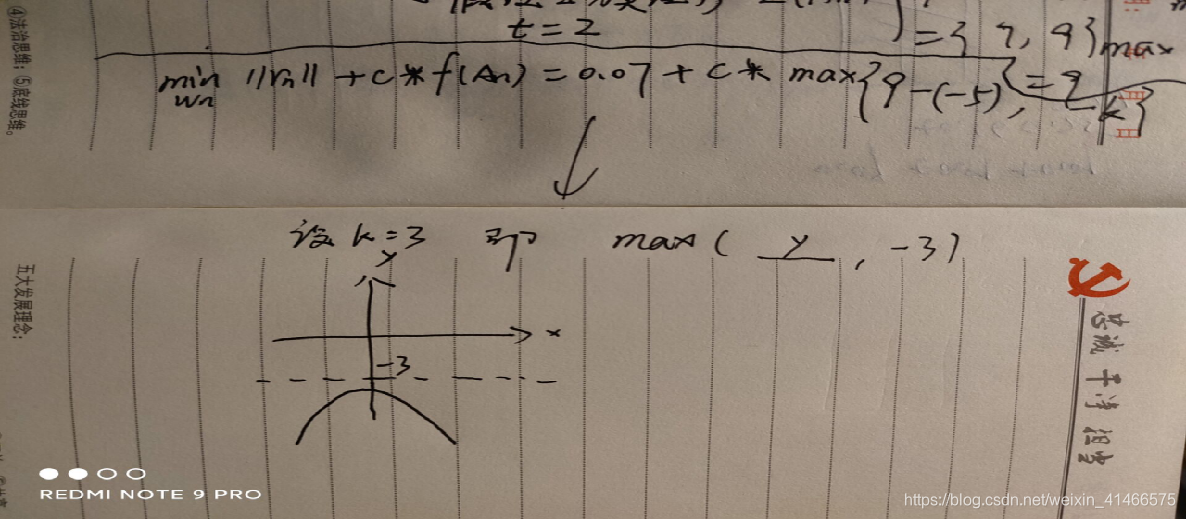
• 如上图，如果y的值（即损失值），比 -k 要小，那max( y , -3 )的值就一直是 -3 ，即使继续反向传播也不会优化参数了。
• 我认为这一步加得鸡肋。给我一种感觉：你在不断努力地内卷，然后有个人不断的跟你说，你足够好了，不要学了，不要学了！！！
• 因此可以理解为，k越大，那么模型分错，且错成的那一类的概率越大。

3 攻击直观对比

常人思路攻击：
CW攻击：

4 总结

CW是一个基于优化的攻击，主要调节的参数是c和k,看你自己的需要了。它的优点在于，可以调节置信度，生成的扰动小，可以破解很多的防御方法，缺点是，很慢。

5 附录

• 论文：

• CW攻击原论文地址——https://arxiv.org/pdf/1608.04644.pdf

• 代码：

• 作者github代码：https://github.com/carlini/nn_robust_attacks/blob/master/l2_attack.py

• 本人代码：https://colab.research.google.com/drive/1Lc36RwSqvbLTxY6G6O1hkuBn9W49x0jO?usp=sharing

• 博客：

• CW算法详解–https://www.cnblogs.com/tangweijqxx/p/10627360.html

欢迎留言，力所能及，必答之。

关注我，带你体验不一样的AI生活。