基于spss的多元统计分析之因子分析（4/8）

实验目的：

1．掌握因子分析的基本思想；

2．熟悉掌握SPSS软件进行因子分析的基本操作；

3．利用实验指导的实例数据，上机熟悉因子分析方法。

实验内容：

附表的数据来自一次对液晶电视的调查。在这次调查中，被调查者回答了关于电视机音响效果、画面清晰度、画面色彩、外观效果、性价比和操作方便性等几个方面对于购买决策是否重要的问题。如果被调查者认为自己在购买电视机时非常注重某个方面，则打5分，比较注重打4分，注重程度一般打3分，不太注重打2分，非常不注重打1分。下面的数据适合做因子分析吗？如果适合，请进行因子分析，并对分析的结果进行解释。

实验前预习：

主成分分析的基本思想；

SPSS软件进行主成分分析的基本操作；

程序测试、运行结果及分析：

因子分析

操作步骤：

打开spss软件，输入相关数据 à 在“变量视图”更改名称 à 点击“分析”à 点击“描述统计” à 选择“描述” à 点击“将标准化数值另存为变量”并点击“确定”à点击“分析”à点击“降维” à 选择“因子分析”à拖动标准化后的变量拖至变量框 à 点击“描述”选择KMO和“系数”à点击提取选择“主成分”和“碎石图”à 点击旋转选择“最大方差法”à 点击得分选择“保存为变量”à 点击“继续”和“确定”

运行结果及分析：

相关性矩阵
		X1	X2	X3	X4	X5	X6
相关性	X1	1.000	-.161	.524	.556	.210	-.054
	X2	-.161	1.000	-.144	-.044	.126	.042
	X3	.524	-.44	1.000	.411	.185	.000
	X4	.556	-.044	.411	1.000	-.001	-.122
	X5	.210	.126	.185	-.001	1.000	.559
	X6	-.054	.042	.000	-.122	.559	1.000

X1，X2，X3、X4、X5、X6，分别代表、画面清晰度、

给出相关系数矩阵，可以看出，一些变量的相关程度较小。

KMO 和巴特利特检验
KMO 取样适切性量数。		.575
巴特利特球形度检验	近似卡方	59.974
	自由度	15
	显著性	.000

0.575较小，可能得出的的因子分析模型不太理想，0.00表示各个变量存在相关性。

公因子方差
	初始	提取
Zscore(音响效果)	1.000	.749
Zscore(画面清晰度)	1.000	.123
Zscore(画面色彩)	1.000	.624
Zscore(外观效果)	1.000	.621
Zscore(性价比)	1.000	.810
Zscore(操作方便)	1.000	.748
提取方法：主成分分析法。

提取列数据表示为公共因子解释其余变量的方差的比例，即各变量含有原始变量的信息能被提取的公因子代表程度，0.123说明提取的公因子对该变量的代表性是很差的。

总方差解释
成分	初始特征值			提取载荷平方和			旋转载荷平方和
成分	总计	方差百分比	累积 %	总计	方差百分比	累积 %	总计	方差百分比	累积 %
1	2.076	34.601	34.601	2.076	34.601	34.601	2.069	34.483	34.483
2	1.598	26.639	61.240	1.598	26.639	61.240	1.605	26.757	61.240
3	.976	16.270	77.510
4	.564	9.399	86.909
5	.463	7.713	94.622
6	.323	5.378	100.000
提取方法：主成分分析法。

表明各因子的方差贡献率和累计贡献率。

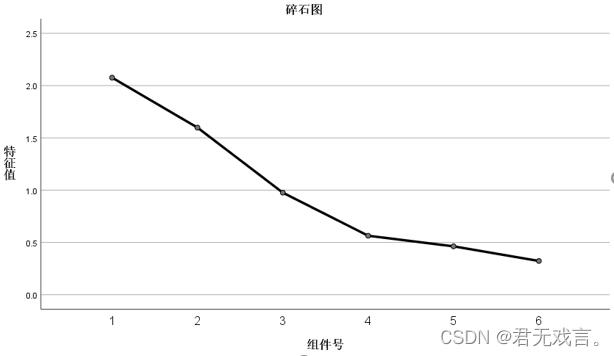
特征值反应变量的重要程度。

旋转后的成分矩阵a
	成分
	1	2
Zscore(音响效果)	.863	.068
Zscore(画面清晰度)	-.263	.232
Zscore(画面色彩)	.782	.113
Zscore(外观效果)	.778	-.127
Zscore(性价比)	.175	.883
Zscore(操作方便)	-.097	.859
提取方法：主成分分析法。旋转方法：凯撒正态化最大方差法。
a. 旋转在 3 次迭代后已收敛。

结果表示第一个因子在音响效果和画面色彩以及外观效果上有较大的载荷，因此第一个因子为电视机的性能效果因子。而第二个因子在性价比和操作方便上有较大载荷，所以第二个因子为电视机的实用性效果因子。

最终得到公式：X1=0.863*F1+0.068*F2，X1=-0.263*F1+0.232*F2…..

主成分中是按列写出各个主成分公式，但是在因子分析中是按行看，表示各因子在各变量上的载荷（各因子对各变量的影响程度）

成分得分系数矩阵
	成分
	1	2
Zscore(音响效果)	.416	.027
Zscore(画面清晰度)	-.131	.149
Zscore(画面色彩)	.376	.057
Zscore(外观效果)	.378	-.093
Zscore(性价比)	.069	.547
Zscore(操作方便)	-.062	.538

由得分系数矩阵可知：

F1=0.416*x1-0.131*x2+0.376*x3+0.378*x4+0.069*x5-0.062*x6，

F2略。

软件自动保存变量，数据视图中给出了各因子得分，默认变量名为FAC1_1、FAC2_1、FAC3_1。在数字表达式中输入34.483 / 61.240*FAC1_1+26.757/61.240*FAC2_1得到结果后右键数据列选择降序排序得到表格：

编号	性能因子	实用因子	综合得分	编号	性能因子	实用因子	综合得分
3	0.96224	1.67526	1.27	16	-0.02016	0.06915	0.02
41	1.31957	0.82926	1.11	5	0.09076	-0.09792	0.01
38	0.57533	1.76999	1.1	48	0.31668	-0.39976	0
13	0.03342	2.36644	1.05	33	0.08707	-0.13875	-0.01
42	0.73404	1.30909	0.99	12	-0.32449	0.28931	-0.06
4	1.392	0.2021	0.87	31	-0.86641	0.88577	-0.1
25	1.52236	0.0337	0.87	6	0.00449	-0.26419	-0.11
14	0.10584	1.73928	0.82	19	0.00079	-0.30502	-0.13
15	-0.41142	2.0024	0.64	22	-0.08179	-0.43045	-0.23
45	1.33407	-0.25667	0.64	11	0.49217	-1.27858	-0.28
23	1.46443	-0.42507	0.64	49	-1.02741	0.67865	-0.28
46	0.94716	-0.16194	0.46	35	0.07692	-0.89135	-0.35
47	0.99113	-0.29674	0.43	37	-0.59905	-0.16733	-0.41
39	-0.10938	1.11423	0.43	7	-0.30999	-0.79662	-0.52
20	-0.88091	1.9717	0.37	30	-0.85191	-0.20016	-0.57
44	0.86089	-0.32821	0.34	27	0.01899	-1.35012	-0.58
40	-0.18029	0.91434	0.3	50	-0.16296	-1.18307	-0.61
43	0.24795	0.26823	0.26	8	-0.78318	-0.86816	-0.82
34	1.01959	-0.78911	0.23	9	-0.78318	-0.86816	-0.82
1	2.0374	-2.12564	0.22	10	-0.78318	-0.86816	-0.82
24	0.60433	-0.40187	0.16	36	-1.70831	-0.13614	-1.02
21	0.06242	0.19458	0.12	28	-0.92368	-1.45236	-1.15
26	0.06242	0.19458	0.12	17	-2.51417	0.30499	-1.28
32	0.80296	-0.78698	0.11	29	-1.31059	-1.35763	-1.33
18	-0.35284	0.58181	0.06	2	-3.18209	-0.76869	-2.13

讨论：

1.主成分分析和因子分析的区别

（1）因子分析需要构造因子模型，着重要求新变量，具有实际的意义，能解释原始变量间的内在结构。

（2）主成分分析仅仅是变量变换，是原始变量的线性组合表示新的综合变量，强调新变量贡献了多大比例的方差，不关心新变量是否有明确的实际意义。两者都是降维和信息浓缩的方法，生成的新变量均代表了原始变量的大部分信息且互相独立，都可以用于后续的回归分析、判别分析、聚类分析等等。

2.主成分分析和因子分析的基本原理

主成分分析基本原理：利用降维（线性变换)的思想，在损失很少信息的前提下把多个指标转化为几个不相关的综合指标（主成分),即每个主成分都是原始变量的线性组合,且各个主成分之间互不相关,使得主成分比原始变量具有某些更优越的性能（主成分必须保留原始变量90%以上的信息），从而达到简化系统结构，抓住问题实质的目的。

因子分析基本原理：利用降维的思想，由研究原始变量相关矩阵内部的依赖关系出发，把一些具有错综复杂关系的变量表示成少数的公共因子和仅对某一个变量有作用的特殊因子线性组合而成。就是要从数据中提取对变量起解释作用的少数公共因子（因子分析是主成分的推广，相对于主成分分析，更倾向于描述原始变量之间的相关关系）。

2.总结

因子分析就是研究如何以最少的信息丢失将众多原有变量浓缩成少数几个因子，以较少几个因子来反映原始变量的大部分信息的统计学分析方法。它的基本思想是将原始变量分类，将相关性较高的变量分在同一类，而不同类的变量之间相关性较低，那么每一类变量实际上就代表了一个基本结构，即公共因子。