布洛赫波函数
整体的思想还是基于建模,大家应该都知道在自由电子模型中,能量和波矢的关系
那么大家的第一个疑问首先是,空间结构的周期性应该反应在空间坐标上,为什么K空间也会满足周期性呢?
这里面就不得不说,K空间的建立,着实是精彩:
它将平常大家所理解的三维空间和波矢空间(倒空间完美的结合在了一起),并且其满足一一对应的关系,因此三维空间中存在周期性,倒空间也必然存在周期性,倒空间可以看作是三维空间的一个等价描述(大家可以试着抛弃原先狭隘的时空观念)
其次第二个困惑是,我们如何建立关于周期性的条件,来约束电子的运动呢?并且还要完美的符合之前布拉格衍射的条件?
这里就要感谢布洛赫所做的工作:
布洛赫定理———对于考虑周期性势场的薛定谔方程,其解必定具有如下的特殊形式
,这就是布洛赫波函数
其中是具有晶体点阵的周期,即
由此我们周期性条件的方程就建立完成了
关于布洛赫函数,其中有三个需要记住的点:
1. 下标K指明函数依赖于波矢k
2. 布洛赫函数可以由行波组成,他们叠加后可以成为波包,从而表示在离子实势场中自由传播的电子
3. k的值出现在晶体中电子碰撞过程的守恒定律之中,因此称为电子的晶体动量
克朗尼格-朋奈模型
一维周期性方阱势场 是势能,
是能量本征值
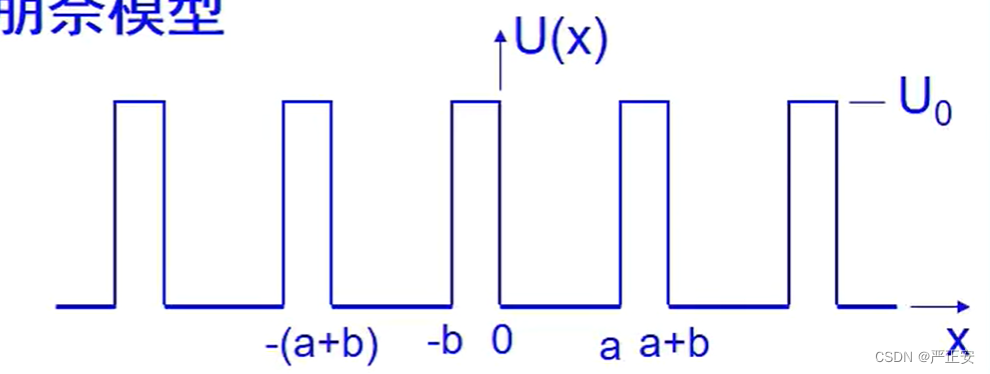
其中势场满足这个条件
因为正电荷吸引负电荷所造成的势场,相当于是向下掉,但是这样不好求解,我们做一个等价变换,把下面的陷阱翻上来,变成一个正值,所以,我们等于把势阱问题变成了势垒的问题,每一个势垒就是离子实所在的位置
我们可以列出通解方程
为了解这个方程,我们需要边界条件
1.连续性条件,和
在
处连续
2. 由布洛赫定义知道 和
在
处的值等于
处的值,但超前一个位相因子
所以四个条件往里面一带,我们就可以求出来
因此我们就得出了能量的解的形式
如果方程要有解我们,根据行列式不为0这个条件,我们还可以列出
只有上述关系式满足的时候,方程组才有解
为了简化结果,取的极限,同时保持
为一个有限量,约化后的关系式为
,只要这个方程满足,A,B,C,D一定有解
K是待定系数里的,k是布洛赫波函数里的真实波矢
能隙的出现
我们以等式的左右两边为函数,分别画图,可以得到
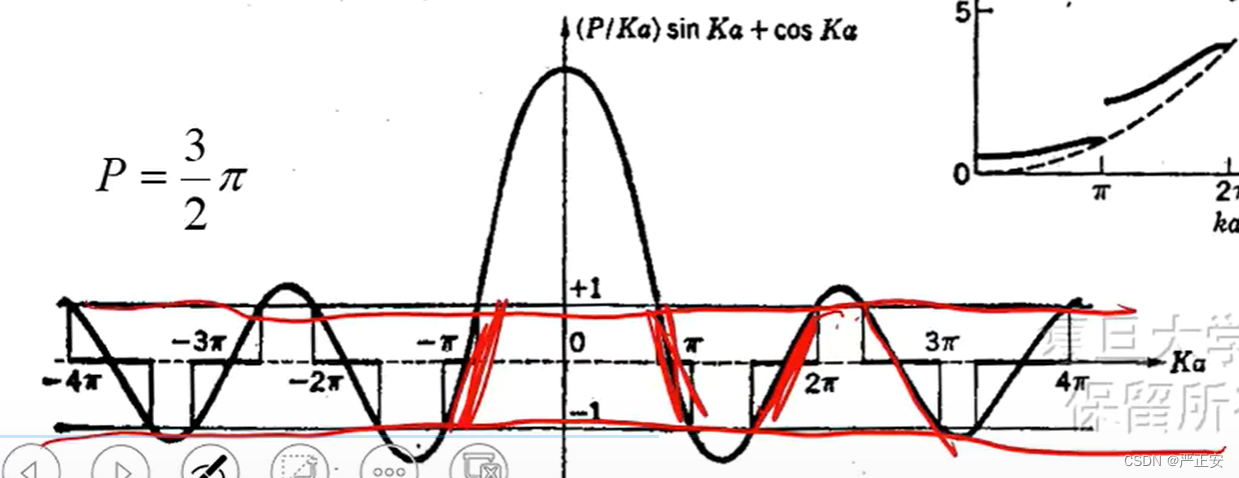
右边的函数的范围,在正负一,约束范围之内的,才是问题的解,对这些交界的地方我们进行分析,大家要时刻记住能量是和K有关系的(我们之前已经解出来了)
,所以我们就看到当
从
变化的时候,也就是
从
变化,从这个曲线交叠上,我们发现,
的横坐标逐渐增加,增加多少,增加一点点,所以平方增加一点点
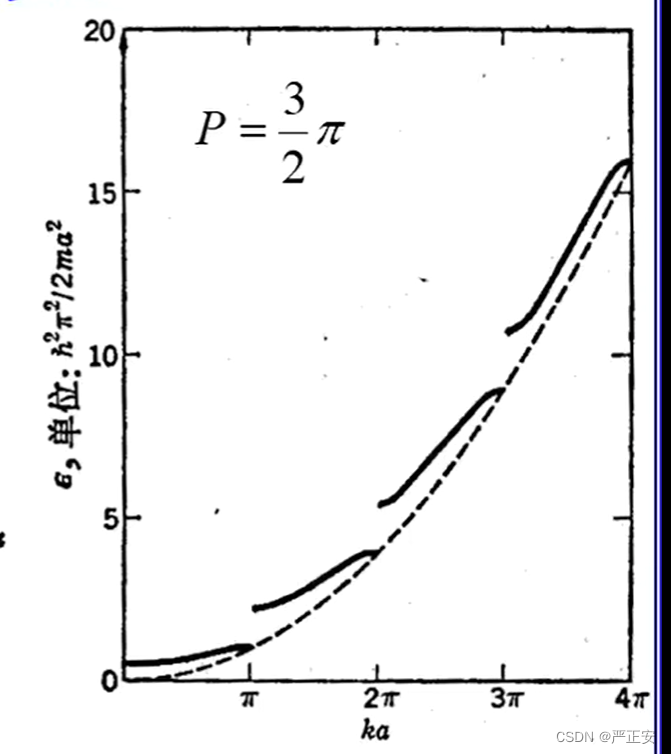
接着下面就是一个非常神奇的现象从
变化的时候,我们既可以向前走,也可以走回头路,我们还是符合上述条件,所以从
并不单单只有一种情况,是一个多值函数
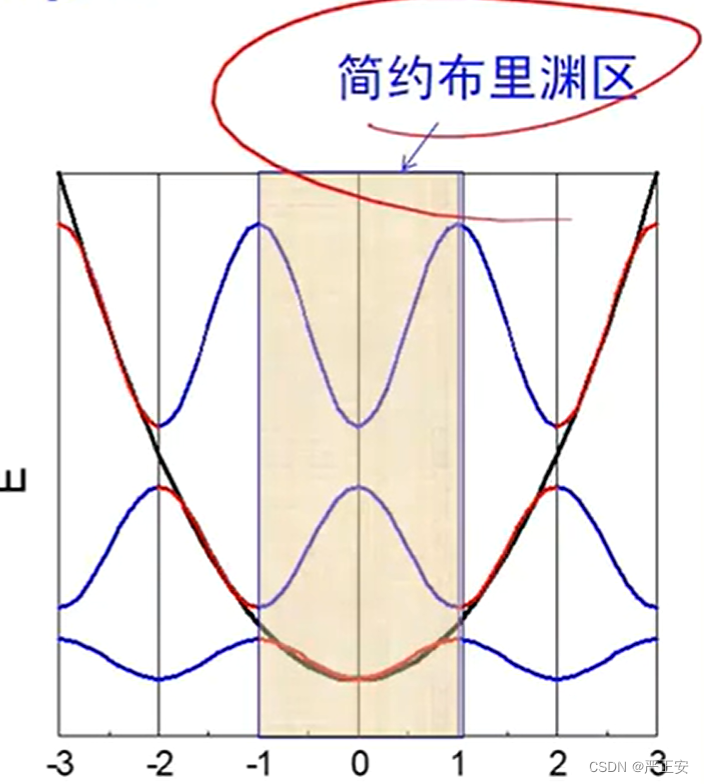
你会发现最终呈现出来的图就会是这个样子,由于周期性的关系,我们只需要关注第一布里渊区,因而我们称之为简约布里渊区
我们总结以下结论
1.能带形成以及能量在倒格子空间中具有周期性
2.所有 关系都可以通过
平移到第一布里渊区,即简约布里渊区
3.同一K值对应多个E,是个多值函数,在阐述关系的时候,要指明适用的具体能带分支