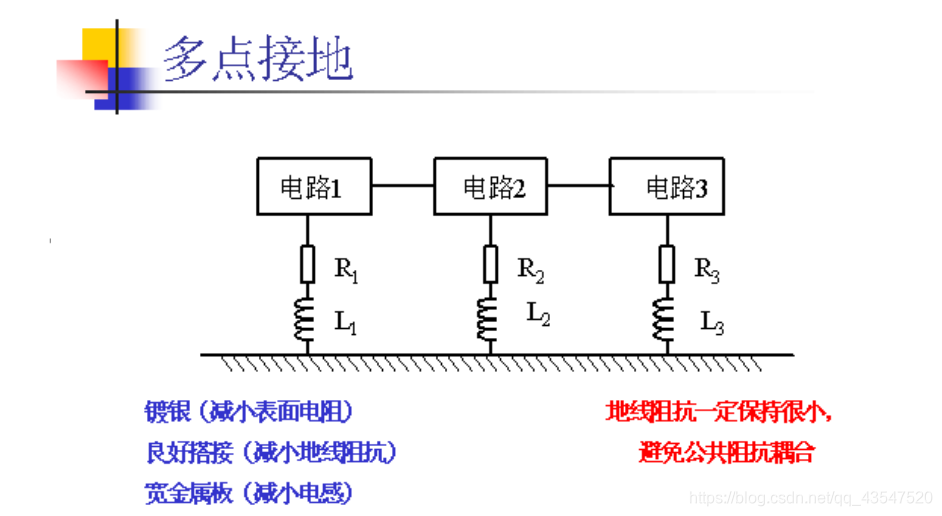
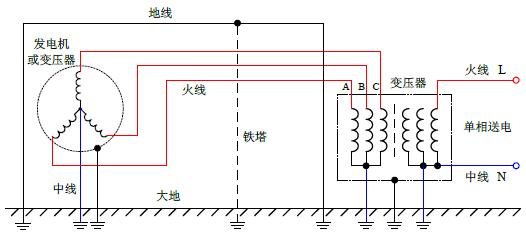
做硬件的应该都学过模电,我也不例外,大学还是作为第一本专业书来学习的,当然这是好多年前的事儿。
模电中分析三极管电路的时候,一般会分析2种情况,直流通路和交流通路。
以下截图就是模拟电路教材的交流通路的分析:
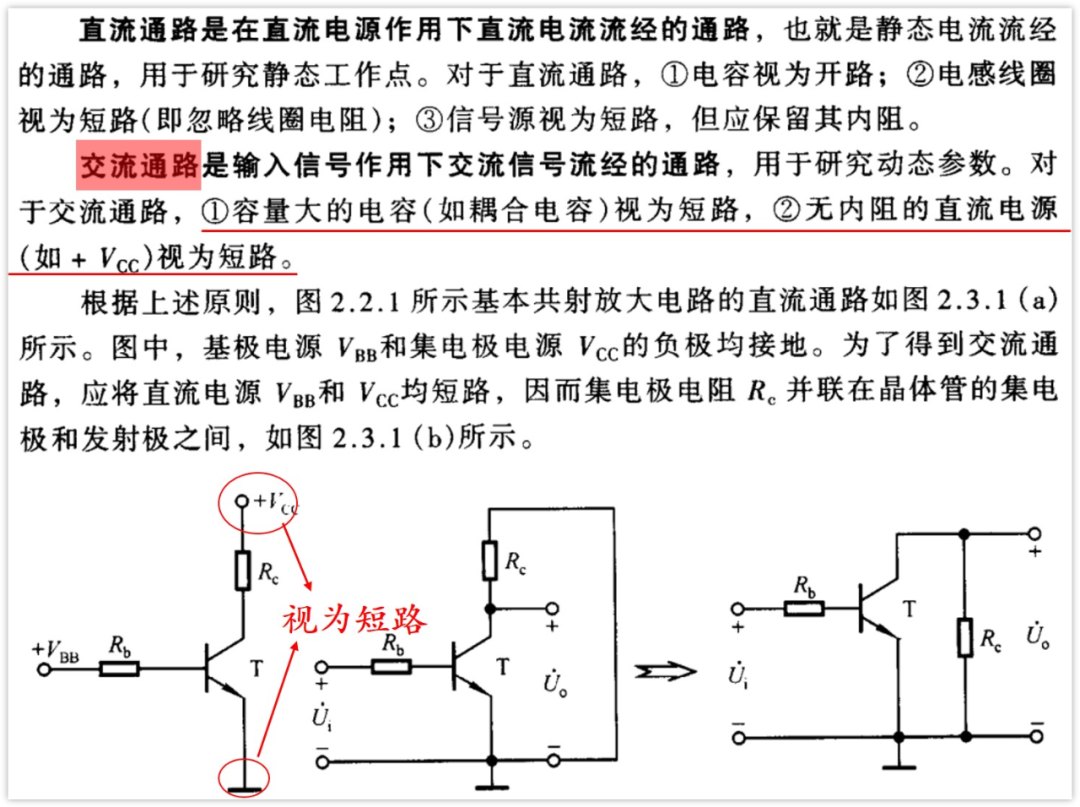
其中有两句话值得看一看:
1、容量大的电容视为短路
2、无内阻的直流电源视为短路
关于这一点,有疑问的人应该不在少数,电容视为短路还好理解一点,电源也视为短路,有点懵。。。
我网上查了一下,比如有下面这样解释:
电源由于其电压恒定不变,即电压变化量等于零,故在交流作用下相当于短路
电源Vcc的内阻很小,相对于交流信号来说,电源Vcc与地GND之间相当于短路
不知道大家觉得这个解释如何,我是看不出来有啥因果关系的。。。。
那如何能通俗理解呢?
关于这一点,我其实想了不少,也查了不少的,最终自己有个想法吧,供参考。
什么是短路?
这还不简单,两点之间用一根导线连接起来,他们之间的阻抗为0,短路最直接的特征就是阻抗为0。

也可以说,如果两个点之间阻抗是0,那么我们也就说它们是短路的。
短路之后最直接的现象就是,短路的两点信号波形一模一样。
感觉像是在说废话。。。。
对于交流信号来说,电容为什么相当于是短路?
交流信号就是指有变化的信号,也就是说有频率,即使看起来杂乱无章的无周期的音频信号,经过傅里叶变换展开,也就是各种频率的正弦波,只是有很多频率分量而已。
电容的阻抗是1/jwC-----(w为角频率=2pi*f,C为电容量)
直流信号的频率可以看成为0Hz,它在分母上,所以电容对直流的阻抗就是无穷大,也就是说电容对直流信号来说相当于开路(开路的特点就是之间阻抗无穷大)。
而对某一频率的交流信号,电容容量越大,阻抗越小。当阻抗小到可以忽略不计的程度,可以看成是0Ω,那也就是相当于短路。
举个例子:
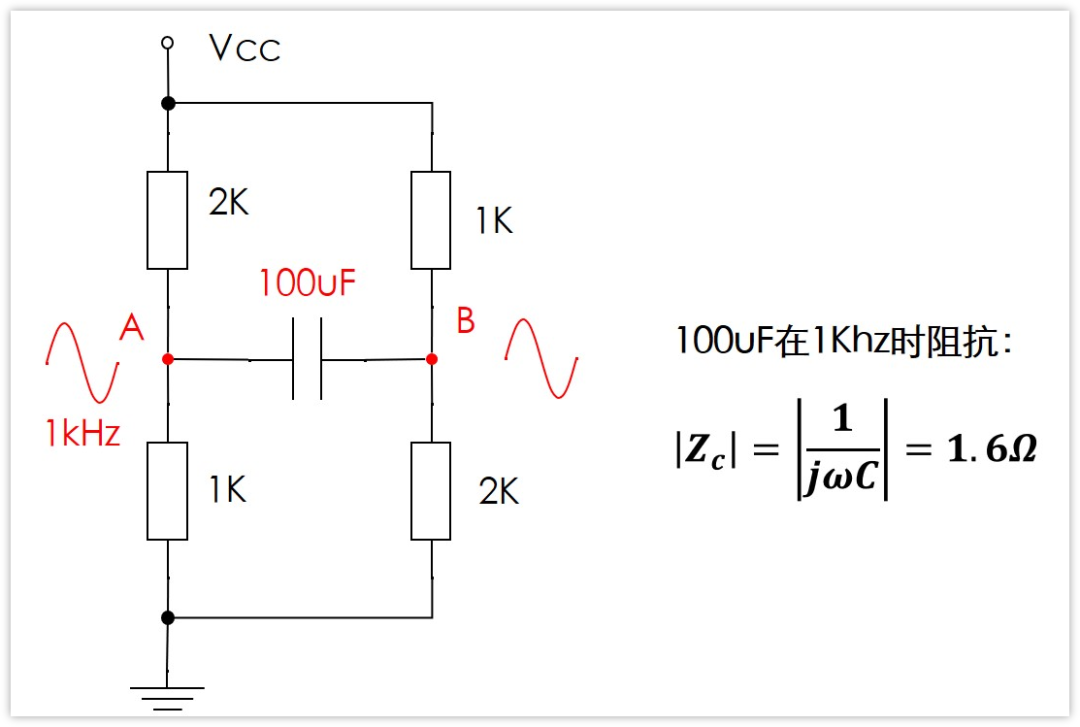
信号的频率是1Khz,电容100uF,那么容抗就是1/jwC=1.6Ω,相对于电路中其它的1K,2K的电阻,这个1.6Ω确实很小。
因此,为了方便分析电路,我们即使把它当作0Ω来看待,也可以得到基本正确的结果(当然,这里对交流信号来说的,直流肯定不行),那么就是说,这个100uF此时是相当于是短路的。
当然了,如果电容容量减小1000倍,是100nF,那么阻抗就是1.6K,显然不能忽略了,也就不能相当于短路了。
这也是为什么教材里面说容量大的电容才能相当于是短路的。
我们可以分别对100uF和100nF的情况做一个简单的仿真,看是不是这样。
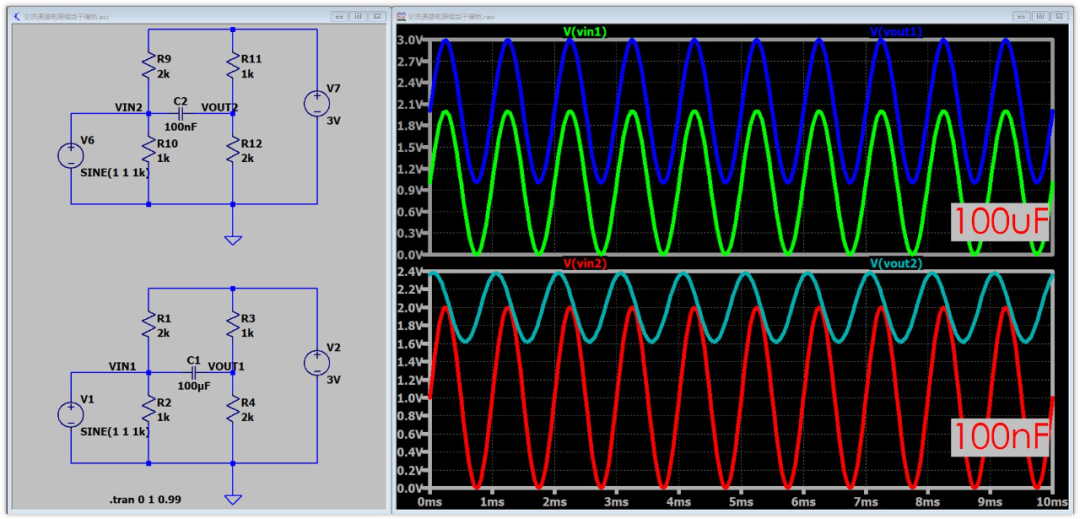
可以看到,在100uF的时候,B点的波形和A点一模一样(不管直流分量)。而在100nF的时候,B点的波形与A点差很多,幅度和相位都不一样。
所以说,只有电容足够大,电容才能看成短路,那具体是多大叫足够大呢?
这个就要看具体电路。我们不能说100uF一定可以看成短路,也不能说100nF一定不可以看成短路。
如果我们考虑的交流信号是1Mhz的,那么100nF电容的阻抗就是1.6Ω,100nF在此时可以看成是短路的。
如果频率是1Khz不变,而上面电路中的电阻都是1MΩ的,那么尽管此时100nF电容的阻抗还是1.6K,但是比起1MΩ电阻来说,还是够小的,我们把它看成短路,也是可以的。
总的来说,电容多大叫够大,要看信号的频率,所处位置其它器件的总的等效阻抗是多大。电容的阻抗如果远小于所处位置的其它器件总的等效阻抗,那么就可以看成是短路的,反之就不可以。
对于交流信号来说,电源为什么相当于是短路?
上面这个电路,如果我们将电容换成直流电源,那么会发生什么呢?
A点输入交流信号,B点一定会获得一个一模一样的交流信号。
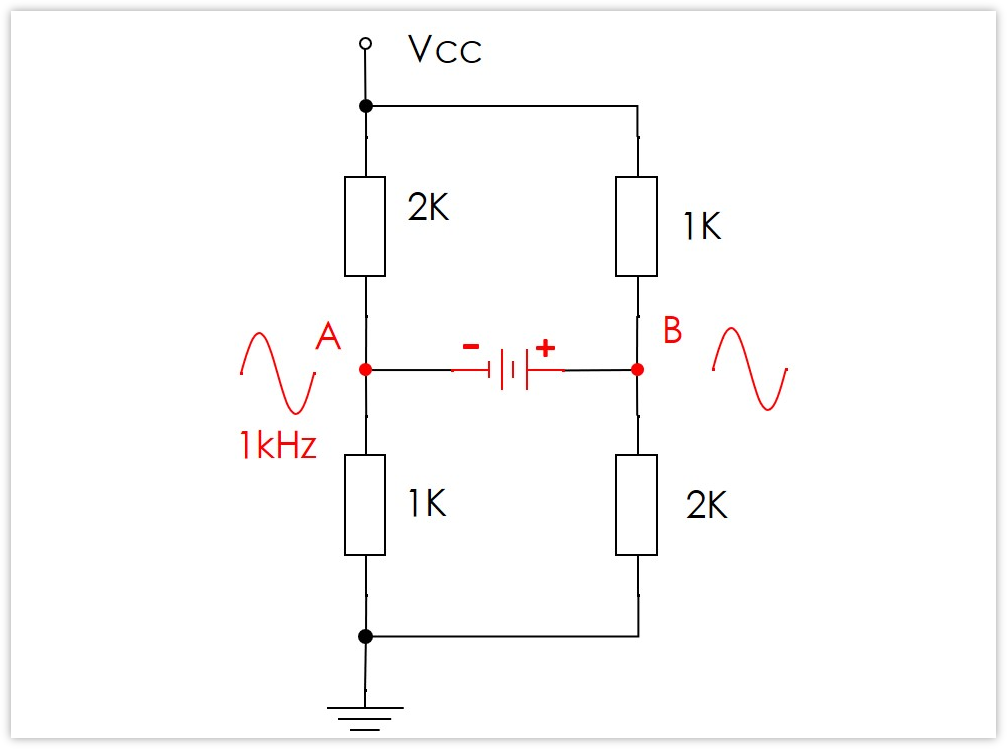
这个很容易理解,假如A点的电压增大△U,因为A和B直接是恒压源电源,两端电压恒定,就是VCC,那么B点的电压一定也增大△U。
这么看,不就是相当于A和B直接接到了一起吗?阻抗为0。
因为它们俩的波形总是一模一样的,没有任何差别。如果阻抗不是0,那么放入到电路中,它们之间的阻抗一定会同电路中其它的器件构成分压,导致波形不一样。
我们也可以看下仿真波形
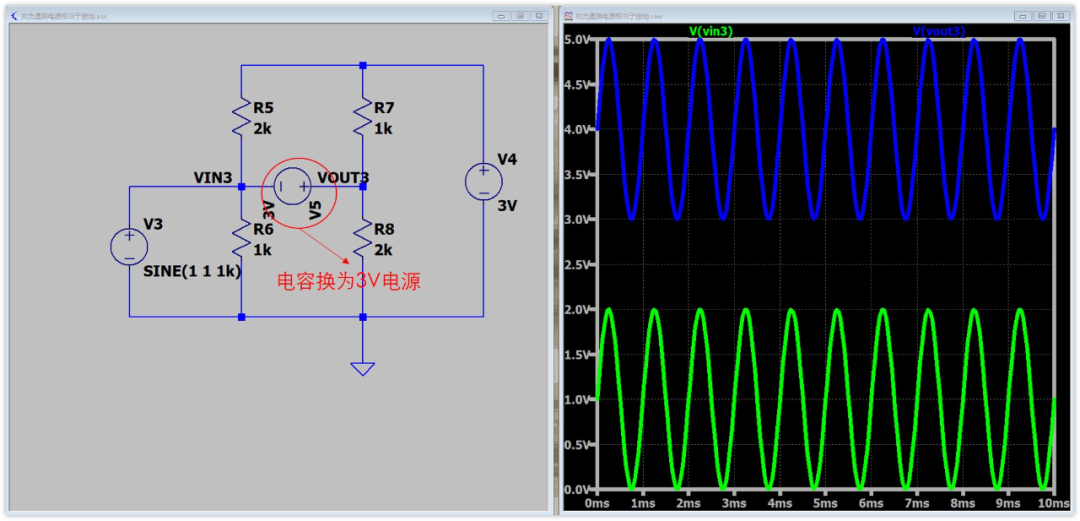
图中加了一个3V的电源,替代之前的电容,可以看到,两点之间的波形也是一模一样的,只是直流电压有个3V的压差。
所以,对于交流信号来说,电源就相当于是短路的,即电源正负极相当于是用一根导线接到一起了,之间交流阻抗为0。
当然严格来说,实际中电源都有内阻r,只是比较小,能忽略掉的话才是相当于是短路的。
另外,标题说“电源相当于接地”,其实不是很准确,只是一般一个电路,电源负极就是地,所以,对于交流信号来说,也就是电源正极VCC相当于接地了。
除此之外,我们应该可以想到,在分析交流信号时,电源相对于电容,是更可以看成短路的。毕竟,电容对信号频率,所处位置的阻抗有要求,而电源基本没啥要求,只要是交流信号,内阻足够小的电源都可以看成是短路的。
以上是纯属个人的理解,如有问题,欢迎在留言区交流。
往期精彩内容:
MOS管电流方向能反吗?体二极管能过多大电流?
NTC热敏电阻与浪涌电流,热启动不会失效?
Buck的振铃实验与分析