比较了采用非线性优化和矩阵乘离散傅里叶变换的三种二维图像配准算法。这些算法的精度与传统的快速算法相当。傅里叶变换上采样方法在一小部分的计算时间和与大大减少内存要求。比较它们的精度和计算时间，以评估平移不变误差度量。

在各种各样的应用中，人们通常希望将两个图像注册到一个像素的一小部分内，以便进行图像处理任务或评估。在这项工作中，我们主要关注通过相位检索来评价重构图像[1,2]，对于这一点，二维刚性平移就足够了。其他应用程序也可以发现,虽然更创收费员转换通常是必需的,在遥感数据的处理,生物和医学图像放大,计算机视觉,与相关任务响ingfrom超限分辨[3],斑纹和噪音增加[4],运动和变更跟踪,和立体视觉[5] [6 - 8]

对于仅在两个图像之间进行转换的情况，解决此问题的常用技术是通过快速傅里叶变换(FFT)计算要注册的图像和参考图像之间的上采样互相关，并定位其峰值。与这种方法相关的计算负担随着注册所需的交流权限的增加而增加，特别是在内存方面。例如，对于1024×1024的图像，在1/20像素范围内进行配准需要20480×20480逆FFT的处理和存储，而目前大多数单点计算机无法做到这一点。

在本文中，我们提出了三种基于非线性优化和离散傅里叶变换(DFTs)的有效的配准算法，它们允许两幅具有较大的采样因子的图像的精确配准。在计算图像质量的平移不变误差度量时，我们测试了这些算法的精度和计算速度。与通常的FFT方法相比，这些算法具有更短的计算时间和更少的内存需求。

对于相位检索重建图像的问题，可以通过测量f(x,y)的傅里叶变换的幅值对f(x,y)的图像g(x,y)进行数值重建[1,2]。在这种情况下，一个重构g(x,y)被认为是成功的，即使它有一个全局坐标平移(x0,y0)或者乘以一个任意常数a。重构的质量必须通过一个对这些操作不变的误差度量来实现。其中一个度量是由[9]定义的f(x,y)和g(x,y)之间的标准化均方根误差(NRMSE) E

$$\begin{array}{rl}{E}^2=& \underset{\alpha ,x_0{y}_0}{\min }\frac{{\sum }_{x,y}{\left|\mathrm{ag}\left(x-x_0,y-y_0\right)-f(x,y)\right|}^2}{{\sum }_{x,y}|f(x,y){|}^2}\\ =& 1-\frac{x_0{y}_0}{{\sum }_{x,y}|f(x,y){|}^2{\sum }_{x,y}|g(x,y){|}^2}\end{array}$$
其中对所有图像点求和(x, y) ;

$$\begin{array}{rl}{r}_{fg}\left(x_0,y_0\right)& =\sum _{x,y}f(x,y)g^{\ast }\left(x-x_0,y-y_0\right)\\ & =\sum _{u,p}F(u,v)G^{\ast }(u,v)\exp \left[i2\pi \left(\frac{u{x}_0}{M}+\frac{v{y}_0}{N}\right)\right]\end{array}$$
为f(x,y)与g(x,y)的互相关;N和M为图像的维数:(*)表示复连词;大写字母表示对应的小写字母的DFT，由关系给出

$$F(u,v)=\sum _{x,y}\frac{f(x,y)}{\sqrt{MN}}\exp \left[-i2\pi \left(\frac{ux}{M}+\frac{vy}{N}\right)\right]$$
E2相对于[9]是最小的。因此，Eq.(1)对NRMSE的评估需要通过定位交叉相关的峰值$r_{fg}(x,y)$来解决更一般的亚像素图像配准问题

通常的FFT方法afraction内找到互相关峰值,$1/\kappa$,一个像素是(i)计算 $F(u,v)$和$G(u,v)$(ii)将$F(u,v)G^{\ast }(u,v)$嵌入尺寸为($\kappa M,\kappa N$)的一组更大的零数组中，(iii)计算逆FFT以获得向上采样的互相关,(iv)定位高峰。在本例中，对于$N⩽M.$，逆FFT的计算复杂度为 O { M N K [ log ⁡ 2 ( κ M ) + κ log ⁡ 2 ( κ N ) ] } O\left\{M N_{K}\left[\log _{2}(\kappa M)+\kappa \log _{2}(\kappa N)\right]\right\} O{MNK​[log2​(κM)+κlog2​(κN)]}。

作为这种方法的有效替代品，我们开发了三种不同的算法，在不牺牲准确性的情况下显著提高了性能。这三种算法都是从FFT方法得到的互相关峰值位置的初始估计开始，向上采样因子${\kappa }_0=2$。这种初始向上采样是用来为可能有不止一个相似磁峰的相互关系选择一个合适的起始点。

第一个算法，首先在[9]中提出，但没有实现，利用非线性优化共轭梯度例程[10]优化初始估计，以最大化${\left|r_{fg}\left(x_0,y_0\right)\right|}^2$。它对$x_0$的偏导数是
∂ ∣ r f g ( x 0 , y 0 ) ∣ 2 ∂ x 0 = 2 Im ⁡ { r f g , y 0 ) ∑ u , v 2 π u M F ∗ ( u , v ) × G ( u , v ) exp ⁡ [ − i 2 π ( u x 0 M + v y 0 N ) ] } \begin{aligned} \frac{\partial\left|r_{f g}\left(x_{0}, y_{0}\right)\right|^{2}}{\partial x_{0}}=& 2 \operatorname{Im}\left\{r_{f g}, y_{0}\right) \sum_{u, v} \frac{2 \pi u}{M} F^{*}(u, v) \\ &\left.\times G(u, v) \exp \left[-i 2 \pi\left(\frac{u x_{0}}{M}+\frac{v y_{0}}{N}\right)\right]\right\} \end{aligned} ∂x0​∂∣rfg​(x0​,y0​)∣2​=​2Im{rfg​,y0​)u,v∑​M2πu​F∗(u,v)×G(u,v)exp[−i2π(Mux0​​+Nvy0​​)]}​
对$y_0$的偏导也有类似的表达式。该算法迭代搜索使$r_{fg}\left(x_0,y_0\right)$最大化的图像位移$\left(x_0,y_0\right)$，并能在任意像素分块内实现配准精度。

第二种算法，我们称之为单步DFT方法，使用了2D DFT的矩阵乘法实现[11.121]。如。(3)、细化初始峰值位置估计。当需要计算上采样互相关的所有点时，二维FFT是最有效的方法。不幸的是，FFT仅限于计算整个上采样阵列的维数$(\kappa M,\kappa N)$，如果我们只对一个非常小的邻域内的$r_{fg}\left(x_0,y_0\right)$的上采样版本的峰值位置的初始估计感兴趣，这将导致巨大的资源浪费。矩阵乘DFT的优势在于，向上采样的$r_{fg}\left(x_0,y_0\right)$可以在这样的邻域内计算，而不需要对$F(u,v)G^{\ast }(u,v)$进行零填充。在单步DFT算法中，初始估计是在一个1.5×1.5像素的邻域内(以原始像素为单位)计算上采样的互相关(由一个因子$\kappa$)。这个运算是由三个维度(1.5$\kappa$,$N$)， ($N$,$M$)和($M$,1.5$\kappa$)的矩阵的乘积来实现的。通过在输出$(1.5\kappa ,1.5\kappa )$数组(以上采样像素为单位)中搜索峰值，实现亚像素配准。假设$\kappa$小于 $M$ and $N$，则上采样的算法复杂度为$O(MN\kappa )$;与FFT上采样法相比有了很大的改进。

随着所需配准精度的提高，在细化初始（$\kappa 0$=2）转换估计值时采用两步矩阵乘DFT方法证明进一步减少计算样本的数量很有用。两步DFT算法最初对1.5×1.5像素区域进行升采样，采样率约为初始估计的${\kappa }_1\simeq {\kappa }^{1/2}$，并在该阵列中找到互相关峰值。在第二步中，通过对新估计周围的原始像素网格的$3/{\kappa }_1\times 3/{\kappa }_1$较小区域进行上采样全因数来进一步细化峰位置。以这种方式，细化算法的复杂度降低到$O\left(MN{\kappa }^{\mathrm{i}/2}\right)$。对于FFT，单步和两步DFT方法，这种平移估计的精度(${\kappa }^{-1}$)与FFT相同

为了评估和比较各种算法的性能，我们使用相加的零均值圆形com形高斯噪声$n(x,y)$对一个256×256复值图像$f(x,y)$进行了破坏，并通过$\left(x_0,y_0\right)$ =(502/21,52/15)像素对其进行了平移以生成$g(x,y)$。本例中不变NRMSE E的估计结果如图1(a)所示，相对于真实的NRMSE E，其中$E^2={\sum }_{x,y}|n(x,y){|}^2/{\sum }_{x,y}|f(x,y){|}^2$。当NRMSE趋近于0时，使用高赋值因子k或非线性优化例程变得至关重要，以避免对e的过高估计。通过计算移位误差($\Delta r=[{\left(x_0-{\hat{x}}_0\right)}^2{+\left(y_0-{\hat{y}}_0\right)]}^{1/2}$如图1(b) for $E$=0.25所示)来确定估计平移量(xo,jo)的精度。为了便于比较，我们还将得到的Ar与不需要指定k的非线性优化例程进行了比较。对于$E$=0.25这一较大的值，使用较高的上采样因子(即$K$=10)进行估计，得到的收益递减[图3]。1(a)]，但是从图1(b)中可以看出，更大的k值和更大的非线性优化算法对配准精度有显著的好处。最终配准精度将受到噪声的限制。

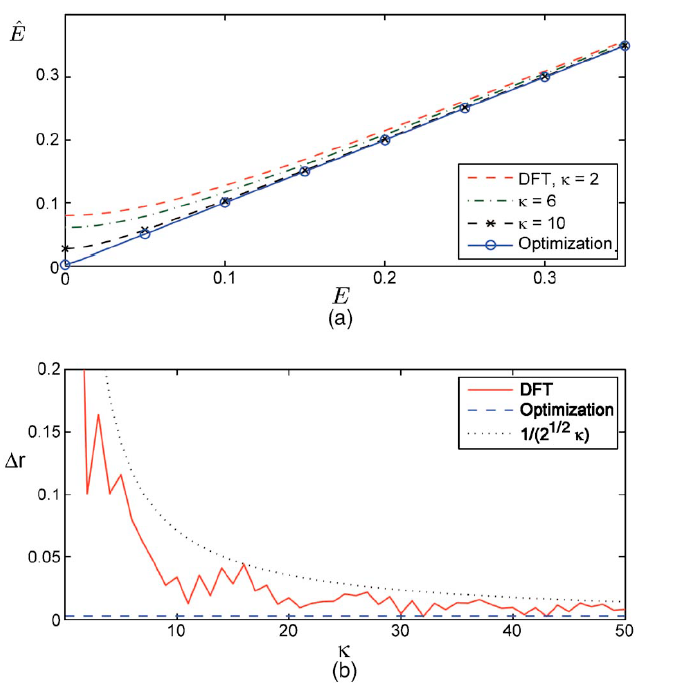
图1所示。(a)不变的NRMSE估计值与E (b) E=0.25时估计图像位移Ar与上采样因子k的误差。虚线表示无噪声的最大误差1/(\2k)。对于优化算法，Ar=0.0029像素(虚线曲线)。

三种算法在台式机(AMD Athlon X2双核处理器2.21 GHz, 64位操作系统，4 Gbytes RAIM)上的计算时间比较如图2所示。2×上采样FFT方法获得ini估计所需的时间包含在时间测量中，并明确显示以供比较。初步估计被发现支配了总计算时间。图2(a)显示了$E$=0.22时配准算法相对于图像大小的计算时间(DFT算法的$\kappa$=25)。对于相同噪声量的512×512张图像，计算时间k的函数如图2(b)所示。给出了非线性优化算法的计算时间，并进行了比较;它与$\kappa$无关。假设两个双精度复值数组，在同一台计算机上可以执行FFT的最大阵列大小为11585×11585。这相当于传统FFT上采样方法的最大图像大小为463×463,$\kappa$=25，取235 s，而单步DFT算法取0.78 s。注意，使用FFT upsampling方法注册$\kappa$=25的2048 x 2048个图像需要超过78 gb的RAM。

与单步DFT方法相比，两步DFT方法在计算时间上减少的上采样量与图像大小有关。相交点分别出现在图像大小为64×64、256×256和512 x 512的$\kappa$= 20,30和45处。虽然非线性优化方法在任何情况下都是最耗时的，但由于它不受向上采样因子的限制，并且可以检索任意的分数阶变换值，因此具有最高的精度。

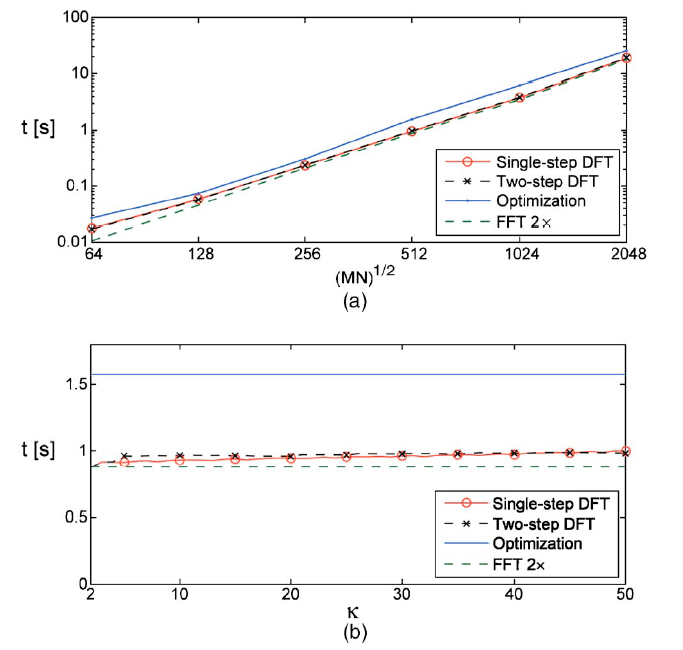
图2所示。(彩色在线)相对于(a)图像大小(DFT算法为$\kappa =25$)和(b) 512 x 512图像的上采样因子的计算时间。

通过互相关实现的亚像素图像配准特别适合于相位检索重建的图像的比较，在相位检索中，将翻译后的解乘以一个全局复杂因子被认为是一种成功的配准。在低噪声环境下，利用非线性优化或高阶采样因子对E的精确计算尤为重要。翻译估计的准确性很大程度上得益于较大的上采样因子，即使存在中等数量的噪声。这三种算法可以直接扩展到包含互相关方法的变量，如相位相关，并包含窗口函数来计算边缘效果[13]。

虽然其他方法(如曲线拟合互相关峰值[4]或随机抽样方法[81])可以显著更快地实现亚像素图像配准，但它们在配准过程中牺牲了精度。与FFT上采样方法一样，我们的算法总是使用图像中所有可用的信息来计算初始估计和上采样互相关网格中的每个点，从而使它们对噪声具有很强的鲁棒性。

线性优化算法)，但大大减少了计算时间和内存需求。使用这些算法可以精确地注册大型图像，甚至在需要的情况下可以精确到百分之一像素内，在普通的桌面计算机上可进行计算管理，对于任何需要亚像素图像注册的应用程序来说，这将被证明是一个巨大的优势。

部分工作以[14]的形式呈现。

Efficient subpixel image registration algorithms

References

1. J. R. Fienup, Opt. Lett. 3, 27 (1978).
2. J. R. Fienup, Appl. Opt. 21, 2758 (1982).
3. M. Irani and S. Peleg, CVGIP: Graph. Models Image Process. 53, 231 (1991).
4. A. R. Wade and F. W. Fitzke, Opt. Express 3, 190(1998).
5. M. D. Pritt, J. Opt. Soc. Am. A 10, 2187 (1993).
6. L. G. Brown, ACM Comput. Surv. 24, 325 (1992).
7. B. Zitová and J. Flusser, Image Vis. Comput. 21, 977 (2003).
8. P. Viola and W. M. Wells III, Int. J. Comput. Vis. 24, 137 (1997).
9. J. R. Fienup, Appl. Opt. 36, 8352 (1997).
10. W. H. Press, S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery, Numerical Recipes in Fortran 77 (Cambridge U. Press, 1992).
11. H. H. Barrett and K. J. Myers, Foundations of Image Science (Wiley, 2004), p. 172.
12. R. Soummer, L. Pueyo, A. Sivaramakrishnan, and R. J. Vanderbei, Opt. Express 15, 15935 (2007).
13. S. T. Thurman and J. R. Fienup, Proc. SPIE 6233,62330S (2006).
14. M. Guizar-Sicairos, S. T. Thurman, and J. R. Fienup, in Signal Recovery and Synthesis, 2007 OSA Technical Digest Series (Optical Society of America, 2007), SMC3.