题目详情：

02-线性结构1 两个有序链表序列的合并

本题要求实现一个函数，将两个链表表示的递增整数序列合并为一个非递减的整数序列。

函数接口定义：

List Merge( List L1, List L2 );

其中List结构定义如下：

typedef struct Node *PtrToNode;
struct Node {ElementType Data; /* 存储结点数据 */PtrToNode   Next; /* 指向下一个结点的指针 */
};
typedef PtrToNode List; /* 定义单链表类型 */

裁判测试程序样例：

#include <stdio.h>
#include <stdlib.h>typedef int ElementType;
typedef struct Node *PtrToNode;
struct Node {ElementType Data;PtrToNode   Next;
};
typedef PtrToNode List;List Read(); /* 细节在此不表 */
void Print( List L ); /* 细节在此不表；空链表将输出NULL */List Merge( List L1, List L2 );int main()
{List L1, L2, L;L1 = Read();L2 = Read();L = Merge(L1, L2);Print(L);Print(L1);Print(L2);return 0;
}/* 你的代码将被嵌在这里 */

输入样例：

输出样例：

1 2 3 4 5 6 8 10 
NULL
NULL

主要思路：

创建一个新链表的虚拟头结点，三个指针依次指向新链表,L1,L2，逐项比较L1和L2节点并将其接入新链表，最后如果L1和L2长度不等则把剩余的一次性接入新链表

第一次写错误：

（1）题目表述“L1和L2是给定的带头结点的单链表”，意思是L1与L2最初传进来的是虚拟头结点

（2）注意本题最后要求的输出L1与L2均为NULL，所以是可以直接操作L1和L2指针，如果不操作，则两者最后下一位都要指向NULL

（3）题目表述“返回归并后的带头结点的链表头指针”，意思是最后返回的链表要带虚拟头结点

（4）本题构建非递减链表，所以应该是L1与L2中小的加入新链表

代码实现：

List Merge( List L1, List L2 ) {List dummyHead = (List)malloc(sizeof(struct Node));dummyHead -> Next = NULL;List cur1 = L1 -> Next;List cur2 = L2 -> Next;List cur3 = dummyHead;while(cur1 && cur2) {if(cur1 -> Data <= cur2 -> Data) {cur3 -> Next = cur1;cur1 = cur1 -> Next;cur3 = cur3 -> Next;cur3 -> Next = NULL;}else {cur3 -> Next = cur2;cur2 = cur2 -> Next;cur3 = cur3 -> Next;cur3 -> Next = NULL;}}if(cur1) cur3 -> Next = cur1;else cur3 -> Next = cur2;L1 -> Next = NULL;L2 -> Next = NULL;return dummyHead;
}

题目详情：

02-线性结构2 一元多项式的乘法与加法运算

设计函数分别求两个一元多项式的乘积与和。

输入格式:

输入分2行，每行分别先给出多项式非零项的个数，再以指数递降方式输入一个多项式非零项系数和指数（绝对值均为不超过1000的整数）。数字间以空格分隔。

输出格式:

输出分2行，分别以指数递降方式输出乘积多项式以及和多项式非零项的系数和指数。数字间以空格分隔，但结尾不能有多余空格。零多项式应输出0 0。

输入样例:

4 3 4 -5 2  6 1  -2 0
3 5 20  -7 4  3 1

输出样例:

15 24 -25 22 30 21 -10 20 -21 8 35 6 -33 5 14 4 -15 3 18 2 -6 1
5 20 -4 4 -5 2 9 1 -2 0

主要思路：

求和的其实课本上讲过了，就是分别遍历L1和L2，

（1）两者如果指数不等则将指数大的节点加入新链表，同时移动新链表与加入节点的指针;

（2）两者如果指数相等则系数相加，同时要判断两者是否为0，不为0时再把合并后接入新链表

（3）如果最后L1或L2有多余直接一次性接入

本题难点在于乘法

我的思路是利用之前实现的多项式加法函数，将多项式乘法转化为多项式加法

（1）用L1的每一项乘整个L2，得到一个多项式

（2）将新得到的多项式与L1前一项与整个L2相乘结果相加

如此便可以得到最终乘法结果

第一次写错误：

（1）尾插法不熟悉

void attach(int coef, int expo, ptrnode* rear) {	//这个函数是用来向函数尾结点插入节点，传入的形参ptrnode* rear是二级指针，是指向原链表尾结点指针的地址 ptrnode newnode = (ptrnode)malloc(sizeof(node));newnode -> coef = coef;newnode -> expo = expo;newnode -> next = NULL;(*rear) -> next = newnode;	//多定义一个尾指针能提高往尾部插入的效率 (*rear) = newnode;
}

如果定义dummyHead -> next = NULL, 然后rear = dummyHead -> next, 那么rear就一直是空指针！不会在dummyHead后面接节点

（2）在没有特殊说明的情况下，传入的链表都默认是不含虚拟头结点的

代码实现：

#include <stdio.h>
#include <malloc.h>
struct node {	//定义节点int coef;int expo;struct node* next;
};
typedef struct node node;
typedef node* ptrnode;	//这个表示指向每个节点的指针 
typedef ptrnode list;	//这个表示链表 
list createDummyHead(list L) {	//日常操作链表大都需要向头部加一个虚拟头节点 ptrnode dummyHead = (ptrnode)malloc(sizeof(node));dummyHead -> next = L;return dummyHead;
}
int compare(int e1, int e2) {	//比较两个多项式指数 int ret = 0;if(e1 > e2) ret = 1;else if(e1 < e2) ret = -1;else ret = 0;return ret;
}
void deleteList(list L) {	//这个函数用来删除整个链表 ptrnode dummyHead = (ptrnode)malloc(sizeof(node));dummyHead -> next = L;ptrnode cur = dummyHead -> next;while(cur) {ptrnode tmp = cur;cur = cur -> next;free(tmp);}free(dummyHead);return;
} 
void attach(int coef, int expo, ptrnode* rear) {	//这个函数是用来向函数尾结点插入节点，传入的形参ptrnode* rear是二级指针，是指向原链表尾结点指针的地址 ptrnode newnode = (ptrnode)malloc(sizeof(node));newnode -> coef = coef;newnode -> expo = expo;newnode -> next = NULL;(*rear) -> next = newnode;	//多定义一个尾指针能提高往尾部插入的效率 (*rear) = newnode;
}
list readPolynomial() {	 //这个函数是用来读取链表 ptrnode rear, dummyHead, tmp;dummyHead = (ptrnode)malloc(sizeof(node));dummyHead -> next = NULL;rear = dummyHead;int nodeNum = 0;scanf("%d", &nodeNum);while(nodeNum--) {int coef, expo;scanf("%d %d", &coef, &expo);attach(coef, expo, &rear);}tmp = dummyHead;ptrnode head = dummyHead -> next;free(tmp);return head;
}
void printList(list L) {if(L == NULL) {printf("0 0");return;}ptrnode tmp = L;while(tmp) {printf("%d %d", tmp -> coef, tmp -> expo);if(tmp -> next) printf(" ");tmp = tmp -> next;}return;
}
list polySum(list L1, list L2) {ptrnode cur1 = L1;ptrnode cur2 = L2;ptrnode dummyHead, rear;dummyHead = (ptrnode)malloc(sizeof(node));dummyHead -> next = NULL;rear = dummyHead;	 while(cur1 && cur2) {int firstExpo = cur1 -> expo;int secondExpo = cur2 -> expo;int integrateCoef = 0;switch(compare(firstExpo, secondExpo)) {case 1:attach(cur1 -> coef, cur1 -> expo, &rear);cur1 = cur1 -> next;break;case -1:attach(cur2 -> coef, cur2 -> expo, &rear);cur2 = cur2 -> next;break;case 0:	//尤其要注意同类型合并 integrateCoef = cur1 -> coef + cur2 -> coef;if(integrateCoef) attach(integrateCoef, cur1 -> expo, &rear);cur1 = cur1 -> next;cur2 = cur2 -> next;break;}}while(cur1) {	 //这是处理有一个多项式还有剩余，就把它剩余项一起接到结果多项式后面 attach(cur1 -> coef, cur1 -> expo, &rear);cur1 = cur1 -> next;}while(cur2) {attach(cur2 -> coef, cur2 -> expo, &rear);cur2 = cur2 -> next;}ptrnode tmp = dummyHead;ptrnode ans = dummyHead -> next;free(dummyHead);return ans;
}
list polyProduct(list L1, list L2) {ptrnode cur1 = L1;ptrnode cur2 = L2;ptrnode ansDummyHead = (ptrnode)malloc(sizeof(node));ansDummyHead -> next = NULL;	while(cur1) {	//用L1的每一项与L2整个相乘，L1的不同项就会对应不同的链表，然后把这些链表两两相加，可以调用之前写的求和函数 ptrnode tmpDummyHead = (ptrnode)malloc(sizeof(node));tmpDummyHead -> next = NULL;ptrnode tmpRear = tmpDummyHead;while(cur2) {attach(cur1 -> coef * cur2 -> coef, cur1 -> expo + cur2 -> expo, &tmpRear);cur2 = cur2 -> next;}list tmp = tmpDummyHead -> next;	//这里要注意tmp摆放位置，如果在定义空节点后就定义tmp是空节点下一位，那么tmp就一直是NULL！！！ list formerList = ansDummyHead -> next;ansDummyHead -> next = polySum(tmp, formerList);deleteList(formerList);deleteList(tmp);free(tmpDummyHead);cur1 = cur1 -> next;cur2 = L2;}	list answer = ansDummyHead -> next;free(ansDummyHead);return answer;
}
int main(void) {list L1 = readPolynomial();list L2 = readPolynomial();
//	printList(L1);
//	putchar('\n');list product =  polyProduct(L1, L2);list sum = polySum(L1, L2);printList(product);putchar('\n');printList(sum);deleteList(L1);deleteList(L2);return 0;
}

题目详情：

02-线性结构3 Reversing Linked List

分数 25

全屏浏览题目

切换布局

作者陈越

单位浙江大学

Given a constant K and a singly linked list L, you are supposed to reverse the links of every K elements on L. For example, given L being 1→2→3→4→5→6, if K=3, then you must output 3→2→1→6→5→4; if K=4, you must output 4→3→2→1→5→6.

Input Specification:

Each input file contains one test case. For each case, the first line contains the address of the first node, a positive N (≤105) which is the total number of nodes, and a positive K (≤N) which is the length of the sublist to be reversed. The address of a node is a 5-digit nonnegative integer, and NULL is represented by -1.

Then N lines follow, each describes a node in the format:

Address Data Next

where Address is the position of the node, Data is an integer, and Next is the position of the next node.

Output Specification:

For each case, output the resulting ordered linked list. Each node occupies a line, and is printed in the same format as in the input.

Sample Input:

00100 6 4
00000 4 99999
00100 1 12309
68237 6 -1
33218 3 00000
99999 5 68237
12309 2 33218

Sample Output:

00000 4 33218
33218 3 12309
12309 2 00100
00100 1 99999
99999 5 68237
68237 6 -1

代码长度限制

16 KB

时间限制

400 ms

内存限制

64 MB

简单翻译：

本题就是输入了一个乱序的链表，只是告诉你每个节点的地址，数据域与下一个节点的地址，要先顺出一个完整链表，然后还要倒置指定长度，如果剩下长度不足指定长度就不倒置

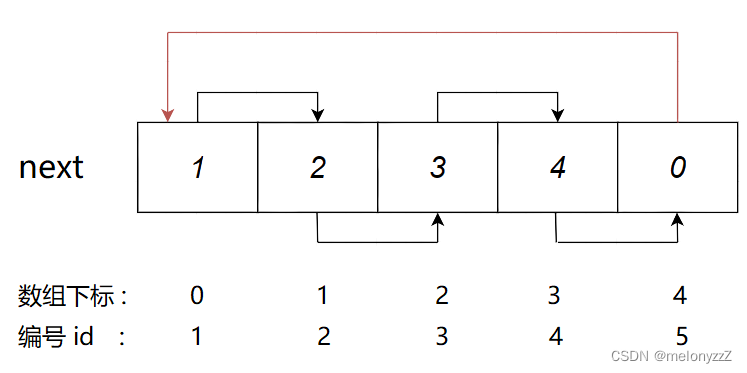
主要思路：

用两个大数组，一个存储每个节点的地址数组1，另一个存储每个节点的详细信息数组2，这样在倒置链表时只要用双指针法操作存储每个节点的地址的数组1，然后遍历数组1，利用数组1存储的当前节点地址访问存储每个节点的详细信息的数组2，打印其详细信息即可

第一次写错误：

肝了两天多，没想出来，什么纯链表，纯大数组，链表加大数组……

代码实现：

#include <stdio.h>
#include <stdlib.h>
#define maxsize 100002struct LNode {int Data;int Next;
} a[maxsize];	//a这个数组是用来存储数据 int list[maxsize];  //每个结点的地址
int Head, N, K, p;  //第一个节点地址,所有结点数,翻转子序列长度int main() {scanf("%d%d%d", &Head, &N, &K);list[0] = Head;for (int i = 0; i < N; ++i) {int index, data, next;scanf("%d%d%d", &index, &data, &next);a[index].Data = data;a[index].Next = next;}p = a[Head].Next;int sum = 1;while (p != -1) {list[sum++] = p;p = a[p].Next;}int j = 0;while (j + K <= sum) {	//双指针法 int left = j, right = j + K - 1;while (left < right) {int temp = list[left];	//操作的是记录地址的指针 list[left] = list[right];list[right] = temp;left++;right--;}j = j + K;}for (int i = 0; i < sum - 1; ++i) {int id = list[i];  //第i个结点的索引printf("%05d %d %05d\n", id, a[id].Data, list[i + 1]);	//直接打印交换后的下一个地址，原来记录在a里的下一位没用了 }printf("%05d %d -1\n", list[sum - 1], a[list[sum - 1]].Data);return 0;
}
/*这种思路桥面在用两个大数组，一个用来记录当前节点的数据域与下一个指针，另一个数组用来记录当前节点的地址
双指针法交换节点的时候其实交换当前节点的地址即可*/

题目详情：

02-线性结构4 Pop Sequence

分数 25

全屏浏览题目

切换布局

作者陈越

单位浙江大学

Given a stack which can keep M numbers at most. Push N numbers in the order of 1, 2, 3, ..., N and pop randomly. You are supposed to tell if a given sequence of numbers is a possible pop sequence of the stack. For example, if M is 5 and N is 7, we can obtain 1, 2, 3, 4, 5, 6, 7 from the stack, but not 3, 2, 1, 7, 5, 6, 4.

Input Specification:

Each input file contains one test case. For each case, the first line contains 3 numbers (all no more than 1000): M (the maximum capacity of the stack), N (the length of push sequence), and K (the number of pop sequences to be checked). Then K lines follow, each contains a pop sequence of N numbers. All the numbers in a line are separated by a space.

Output Specification:

For each pop sequence, print in one line "YES" if it is indeed a possible pop sequence of the stack, or "NO" if not.

Sample Input:

5 7 5
1 2 3 4 5 6 7
3 2 1 7 5 6 4
7 6 5 4 3 2 1
5 6 4 3 7 2 1
1 7 6 5 4 3 2

Sample Output:

YES
NO
NO
YES
NO

代码长度限制

16 KB

时间限制

400 ms

内存限制

64 MB

简单翻译：

本题就是告诉你一个最大空间为m的堆栈，往这个堆栈里面依次加入1~n的数字，再给n个测试顺序，判断每个顺序能否实现

主要思路：

（1）利用一个v数组存储每次的测试顺序，cur指针指向第一个

（2）先将1~n数字依次加入堆栈

（3）如果栈顶数字与cur所指向数字不同，继续向堆栈里加入数字；如果相同那就弹出栈顶数字，同时将cur后移一位，直到cur与栈顶数字不同

（4）如果堆栈已满数字还没加完，说明此情况不行

（5）如果数字已加完，flag为true且堆栈为空，说明可以

第一次写错误：

说实话，我一开始都没思路，参考完人家方法虽然看懂了但还不太理解为什么这么想

代码实现：

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>#define MAX_SIZE 1005typedef struct {int data[MAX_SIZE];	//存储元素的数组，可以考虑用指针实现 int top;
} Stack;				//定义了一个Stack类型 void init(Stack *s) {s->top = -1;
}bool push(Stack *s, int x, int m) {		//入栈操作，x是要压入栈头的元素，m是栈的大小 if (s->top == m - 1) return false;	//因为是数组实现，所以要先判断栈有没有满，准备再用链表实现 s->data[++(s->top)] = x;return true;
}int pop(Stack *s) {	//删除并返回栈顶元素 if (s->top == -1) return false;		//先判断堆栈是否为空 return (s->data[(s->top)--]);
}int main() {int m, n, k;scanf("%d%d%d", &m, &n, &k);for (int i = 0; i < k; i++) {Stack s;	//	Stack是类型名称，s才是具体变量 init(&s);int v[MAX_SIZE];for (int j = 0; j < n; j++)scanf("%d", &v[j]);int cur = 0;bool flag = true;for (int j = 1; j <= n; j++) {if (!push(&s, j, m)) {flag = false;break;}while (s.top != -1 && s.data[s.top] == v[cur]) {int x = pop(&s);cur++;}}if (flag && s.top == -1)printf("YES\n");elseprintf("NO\n");}return 0;
}