浅谈拉格朗日插值法
好像FFT要用到,所以就学习一手
文章目录
- 浅谈拉格朗日插值法
- 什么是插值
- 拉格朗日插值法
什么是插值
在离散数据的基础上补插连续的函数,使得这条连续函数经过所有离散数据点,这个过程就叫插值。
其意义在于:
插值是离散函数逼近的重要方法,利用它可通过函数在有限个点处的取值状况,估算出函数在其他点处的近似值。
理解一下:
就是把一个足球踢出去,假设球始终在一个平面上飞行,它的轨迹就可以抽象为 f ( x ) f(x) f(x) (假设这个函数至于时间有关)
现在你有一些照片,所以你可以得到某几个时间点球的位置,想要还原出这个函数 f ( x ) f(x) f(x) 的轨迹。但是你的照片数量是有限的,而函数的点是连续的所以插值的结果 g ( x ) g(x) g(x) 可能有无穷多种
插值有许多方法,包括:三角函数插值;线性插值法;牛顿插值法;拉格朗日插值法 …… 但是蒟蒻只会拉格朗日插值法
拉格朗日插值法
这个方法很简单,相当于硬性拼凑。
举个例子,现在平面上有三个点分别是 ( x 1 , y 1 ) , ( x 2 , y 2 ) , ( x 3 , y 3 ) ( x 1 < x 2 < x 3 ) (x_1 , y_1),(x_2 , y_2),(x_3 , y_3)(x_1 < x_2 < x_3) (x1,y1),(x2,y2),(x3,y3)(x1<x2<x3),我们用这三个插值。
我们需要构造 n n n (这里是3)个函数。第 i i i 个函数满足:
{ 0 , x = x j ( j ! = i ) 1 , x = x i o t h e r s , I d o n ′ t c a r e \left\{\begin{matrix} 0 , x = x_j (j != i) \\ 1 , x = x_i \\ others , I \ don't \ care \end{matrix}\right. ⎩ ⎨ ⎧0,x=xj(j!=i)1,x=xiothers,I don′t care
这是第一个:
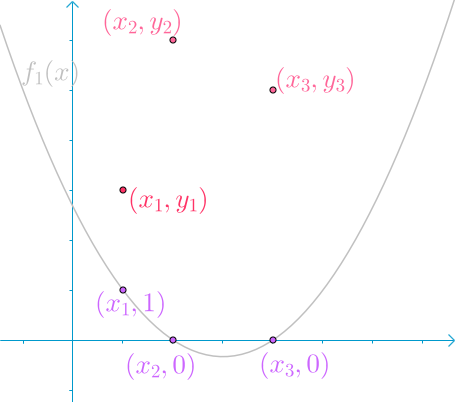
第二个:
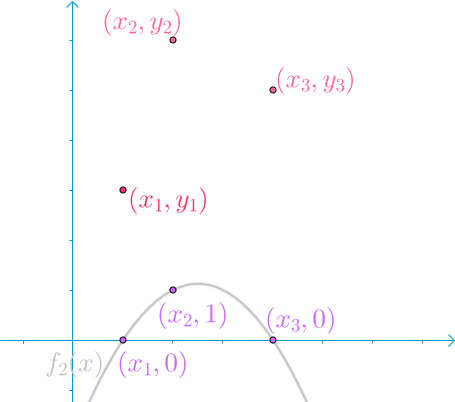
第三个
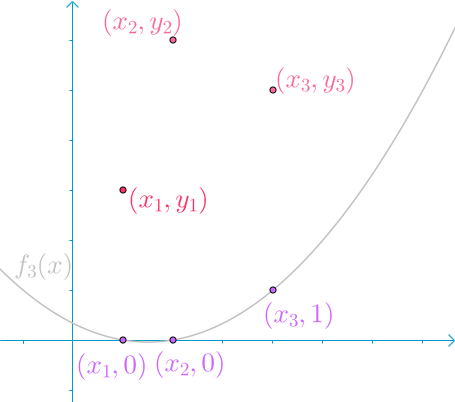
然后我们发现 f ( x ) = y 1 f 1 ( x ) + y 2 f 2 ( x ) + ⋯ + y n f n ( x ) f(x) = y_1f_1(x) + y_2f_2(x) + \cdots + y_nf_n(x) f(x)=y1f1(x)+y2f2(x)+⋯+ynfn(x)
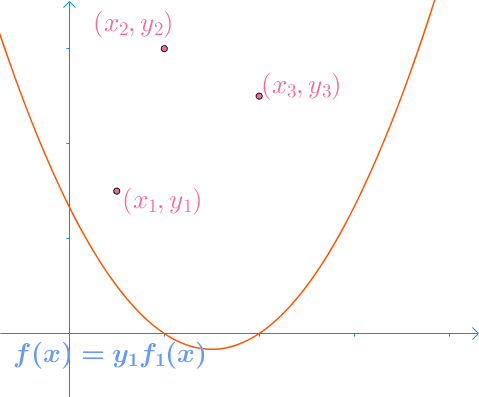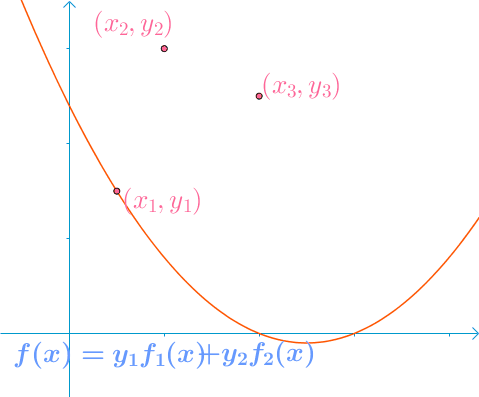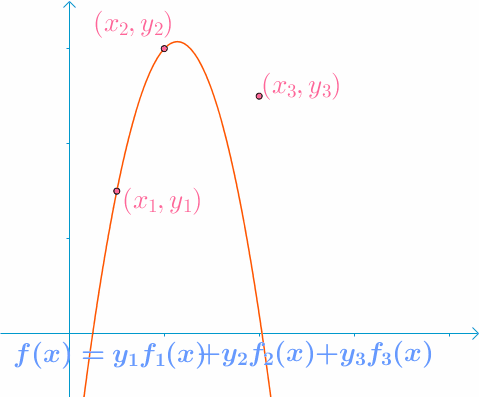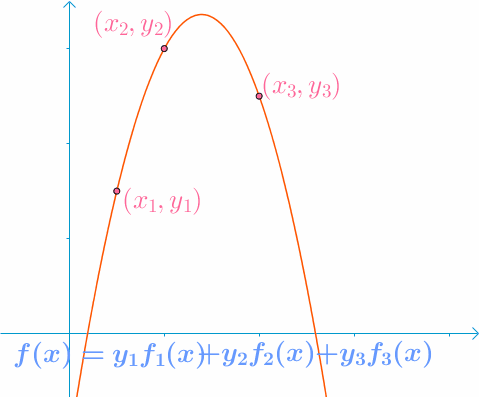
对于我们构造出来的第一 1 1 1 条曲线显然满足性质:
f 1 = ( x − x 2 ) ( x − x 3 ) ( x 1 − x 2 ) ( x 1 − x 3 ) f_1 = \dfrac{(x - x_2)(x - x_3)}{(x_1 - x_2)(x_1 - x_3)} f1=(x1−x2)(x1−x3)(x−x2)(x−x3)
进一步推广:
f i ( x ) = ∏ j ≠ i n x − x j x i − x j f_i(x) = \prod_{j \neq i} ^ {n}\dfrac{x - x^j}{x_i - x_j} fi(x)=j=i∏nxi−xjx−xj
然后就有了:
f ( x ) = ∑ i = 1 n y i ∗ f i ( x ) f(x) = \sum_{i = 1}^{n}y_i*f_i(x) f(x)=i=1∑nyi∗fi(x)
##code
#include <bits/stdc++.h>
#define fu(x , y , z) for(int x = y ; x <= z ; x ++)
#define LL long long
using namespace std;
const LL mod = 998244353;
LL n , k;
struct RE {LL x , y;
}re[2005];
LL read () {LL val = 0 , fu = 1;char ch = getchar ();while (ch < '0' || ch > '9') {if (ch == '-') fu = -1;ch = getchar ();}while (ch >= '0' && ch <= '9') {val = val * 10 + (ch - '0');ch = getchar ();}return val * fu;
}
LL ksm (LL x , LL y) {LL ans = 1;while(y) {if(y&1) ans = ans * x %mod;x = x * x % mod;y >>= 1;}return ans;
}
int main () {LL ans = 0 , ans1;n = read () , k = read ();fu (i , 1 , n) {re[i].x = read () , re[i].y = read ();}fu (i , 1 , n) {ans1 = re[i].y;fu (j , 1 , n)if (i ^ j)ans1 = 1ll * (ans1 * (k - re[j].x) % mod) * ksm (re[i].x - re[j].x , mod - 2) % mod;ans = (ans + ans1+mod) % mod;}printf ("%lld" , ans);return 0;
}