第三题
2508. 添加边使所有节点度数都为偶数
- 连接一条边,一定会让两个点的奇偶性改变。最多连接两条边,最多有四个点的奇偶性改变。所以超过了四个点为奇数点,就不可能了。
并且,由于一次改变两个,奇数点的个数一定是偶数。那么奇数点的个数只能是0, 2, 4。所以可以直接分类讨论:
-
如果是0, 直接返回true
-
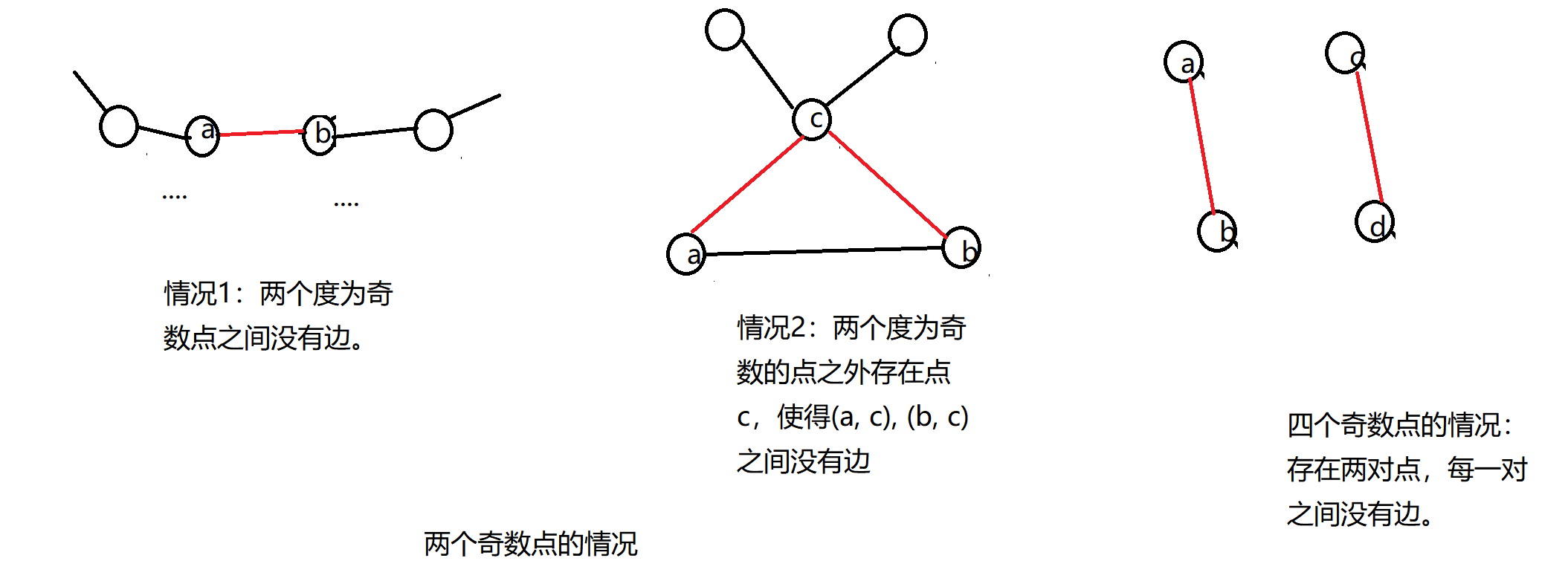
如果是2, 有两种情况正确:
- 两个奇数点,a和b,他们之间没有边,可以直接相连。
- 他们之外存在一个点c,这个点和a和b都没有边。
-
如果是4,只有一种情况:他们之间可以形成两对点,每对点的两个点不相连。
实现方面,因为要多次检查两个点之间是否有边,所以可以写一个函数进行判断。
class Solution {
public:static const int maxn = 1e5 + 5;vector<int>g[maxn];bool check(int a, int b) {// unordered_map<int, int>aset;for (int v : g[a]) {if (v == b) return false;}return true;}bool isPossible(int n, vector<vector<int>>& edges) {unordered_map<int, int>d;for (auto vec : edges) {int a = vec[0], b = vec[1];g[a].push_back(b);g[b].push_back(a);d[a]++;d[b]++;}vector<int>p;for (auto [a, b] : d) {if (b % 2 == 1) p.push_back(a);}if (p.size() > 4 || p.size() % 2 != 0) return false;if (p.size() == 0) return true;if (p.size() == 2) {int a = p[0], b = p[1], flag = 1;if (check(a, b)) return true;for (int i = 1; i <= n; i++) if (check(a, i) && check(b, i)) return true;return false;}// p.size() == 4;if (check(p[0], p[1]) && check(p[2], p[3])) return true;if (check(p[0], p[2]) && check(p[1], p[3])) return true;if (check(p[0], p[3]) && check(p[1], p[2])) return true;return false;}
};
第四题
很明显就是最近公共祖先,并且完全二叉树的性质。
p[a] = a / 2;
超时代码:
- 先找到a的所有父结点,存入map,
- 遍历b的父结点,找到a,b的最近公共祖先
- 再次遍历,计算a到祖先和b到祖先的最近距离之和。
- 答案等于结果加上1。
时间复杂度O(m * n * n)
class Solution {
public:vector<int> cycleLengthQueries(int n, vector<vector<int>>& queries) {vector<int>ans;for (auto vec : queries) {int a = vec[0], b = vec[1];unordered_map<int, int>fa;int p = a;fa[p] = 1;while (p != 1) {p /= 2;fa[p] = 1;}p = b;while (true) { // 找到公共的爹, 就是pif (fa[p]) break;p /= 2;}int cnt = 0;while (a != p) a /= 2, cnt++;while (b != p) b /= 2, cnt++;ans.push_back(cnt + 1);}return ans;}
};
不超时的代码
时间复杂度O(n * m)
class Solution {
public:vector<int> cycleLengthQueries(int n, vector<vector<int>>& queries) {vector<int>ans;for (auto vec : queries) {int a = vec[0], b = vec[1];int cnt = 1;while (a != b) {cnt++;if (a < b) swap(a, b);a >>= 1;}ans.push_back(cnt);}return ans;}
};