LeetCode——Weekly Contest 321

这段时间经历了组会、开题、回家等等，这才发现周赛已经打到325场了，而我还没有写完321场的题解记录，真是汗颜啊。

LeetCode周赛第321场记录

这场周赛的题目相对比较简单一些，在此简单做个梳理：

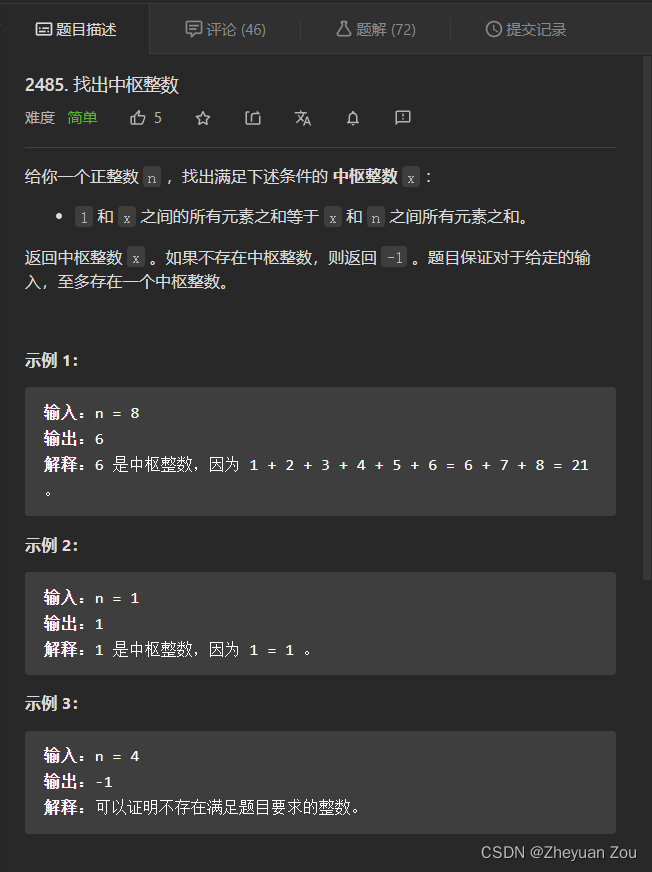
在这里插入图片描述
这道题比较简单，就是找出[1,n]之间的一个"中枢"值。

这道题我使用了等差数列的求和公式来快速计算一个范围内的和，随后通过一次遍历来实现中枢值的查找，代码如下：


class Solution {/* complexity:O(1) */int getSum(int Start, int End)		// 左闭右闭区间{int Length = End - Start + 1;return (int)((Start + End) * ((double)Length / 2));}
public:int pivotInteger(int n) {int Ans = -1;/* Compexity: O(n) */for(int i = 1 ; i <= n ; ++i)if(getSum(1, i) == getSum(i, n)){Ans = i;break;}return Ans;}
};

、
注意在上述代码计算范围和时，除以2的部分一定要转成double类型，否则0.5会被整除抹去导致结果出错。

2486. 追加字符以获得子序列(贪心)

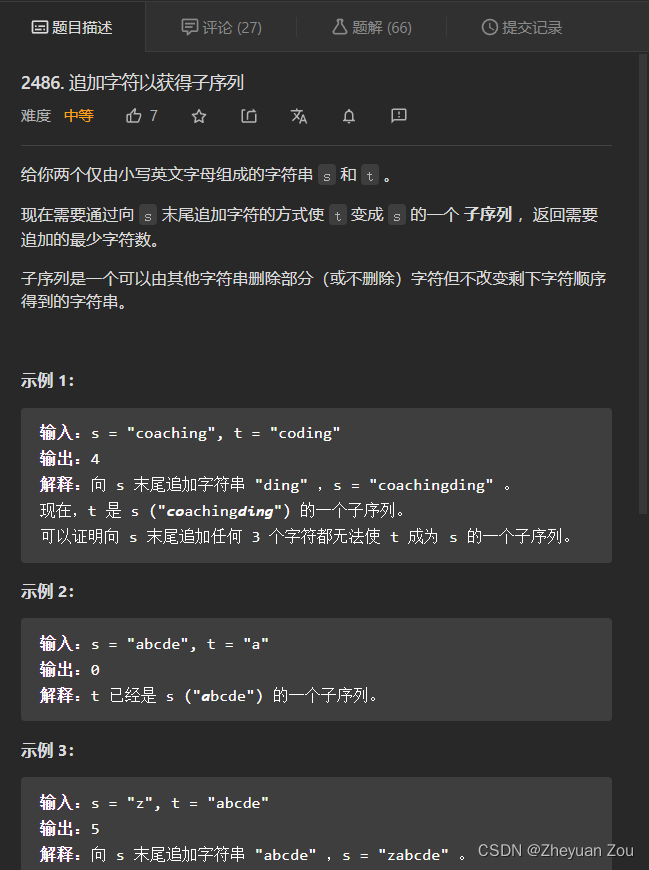
在这里插入图片描述
这道题也同样非常简单，因为子序列是不连续的，所以只需要贪心地统计字符串s中已经出现了的t的子序列长度即可，再用t的长度减去已经匹配的长度即可，代码如下：

class Solution {
public:int appendCharacters(string s, string t) {int n = s.size(), m = t.size();int i = 0, j = 0;	// i,j分别指向要匹配的下一个字符while(i < n and j < m){while(i < n and s[i] != t[j])++i;		// 如果没有匹配到，那么持续递增iif(i == n)		// 如果已经到了S的结尾，那么直接跳出循环break;else			// 否则说明匹配到了相同字符，i、j均向后移动{++i;++j;}}return m - j;		// 最终看j指针停留在哪里，这就是缺少的字符数量}
};

2487. 从链表中移除节点(单调递增栈)

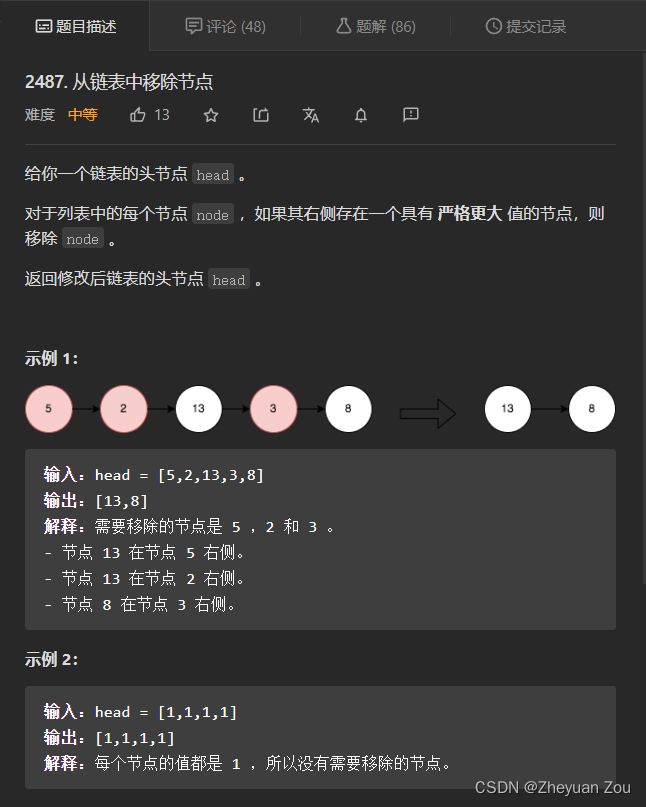
在这里插入图片描述
这道题一种比较好的解法就是单调栈，在使用单调栈时可以先将一个很大的Dummy节点推到栈中，这个节点是始终不会被推出栈的，这可以帮助我们快速索引到栈底元素从而返回答案。

随后开始遍历链表，并同时使用单调栈维护一个单调不增的序列，这样就可以在 $O (n)$ 的时间复杂度内完成本题的求解，代码也非常简洁优雅，所以这道题中Dummy节点的使用是非常漂亮的，很好地利用了题目中链表节点取值范围的信息。

ListNode* removeNodes(ListNode* head) {ListNode* ans = new ListNode(1e6);stack<ListNode*> st;st.push(ans);while(head) {while(head->val > st.top()->val) st.pop();st.top()->next = head;st.push(head);head = head->next;}return ans->next;        }

2488. 统计中位数为 K 的子数组(数学转换)——O(n)

在这里插入图片描述
这道题是一道考察转化的问题，这里记录一下灵茶山艾府的笔记。
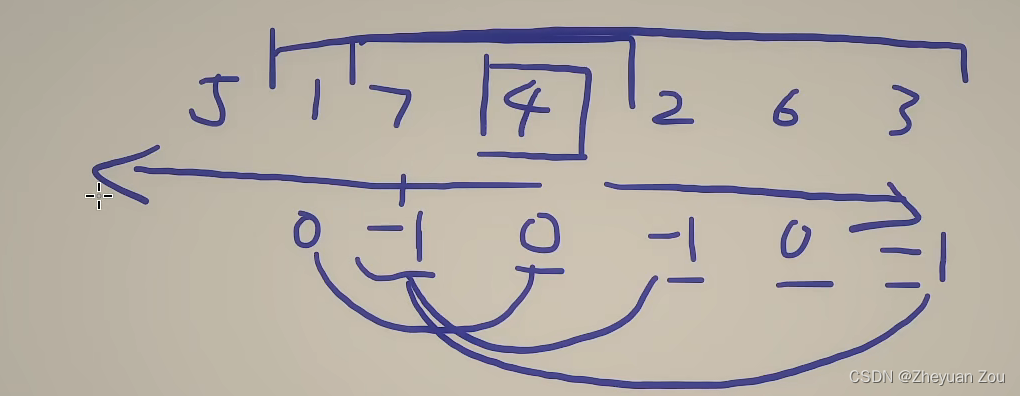
注意这道题对于中位数的定义，当子数组长度为偶数时，直接取中间两个元素的靠左的元素，而不是平均数，这和数学上的中位数定义是不一样的。

// 问题转化思路，首先明确子数组意味着连续，那么我们不能对原先数组进行排序，因为这样会打乱数组元素顺序// CaseI：如果是奇数长度的数组，那么存在一个数k是中位数意味着小于k和大于k的数字一样多
// 左侧小于k的数字个数 + 右侧小于k的数字个数 = 左侧大于k的数字个数 + 右侧大于k的数字个数
// 移项得到：左侧小于k的数字个数 - 左侧大于k的数字个数 = 右侧大于k的数字个数 - 右侧小于k的数字个数// 将上式中正项看作+1：那么右侧大于k的数字可以看作+1，左侧小于k的数字可以看作+1
// 负项看作-1：那么右侧小于k的数字可以看作-1，左侧大于k的数字可以看作-1
// 按照这样的做法从k向两侧统计，左侧累计计数值 = 右侧累计计数值即可//CaseII：如果使偶数长度的数组，因为我们要找的是靠左的中位数，那么上式改为：
// 左侧小于 - 左侧大于 + 1 = 右侧大于 - 右侧小于
// 具体在实施时，只需要保证左侧累计计数值 + 1 = 右侧累计计数值
// 完整代码如下：
int countSubarrays(vector<int> &nums, int k) {/*首先找到k的索引位置，这个位置一定是唯一的*/int pos = find(nums.begin(), nums.end(), k) - nums.begin(), n = nums.size();unordered_map<int, int> cnt;cnt[0] = 1;     // 这是因为[k]自身组成的数组一定满足中位数是k/*1.从k开始向右统计，大于k加一，小于k减一，并不断更新计数值*/for (int i = pos + 1, c = 0; i < n; ++i) {c += nums[i] > k ? 1 : -1;++cnt[c];}/*2.从k开始向左统计，大于k减一，小于k加一，并不断将符合要求的值累加入答案*/int ans = cnt[0] + cnt[1]; for (int i = pos - 1, c = 0; i >= 0; --i) {c += nums[i] < k ? 1 : -1;ans += cnt[c] + cnt[c + 1];     // cnt[c]对应长度为奇数的情况，cnt[c+1]对应长度为偶数的情况}return ans;}