汉诺塔的非递归算法

对于汉诺塔问题，我们都普遍认为这个是一个典型的递归问题，然而递归需要使用到系统对应的栈，开销比较大，因此我在想使用非递归算法来解决它，然而网上绝大部分的教程都是自己模拟了一个栈，因此我在考虑写一篇blog记录一下。

问题描述

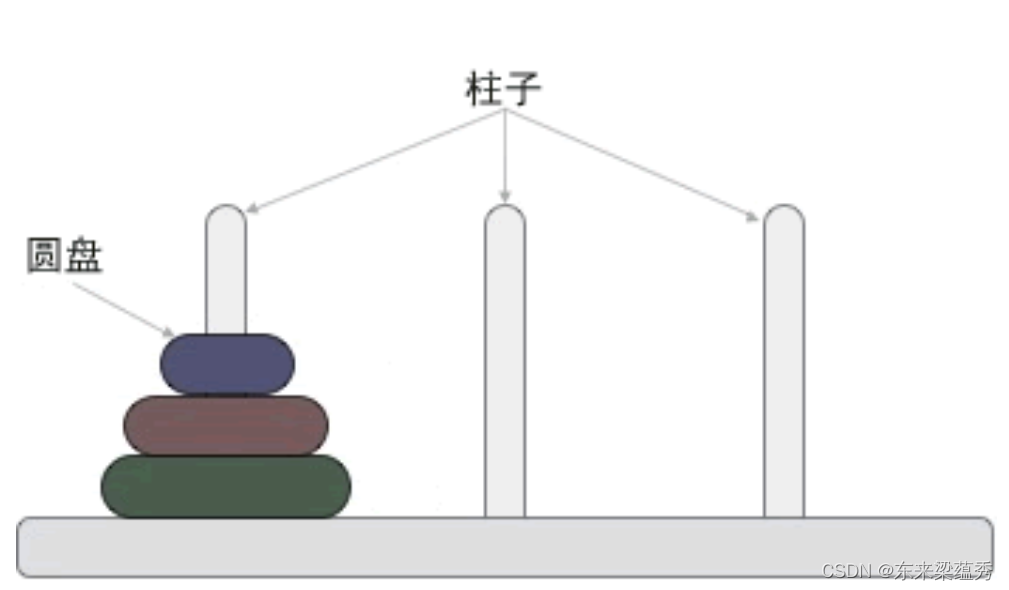
将一个柱子中的所有圆盘移动到另一个柱子，移动过程需遵守以下规则：每次只能移动一个圆盘，而且只能移动某个柱子上最顶部的圆盘；移动过程中，必须保证每个柱子上的大圆盘都位于小圆盘的下面。
在这里插入图片描述

递归算法

这个算法还算比较好理解，我们计A，B，C盘,那么假设我们要把n圆盘，从A移到C，可以拆分为小问题,我们把上面n-1个的圆盘看成整体,让它先到B，那么最下面的一个移动到C，再把n-1个从B移动到C。
这样就把复杂问题，拆分成更简单的问题，那么退出条件就是只剩下一个圆盘，即为，A->C

#include<iostream>
using namespace std;
//算法设计实验1，汉诺塔问题
//采用递归方法解决
//n个棋盘  A B C为基座   最终达成目标A全部移到C
//性能 T(n)=2T(n-1)+1  1忽略 那么时间复杂度为O(2^n)，相当的大，因此对于n较大的时候，运行时间较长
void Hanoi1(int n,char A,char B,char C)
{if (n == 1){cout  << A << " -> "<< C << endl;return;}Hanoi1(n - 1, A, C, B);//相当于先把上面n-1盘子，移到中间cout<< A << " -> " << C << endl;Hanoi1(n - 1, B, A, C);//相当于先把上面n-1盘子，移到中间
}
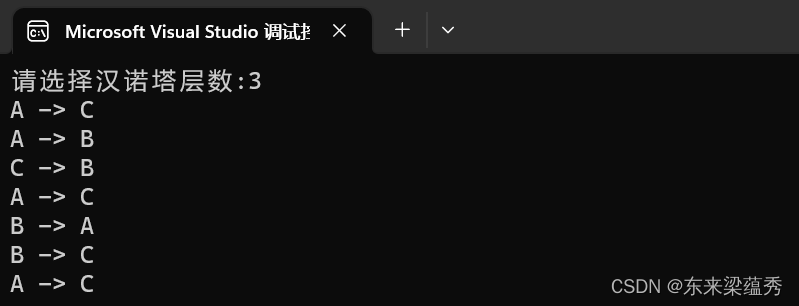
int main()
{int n;cout << "请选择汉诺塔层数:";cin >> n;//递归算法Hanoi1(n, 'A', 'B', 'C');return 0;
}

非递归运行结果

非递归算法

当然我参考的时候发现，很多人模拟了栈作为非递归算法，这种当然可以，但是其核心思想还是用栈的方法，实现递归，本质上和系统的栈思想一致。因此我在考虑用真正非递归的思想来解决这个问题。
由于问题较为复杂，因此咱们先举出比较简单的例子。
假设只有2个盘子
在这里插入图片描述

步骤	1	2	3	4	5	6	7
移动的盘子	0	1	0	2	0	1	0
步骤	0->2	0->1	2->1	0->2	1->0	1->2	0->2

我们可以发现其中是有规律的：

如果把三个柱子围成一个环，盘子总数为N，
如果N为偶数：奇数号盘每次2步；偶数号盘每次1步；
如果N为奇数：奇数号盘每次1步；偶数号盘每次2步；
当三个柱子都不为空则优先移动最小的盘子。

#define N 150
#define X dish[i].dnum
#define Y dish[i].lnum
#define SP dish[i].peg
//向右走一步
struct dish
{int dnum;	//自身编号int lnum;	//下面的盘子int peg;	//所在的柱子
}dish[N];
//初始化每个柱的状态为空
int s[3] = {};
//向右走一步
int mov1(int sp, int x)
{if (s[(sp + 1) % 3] > x)//要移动的目标是可以承载当前盘子的{//printf("\nmove1\n");printf("%d %d --> %d\n", x, sp, (sp + 1) % 3);s[dish[x].peg] = dish[x].lnum; //x盘所在柱子减去当前盘，顶盘变为x盘的下一个dish[x].lnum = s[(dish[x].peg + 1) % 3]; //x盘的落点即x转移后的下面的盘s[(dish[x].peg + 1) % 3] = dish[x].dnum; //x盘转移到的柱子顶盘值变为x盘值dish[x].peg = (dish[x].peg + 1) % 3; //x盘所在柱子变为落点柱子return 1; //转移成功}else return 0; //转移失败
}
//向右走两步
int mov2(int sp, int x)
{if (s[(sp + 2) % 3] > x)//要移动的目标是可以承载当前盘子的{//printf("\nmove2\n");printf("%d %d --> %d\n", x, sp, (sp + 2) % 3);s[dish[x].peg] = dish[x].lnum; //x盘所在柱子减去当前盘，顶盘变为x盘的下一个dish[x].lnum = s[(dish[x].peg + 2) % 3]; //x盘的落点即x转移后的下面的盘s[(dish[x].peg + 2) % 3] = dish[x].dnum; //x盘转移到的柱子顶盘值变为x盘值dish[x].peg = (dish[x].peg + 2) % 3; //x盘所在柱子变为落点柱子return 1; //转移成功}else return 0; //转移失败
}
int main()
{int n;cout << "请选择汉诺塔层数:";cin >> n;int i, change = 1, j;for (i = 0; i < n; i++){dish[i].dnum = i; //作为盘子的唯一标识,顶层为0,最高级的最大盘子为N-1dish[i].lnum = i + 1; //底层盘子的下一层为N，即空柱dish[i].peg = 0; //初始化，所有盘子都在A柱	}s[0] = 0; //当前0柱上最顶端的盘子值s[1] = n;s[2] = n;//空柱，屏蔽大于n的盘子while (s[0] < n || s[1] < n){j = 0;for (i = 0; s[j] <= n && i < n; i++) //不为空柱则向下找盘子{if (s[0] >= n && s[1] >= n)return;if (s[dish[i].peg] != dish[i].dnum) //当上面有盘子时不能移动continue;if ((n % 2 == 0 && X % 2 == 0) || (n % 2 == 1 && X % 2 == 1))change = mov1(SP, X);else change = mov2(SP, X);if (!change){if (s[0] < n && s[1] < n && s[2] < n){for (int k = 0; s[k] != 0; k++)j = k;}else j = (j + 1) % 3; //该柱上没有盘子可以移动则更换柱子}}}return 0;
}