怎么判断数字n是否为2的x次方，即2的幂次呢？比如2,4,8,16,32

提示：一些位运算的技巧

---

文章目录

• 怎么判断数字n是否为2的x次方，即2的幂次呢？比如2,4,8,16,32
• • @[TOC](文章目录)
• 题目
• 如果n & (n-1) = 0，n就是2的幂次
• 总结

题目

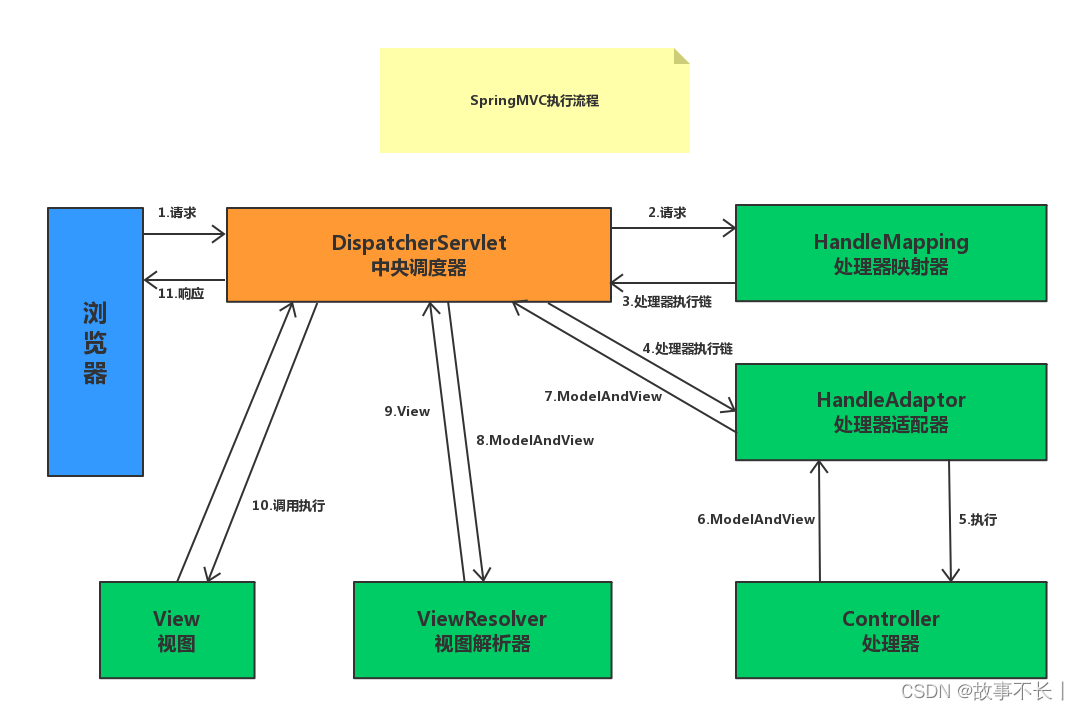
怎么判断数字n是否为2的x次方，即2的幂次呢？比如2,4,8,16,32

---

如果n & (n-1) = 0，n就是2的幂次

看计算机中存的二进制数
2=10
4=100
8=1000
……

因此，2的幂次方，说白了就是二进制数里面有一个1，但是1不在0位上
那我们对n取反是啥感觉？
n中1变0,0变1

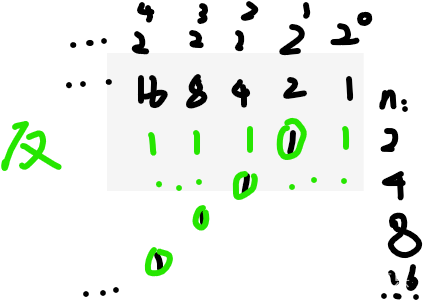
显然n & (!n)=0对吧，没问题的

那我且问你，n是2的幂次这种二进制数，n-1是多少呢？
比如

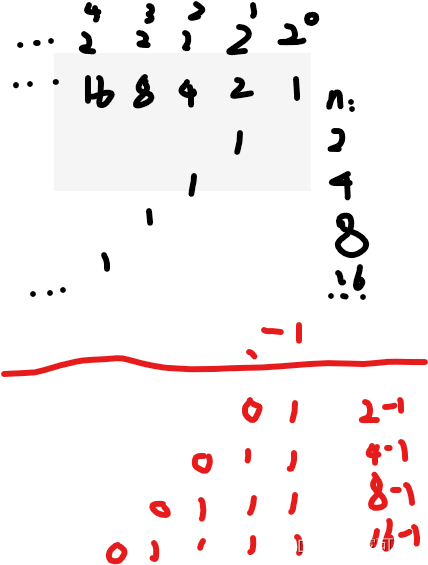
这时候n & (n-1) = ?
n & (n-1) = 0
是不是达成的效果跟n & (!n) = 0一样？

这就是2的幂次特殊的地方
记住了
我们如何判断数字n是2的幂次？
就用n&(n-1)=0来判断？n&(n-1)=0即2的n次幂，否则就不是

为啥不用n & (!n) = 0来判断嗯？你扯淡呢？
任何数字n与n取反相与不都是0吗？我举着例子只是想说明n&(n-1)=0达成的效果是n & (!n) = 0
不是让你用n & (!n) = 0来判断：n是否为2的幂次

---

总结

提示：重要经验：

1）n&(n-1)=0，说明n是2的幂次方
2）位运算速度快，很巧
3）笔试求AC，可以不考虑空间复杂度，但是面试既要考虑时间复杂度最优，也要考虑空间复杂度最优。