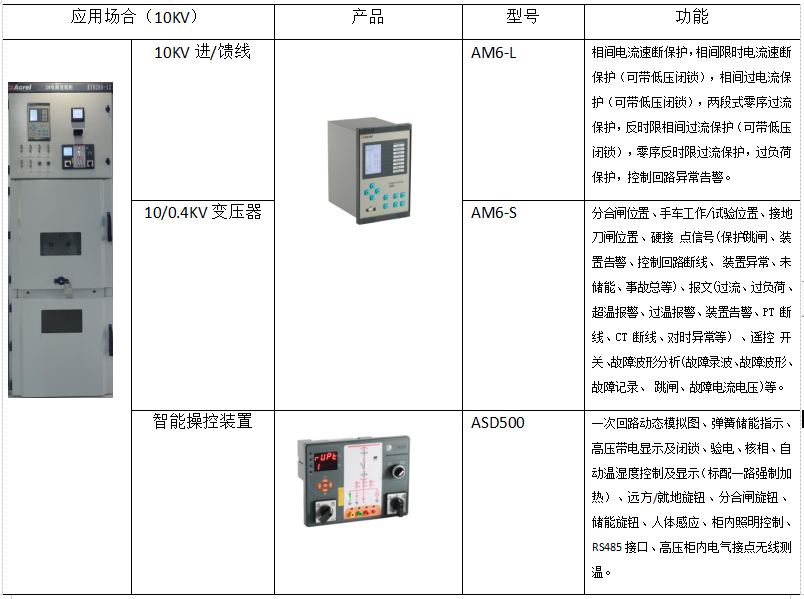
试题 A: 特殊日期
本题总分:5 分
【问题描述】 记一个日期为 yy 年 mm 月 dd 日,统计从 2000 年 1 月 1 日到 2000000 年 1 月 1 日,有多少个日期满足年份 yy 是月份 mm 的倍数,同时也是 dd 的倍数。
【答案提交】 这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一 个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
下面是我自己的提交,目前不知道正确答案是什么。
def run(x):if(x%100!=0 and x%4==0 ):return 1elif x%400==0:return 1return 0yrun=[31,29,31,30,31,30,31,31,30,31,30,31]
norun=[31,28,31,30,31,30,31,31,30,31,30,31]
msum=0for i in range(2000,2000001):for j in range(1,13):if i%j!=0:continueif(run(i)):for k in range(1,13):for s in range(1,yrun[k-1]):if(i%s==0):msum+=1else:for k in range(1,13):for s in range(1,norun[k-1]):if(i%s==0):msum+=1print(msum)
#426401585
试题 B: 分糖果
本题总分:5 分
【问题描述】 两种糖果分别有 9 个和 16 个,要全部分给 7 个小朋友,每个小朋友得到 的糖果总数最少为 2 个最多为 5 个,问有多少种不同的分法。 只要有其中一个小朋友在两种方案中分到的糖果不完全相同,这两种方案 就算作不同的方案。
【答案提交】 这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一 个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
没做出来,暂时先放着
试题 C: 三国游戏 (10分)
题目描述
小蓝正在玩一款游戏。游戏中魏蜀吴三个国家各自拥有一定数量的士兵X, Y, Z (一开始可以认为都为 0 )。游戏有 n 个可能会发生的事件,每个事件之间相互独立且最多只会发生一次,当第 i 个事件发生时会分别让 X, Y, Z 增加Ai , Bi ,Ci 。
当游戏结束时 (所有事件的发生与否已经确定),如果 X, Y, Z 的其中一个大于另外两个之和,我们认为其获胜。例如,当 X > Y + Z 时,我们认为魏国获胜。小蓝想知道游戏结束时如果有其中一个国家获胜,最多发生了多少个事件?
如果不存在任何能让某国获胜的情况,请输出 −1 。
输入格式
输入的第一行包含一个整数 n 。
第二行包含 n 个整数表示 Ai,相邻整数之间使用一个空格分隔。
第三行包含 n 个整数表示 Bi,相邻整数之间使用一个空格分隔。
第四行包含 n 个整数表示 Ci,相邻整数之间使用一个空格分隔。
输出格式
输出一行包含一个整数表示答案。
样例输入
3
1 2 2
2 3 2
1 0 7
没做出来,空着
试题D -平均 (10分)
有一个长度为 n 的数组(n 是 10 的倍数),每个数 ai 都是区间 [0, 9] 中的整数。小明发现数组里每种数出现的次数不太平均,而更改第 i 个数的代价为bi,他想更改若干个数的值使得这 10 种数出现的次数相等(都等于n/10),请问代价和最少为多少。
输入格式
输入的第一行包含一个正整数 n 。
接下来 n 行,第 i 行包含两个整数 ai , bi ,用一个空格分隔。
输出格式
输出一行包含一个正整数表示答案。
样例输入
10
1 1
1 2
1 3
2 4
2 5
2 6
3 7
3 8
3 9
4 10
应该说就是模拟题, 根据题目意思,贪心一下就行。
每次修改代价最小的数字就行。 不难
n=int(input())
arr=[0]*10
ave=n//10
sr=[[] for i in range(10)]
for i in range(n):a,d=map(int,input().split())arr[a]+=1sr[a].append(d)
price=0
for i in range(10):b=[]if(arr[i]>ave):b=sr[i]b.sort()price+=sum(b[:arr[i]-ave])
print(price)
"""
10
1 3
1 2
1 1
2 4
2 5
2 6
3 9
3 7
3 8
4 10
"""
可以通过全部测试点。
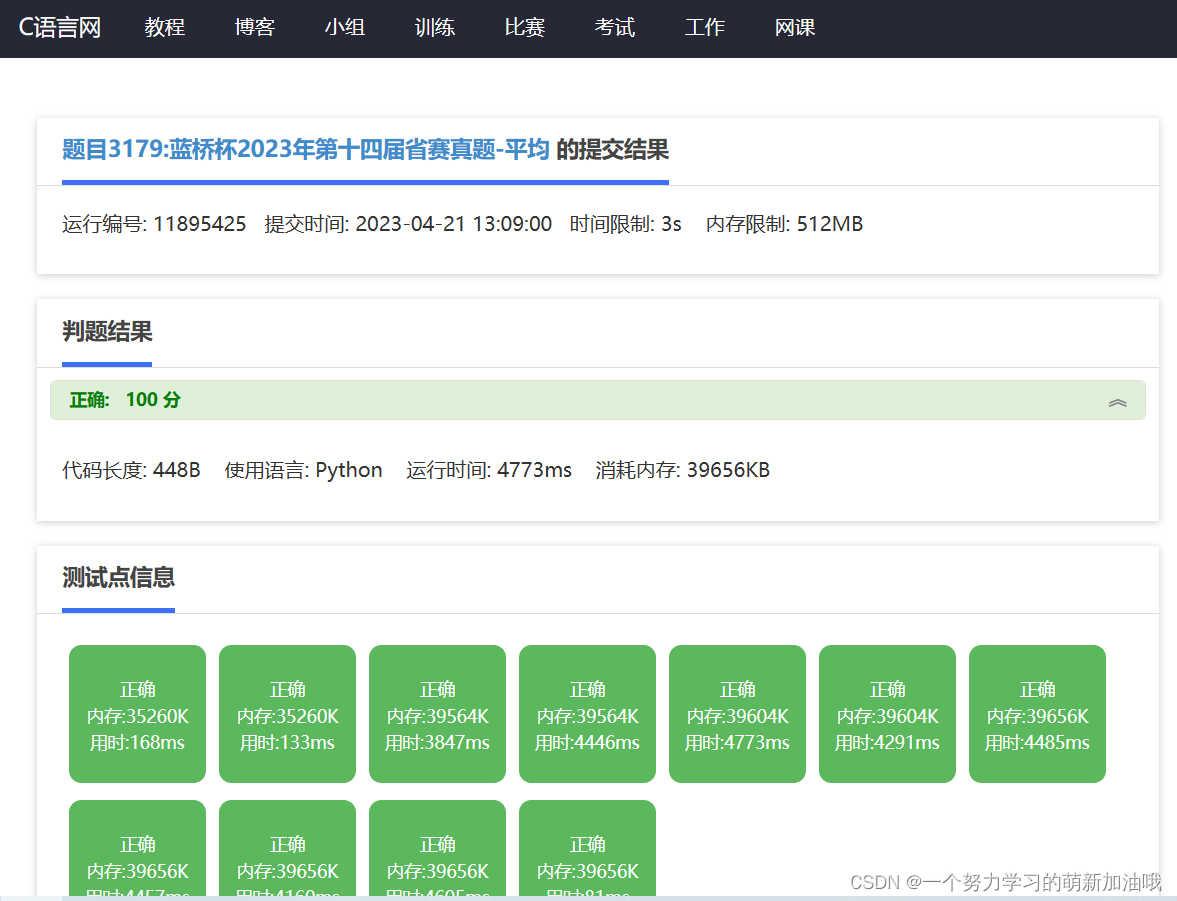
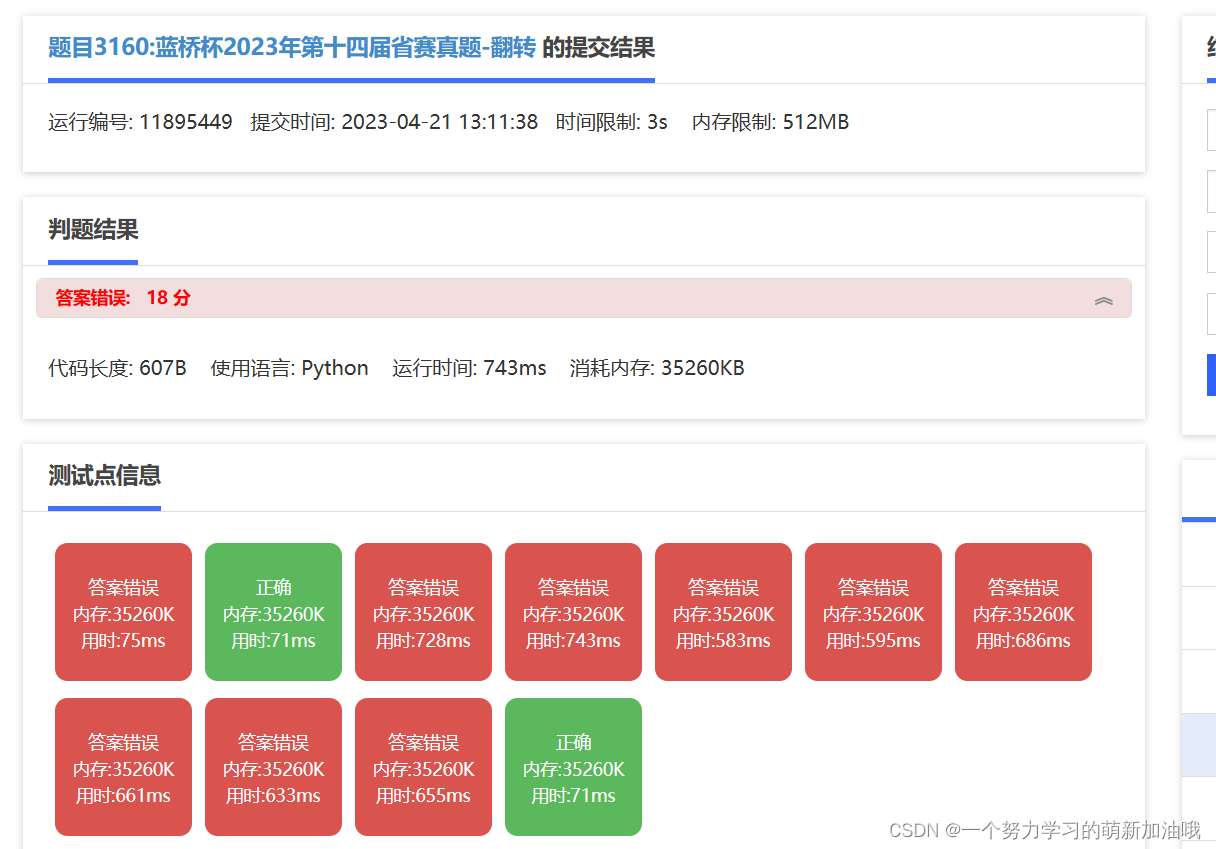
试题E -翻转 (也是模拟, 但是比赛的时候,没找对规律,只能过两个测试点) (15分)(只拿到2.3分)
小蓝用黑白棋的 n 个棋子排成了一行,他在脑海里想象出了一个长度为 n 的 01 串 T,他发现如果把黑棋当做 1,白棋当做 0,这一行棋子也是一个长度为 n 的 01 串 S。
小蓝决定,如果在 S 中发现一个棋子和它两边的棋子都不一样,就可以将其翻转变成另一个颜色。也就是说,如果 S 中存在子串 101 或者 010,就可以选择将其分别变为 111 和 000,这样的操作可以无限重复。
小蓝想知道最少翻转多少次可以把 S 变成和 T 一模一样。
输入格式
输入包含多组数据。
输入的第一行包含一个正整数 D 表示数据组数。
后面 2D 行每行包含一个 01 串,每两行为一组数据,第 2i − 1 行为第 i 组
数据的 Ti,第 2i 行为第 i 组数据的 Si,Si 和 Ti 长度均为 ni。
输出格式
对于每组数据,输出一行包含一个整数,表示答案,如果答案不存在请输出 −1。
样例输入
2
1000111
1010101
01000
11000
样例输出
2
-1
提示
对于 20% 的评测用例,1 ≤∑D1 ni ≤ 10 ;
对于所有评测用例,保证 1 ≤∑D1 ni ≤ 106 ,ni > 0 。
num=0 #这里错了,应该放到下面for循环里面的,每次都要重新计数。
不过改了之后,还是只能通过2个测试点。所以没啥用。
n=int(input())
num=0 #这里错了,应该放到下面for循环里面的,每次都要重新计数,真的很气
for i in range(n):T=list(input())S=list(input())if(len(S)!=len(T)):print(-1)continueif(S[0]!=T[0] or S[len(S)-1]!=T[len(T)-1]):print(-1)continuefor j in range(len(S)):if(S[j]!=T[j]):if(j>=1 and j<len(S)-1):if(S[j-1]!=S[j] and S[j+1]!=S[j] and S[j-1]==S[j+1]):num+=1print(num)
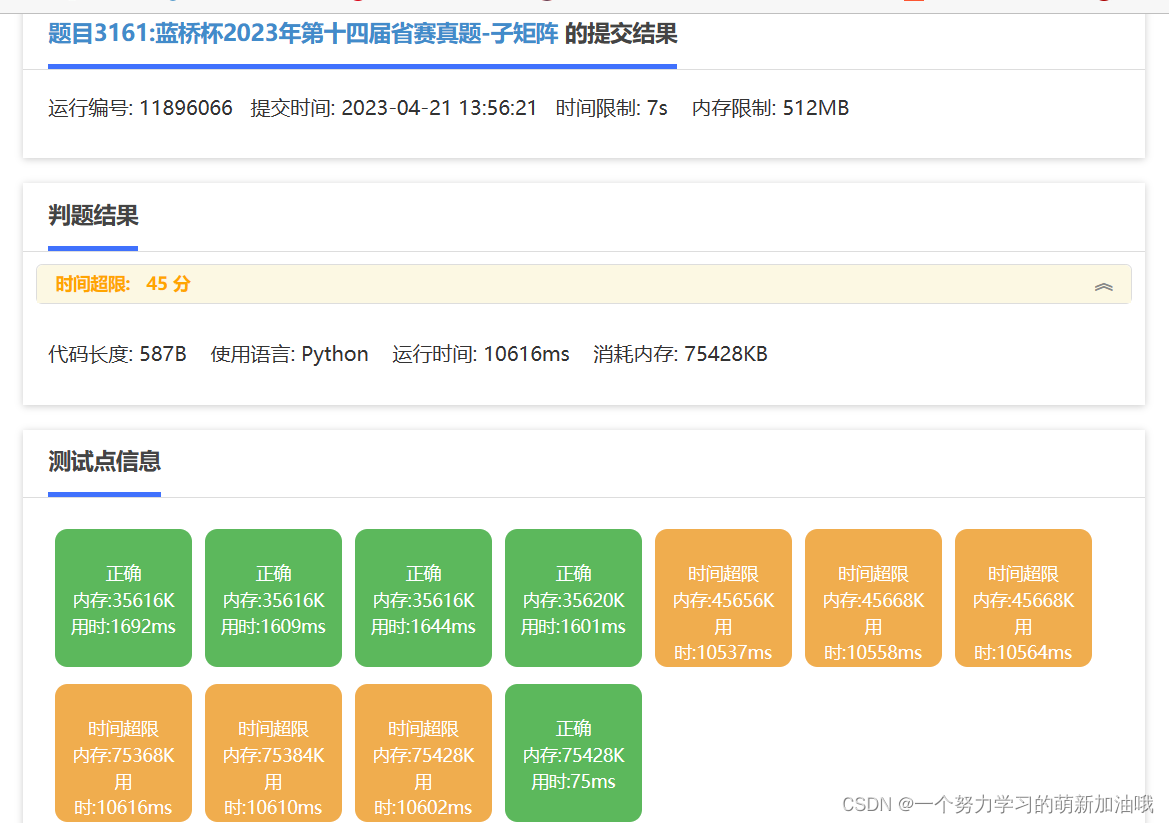
试题F 子矩阵 (忘记取模了, 真离谱,下次注意。) 15分 (只拿了1.3分)
给定一个 n × m (n 行 m 列)的矩阵。
设一个矩阵的价值为其所有数中的最大值和最小值的乘积。求给定矩阵的所有大小为 a × b (a 行 b 列)的子矩阵的价值的和。
答案可能很大,你只需要输出答案对 998244353 取模后的结果。
输入格式
输入的第一行包含四个整数分别表示 n, m, a, b ,相邻整数之间使用一个空格分隔。
接下来 n 行每行包含 m 个整数,相邻整数之间使用一个空格分隔,表示矩阵中的每个数 Ai, j 。
输出格式
输出一行包含一个整数表示答案。
样例输入
2 3 1 2
1 2 3
4 5 6
样例输出
58
提示
1×2+2×3+4×5+5×6 = 58 。
对于 40% 的评测用例,1 ≤ n, m ≤ 100 ;
对于 70% 的评测用例,1 ≤ n, m ≤ 500 ;
对于所有评测用例,1 ≤ a ≤ n ≤ 1000 1 ≤ b ≤ m ≤ 1000 1 ≤ Ai, j ≤ 109 。
暴力解法:
n,m,a,b=map(int,input().split())
#print(n,m,a,b)
arr=[]def mi_max(x,y):mmin=arr[x][y]mmax=arr[x][y]for i in range(a):for j in range(b):if(arr[x+i][y+j]<mmin):mmin=arr[x+i][y+j]if(arr[x+i][y+j]>mmax):mmax=arr[x+i][y+j]return mmin*mmaxfor i in range(n):k=list(map(int,input().split()))arr.append(k)
msum=0
for i in range(n-a+1):for j in range(m-b+1):msum+=mi_max(i,j)
print(msum%998244353 )
就过了暴力的测试点
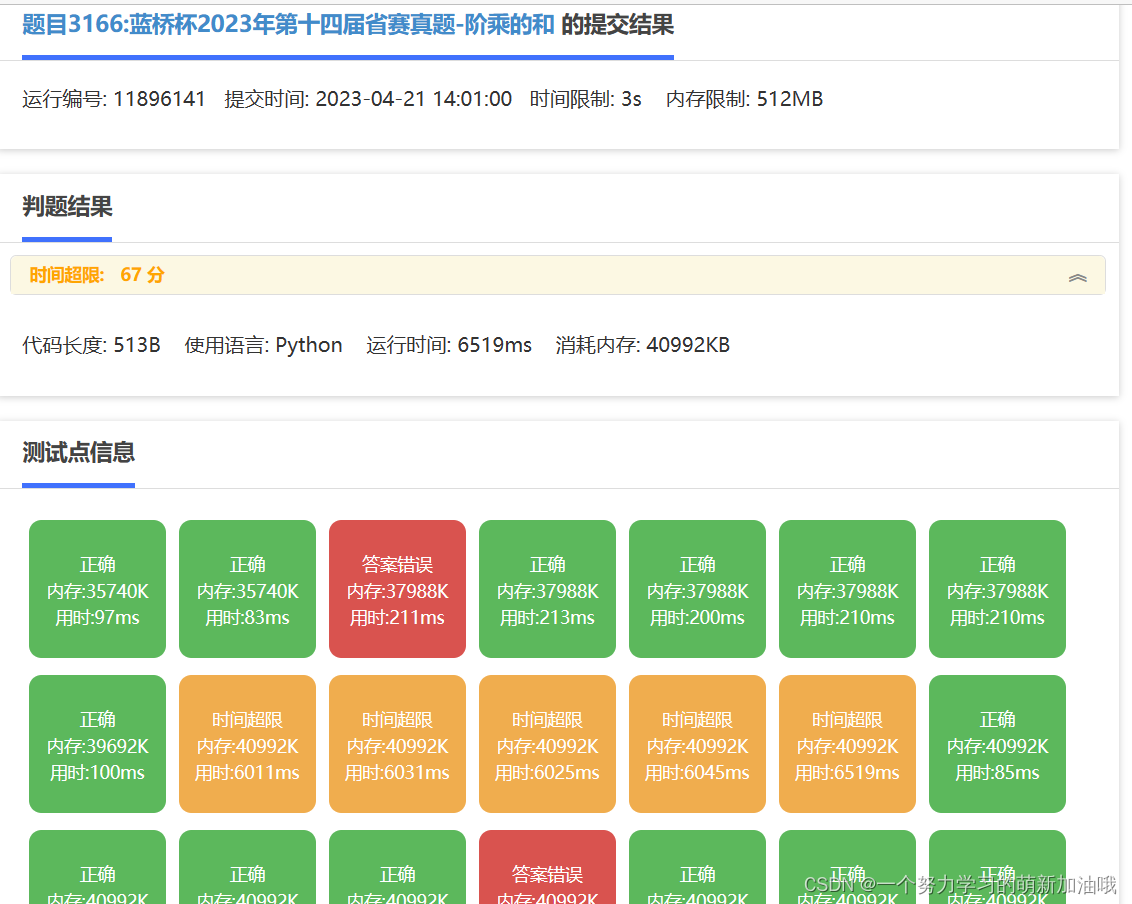
试题G 阶乘的和 (20分) (按下面结果显示拿了13.6分)
题目描述
给定 n 个数 Ai,问能满足 m! 为∑ni=1(Ai!) 的因数的最大的 m 是多少。其中 m! 表示 m 的阶乘,即 1 × 2 × 3 × · · · × m。
输入格式
输入的第一行包含一个整数 n 。
第二行包含 n 个整数,分别表示 Ai,相邻整数之间使用一个空格分隔。
输出格式
输出一行包含一个整数表示答案。
样例输入
3
2 2 2
样例输出
3
提示
对于 40% 的评测用例,n ≤ 5000 ;
对于所有评测用例,1 ≤ n ≤ 105 1 ≤ Ai ≤ 109 。
n=int(input())
def jie(n):global mminms=1for i in range(mmin+1,n+1):ms=i*msreturn msmsum=0
s=list(map(int, input().split()))
mmin=min(s)for j in range(n):if(s[j]==mmin):msum+=1continuemsum+=jie(s[j])#print(msum)
m=mmin
mmin=mmin+1
while msum>0:if(msum%mmin==0):m=mminmmin+=1msum=msum//mminelse:break
print(m)