为了减小机器人加速过程的冲击，这里梳理一下S形加减速相关知识。

1. S加减速曲线

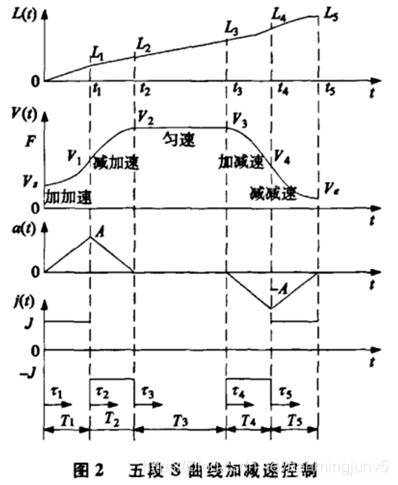
计算公式：
加加速度

$$j(t)=\{\begin{array}{ll}J& 0\le t\le t_1\\ -J& t_1\le t\le t_2\\ 0& t_2\le t\le t_3\\ -J& t_3\le t\le t_4\\ J& t_4\le t\le t_5\end{array}$$

加速度：

$$a(t)=\{\begin{array}{ll}J\ast t& 0\le t\le t_1\\ J\ast T_1-J\ast (t-t_1)& t_1\le t\le t_2\\ 0& t_2\le t\le t_3\\ -J\ast (t-t_3)& t_3\le t\le t_4\\ -J\ast T_4+J\ast (t-t_4)& t_4\le t\le t_5\end{array}$$

速度：

$$v(t)=\{\begin{array}{ll}{v}_s+J\ast t^2/2& 0\le t\le t_1\\ v_1+J\ast T_1\ast (t-t_1)-J\ast (t-t_1{)}^2/2& t_1\le t\le t_2\\ v_2& t_2\le t\le t_3\\ v_3-J\ast (t-t_3{)}^2/2& t_3\le t\le t_4\\ v_4-J\ast T_4\ast (t-t_4)+J\ast (t-t_4{)}^2/2& t_4\le t\le t_5\end{array}$$

位移：

​
$$s(t)=\{\begin{array}{ll}{v}_s\ast t+J\ast t^3/6& 0\le t\le t_1\\ s_1+v_1\ast (t-t_1)+J\ast T_1\ast (t-t_1{)}^2/2-J\ast (t-t_1{)}^3/6& t_1\le t\le t_2\\ s_2+v_2\ast (t-t_2)& t_2\le t\le t_3\\ s_3+v_3\ast (t-t_3)-J\ast (t-t_3{)}^3/6& t_3\le t\le t_4\\ s_4+v_4\ast (t-t_4)-J\ast T_4\ast (t-t_4{)}^2/2+J\ast (t-t_4{)}^3/6& t_4\le t\le t_5\end{array}$$

2. 算法流程（vs=0, ve=0）

已知 位移S，最大速度V 加加速度J，按照如下流程进行速度规划：

第一步，计算加速减速距离：

$$S_a=S_d=V\ast \sqrt{\frac{V}{J}}$$

第二步，比较位移关系

$$\begin{gathered} 如果S_a+S_d<=S \\ 则： \\ {t}_1=t_2=t_4=t_5=\sqrt{\frac{V}{J}} \\ {t}_3=\frac{S-S_a-S_d}{V} \end{gathered}$$

$$\begin{gathered} 如果S_a+S_d>S \\ 则： \\ {V}^{,}=(\frac{S\ast J}{2}{)}^{\frac{1}{3}} \\ {t}_1=t_2=t_4=t_5=\sqrt{\frac{V^{,}}{J}} \\ {t}_3=0 \end{gathered}$$

第三步，即得到每阶段对应的插补时间，即可进行速度插补

3. 算法流程（vs>0或 ve>0）

已知 位移S，起始速度Vs,终止速度Ve,最大速度V 加加速度J，按照如下流程进行速度规划：

第一步，计算加速减速距离：

$$\begin{gathered} S_a=(V+V_s)\ast \sqrt{\frac{V-V_s}{J}} \\ {S}_d=(V+V_e)\ast \sqrt{\frac{V-V_e}{J}} \end{gathered}$$

第二步，比较位移关系

$$\begin{gathered} 如果S_a+S_d<=S \\ 则： \\ {t}_1=t_2=\sqrt{\frac{V-V_s}{J}} \\ {t}_4=t_5=\sqrt{\frac{V-V_e}{J}} \\ {t}_3=\frac{S-S_a-S_d}{V} \end{gathered}$$

如果 	S_a + S_d > S 
重新计算最大速度V,因为解析解计算复杂，这里通过二分法逼近，方法如下：

(1)设置v1 = V,v2设置为Vs,Ve中较大的数值

(2)二分法计算最大速度

$$V=\frac{v1+v2}{2}$$

(3)计算加减速距离

$$\begin{gathered} S_a=(V+V_s)\ast \sqrt{\frac{V-V_s}{J}} \\ {S}_d=(V+V_e)\ast \sqrt{\frac{V-V_e}{J}} \end{gathered}$$

(3)比较位移

$$\begin{gathered} 如果S>S_a+S_d \\ 则： \\ v2=V如果S<S_a+S_d \\ 则： \\ v1=V \end{gathered}$$

(4) 重复步骤(1)(2)(3),直到

$$|S-S_a-S_d|<ϵ$$

阈值ε根据实际需求进行设置，通常设置为0.000001，迭代次数不超过10次.