floyd算法是求最短路径的算法,算法复杂度为n(o^3),其优点在于能够一次求解所有点到其他点的最短路径,不需要其他运算,使用二维数组存储。其三层循环自外向内分别为:中间点,起始点和终点。状态方程为:
num[i][j]=min(num[i][j],num[i][k]+num[k][j]);
num[j][i]=num[i][j]; /*在num[i][j]发生变化时num[j][i]要同时改变,如果不是图而是网的话不需要改变*/
注:num初值设定为点与点的邻接矩阵。
代码:
#include<bits/stdc++.h>
using namespace std;
int num[105][105];
int main(){int n=5,m=6; /*点数和边数,可以随意设置,下附该代码的测试样例*/for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){num[i][j]=0x3f3f3f3f;}}for(int i=1;i<=n;i++)num[i][i]=0; /*自己到自己一定是0*/for(int i=1;i<=m;i++){int x,y,l;cin>>x>>y>>l;num[x][y]=l;num[y][x]=l;}for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){num[i][j]=min(num[i][j],num[i][k]+num[k][j]);num[j][i]=num[i][j];}}}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(num[i][j]==0x3f3f3f3f)cout<<"-1"<<" ";else cout<<num[i][j]<<" ";}cout<<endl;}system("pause");return 0;
}
/*
1 5 3
1 2 5
2 3 1
5 3 4
3 4 2
4 5 7
*/注:点和点在初始状态下未邻接(不连通)时,应给一个极大值,一般用1e9或0x3f3f3f3f,不建议使用0或者负数,因为这样需要在进行状态转移增加判断,而如果设置成一个极大值可以直接用algorithm头文件里的min函数直接进行赋值。
区间DP是动态规划的一种,又称为合并类动态规划,是线性动态规划的扩展,它在分阶段地划分问题时,与阶段中元素出现的顺序和由前一阶段的区间中哪些元素合并而来有很大的关系。时间复杂度也为n(o^3),其三层循环分别为:步长,起始点,终点。而步长的作用是用来挑选起始点和终点之间的任意一点,这方面和Floyd有点像,但是区别是这个中间点服从 i<k<j。而Floyd可以是任何一点。

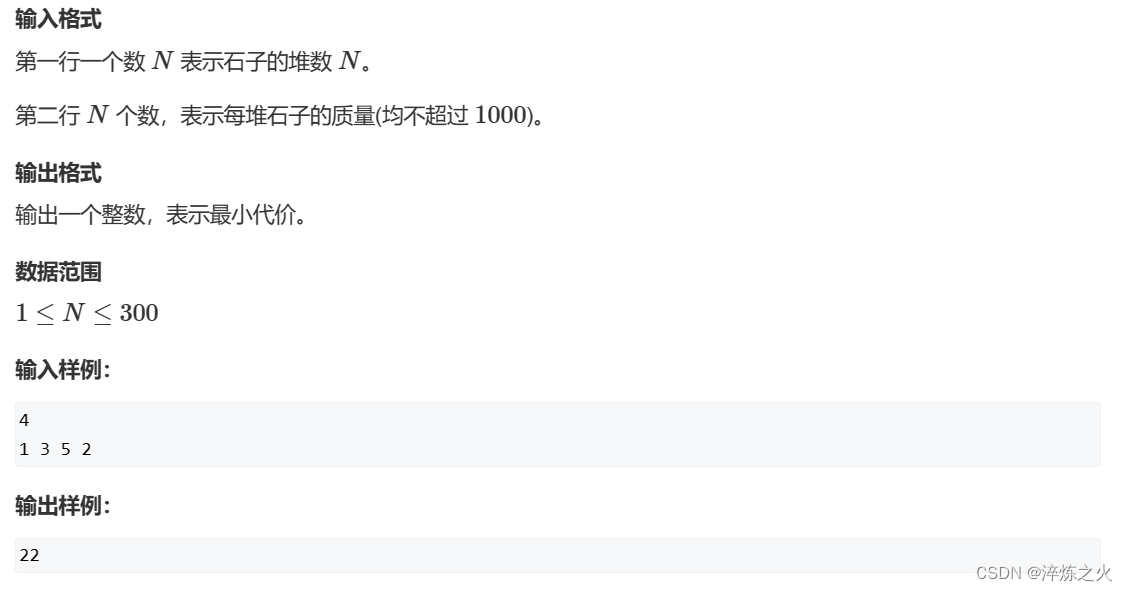
其状态转移方程为:
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+num[j]-num[i-1]);
注:num是每个点的权值的前缀和数组,dp是点与点合并的值
代码:
#include<bits/stdc++.h>
#define maxsize 305
using namespace std;
int dp[maxsize][maxsize];
int num[maxsize]={0};
int main(){int n;cin>>n;memset(dp,0x3f3f3f3f,sizeof(dp));for(int i=1;i<=n;i++){cin>>num[i];num[i]+=num[i-1];dp[i][i]=0;}for(int d=1;d<n;d++){for(int i=1;i<=n-d;i++){int j=i+d;for(int k=i;k<j;k++){dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+num[j]-num[i-1]);}}}cout<<dp[1][n];system("pause");return 0;
}总结:
floyd和区间dp并不完全一致,本人在做题的时候因为用了区间dp的状态转移方程踩了这个坑。另外两者存储方式上floyd可以直接在邻接矩阵上操作,而区间dp是先走一维,再走二维,操作上也并不完全一致。