文章目录
- 前言
- Task 1 商户位置点查询
- 题面
- 思路设计
- 实现代码
- hash_(sequential / binary)_search
- Binary_search_tree
- 数据分析
- Task 2 t o p − k top-k top−k 商户查询
- 题面
- 思路设计
- 实现代码
- 书本排序算法
- shell_sort
- heap_sort
- quick_sort
- 快速选择
- BFPTR
- 优先队列
- 注意事项
- 数据分析
- 小结
- 参考资料
- 补充
前言
主要的内容,代码都是课堂上讲过的,贴就好了。
Task 1 商户位置点查询
题面
单点时限: 24.0 sec
内存限制: 2048 MB
随着智能手机的普及,地理信息在诸如高德地图、大众点评、饿了么等App中得到广泛的应用,此次数据结构与算法课程期末大作业将模拟实际生活中的查询需求,完成基于地理信息和文本信息的查找任务。
系统中的每家商户包括以下3项内容:
1.位置 ( x , y ) (x,y) (x,y), x > 0 x>0 x>0, y > 0 y>0 y>0;
2.商家名称, 12 12 12位 A − Z A-Z A−Z字符串,不含小写;
3.菜系, 6 6 6位字符串 A − Z A-Z A−Z,不含小写;
查询功能为:用户输入自己感兴趣的商家名称如KFC,程序输出KFC的位置信息。在此保证查询成功时结果唯一,当查询的信息不存在时,查询失败,输出NULL。
输入格式
第 1 1 1行:商户的数量 m m m和查询的数量 n n n, m m m和 n n n为整数,均不超过 1 0 9 10^9 109;
第 2 − ( m + 1 ) 2-(m+1) 2−(m+1)行:商户的信息,包括商家名称,位置 x x x,位置 y y y和菜系;
最后的 n n n行:查询的信息,即每行包括一家商户的名称;
输出格式
输出应该为 n n n行,每一行对应于每次查询的结果,即商户的位置 x , y x,y x,y。
样例
| i n p u t input input |
|---|
| 5 3 JEANGEORGES 260036 14362 FRENCH HAIDILAO 283564 13179 CHAFINGDIS KFC 84809 46822 FASTFOOD SAKEMATE 234693 37201 JAPANESE SUBWAY 78848 96660 FASTFOOD HAIDILAO SAKEMATE SUBWAY |
| o u t p u t output output |
| 283564 13179 234693 37201 78848 96660 |
思路设计
首先将任务分解为:存储和查找。
-
存储
若完全采用顺序存储,则在查找时需要经历到的元素很多。在此考虑用类似链地址法解决冲突的哈希表的算法。建立一个 vector 数组,利用哈希函数得到每一个餐馆名称对应的索引值,再将餐馆信息存进这个 vector。相当于是一个个贴了餐馆对应的值的桶。 -
查找
定位到输入的餐馆名对应的 vector 数组,此时需要遍历的元素数量已经减少,可 以在此基础上使用顺序查找。 -
若要进行二分查找,则需要 vector 有序,需要写一个顺序插入的实现。
-
可以以餐馆名为关键字,采用 BST 来存储和查找。
实现代码
- 商户信息存储及符号重载
#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ULL;
enum Error_code{not_present,overflow,duplicate_error,success,underflow};struct info //店家信息
{int lx,ly;string name,style;info(string &sname,int &llx,int &lly,string &sstyle); info(const info &p);
};
bool operator > (const info &x, const info &y);
bool operator < (const info &x, const info &y);
bool operator <= (const info &x, const info &y);
ostream & operator << (ostream &output, info &a);info::info(const info &p)
{lx=p.lx;ly=p.ly;name=p.name;style=p.style;
}info::info(string &sname,int &llx,int &lly,string &sstyle)
{lx=llx;ly=lly;name=sname;style=sstyle;
}bool operator < (const info &x, const info &y)
{return x.name < y.name;
}bool operator > (const info &x, const info &y)
{return x.name>y.name;
}bool operator <= (const info &x, const info &y)
{return x.name<=y.name;
}ostream & operator << (ostream &output, info &a)
{output<< a.lx << " " << a.ly;return output;
}
hash_(sequential / binary)_search
- 答案类的定义
const int hash_size=9997;
class Solution
{public:Solution();void just_do_it_sequential_search(); //顺序查找void just_do_it_binary_search(); //二分查找private:string target; //待查找的目标ULL use_probe; //目标对应的hash值vector<info> entry[hash_size]; protected:void sequential_search();ULL hash_position(const string &new_entry) const; //计算映射值void init(string s_target); //获取需要查找的餐馆信息void append(info a); void orded_insert(info a); //顺序插入,二分查找用void recursive_binary_search(int bottom, int top, int &position);void recursive_binary_search_2(int bottom, int top, int &position);
};- 查找的实现
//顺序查找
void Solution::just_do_it_sequential_search()
{//ifstream in("rand_800000_10.in");int m,n;cin >> m >> n;//in >> m >> n;for(int i=0;i<m;i++){string name,style;int lx,ly;cin >> name >> lx >> ly >> style;//in >> name >> lx >> ly >> style;append(info(name,lx,ly,style));}for(int i=0;i<n;i++){string find;cin >> find;//in >> find;init(find);sequential_search();}
}void Solution::sequential_search()
{int len_entry;len_entry=entry[use_probe].size();for(int position=0;position<len_entry;position++){if(entry[use_probe][position].name==target){cout << entry[use_probe][position] << endl;return ;}}cout << "NULL" << endl;return ;
}
//二分查找
void Solution::orded_insert(info a)
{ULL probe=hash_position(a.name);if(entry[probe].size()==0){entry[probe].push_back(a);return ;}else if(a<entry[probe].front()){entry[probe].insert(entry[probe].begin(),a);return ;}else if(a>entry[probe].back()){entry[probe].push_back(a);}else{vector<info>::iterator it=entry[probe].begin();vector<info>::iterator temp;for (it; it!=entry[probe].end(); ++it){ temp=(it+1);if (*it<a&&a<=*temp){entry[probe].insert(it+1,a);break;}}return ;}
}void Solution::just_do_it_binary_search()
{//ifstream in("rand_800000_10.in");int m,n;cin >> m >> n;//in >> m >> n;for(int i=0;i<m;i++){string name,style;int lx,ly;cin >> name >> lx >> ly >> style;//in >> name >> lx >> ly >> style;orded_insert(info(name,lx,ly,style));}for(int i=0;i<n;i++){string find;cin >> find;//in >> find;init(find);int bottom=0;int top=entry[use_probe].size()-1;int position=-1;recursive_binary_search(bottom,top,position);//recursive_binary_search2(bottom,top,position);}
}void Solution::recursive_binary_search(int bottom, int top, int &position)
{ if (bottom<top) { int mid = (bottom+top)/2;if (target>entry[use_probe][mid].name) return recursive_binary_search(mid+1,top,position);else return recursive_binary_search(bottom,mid,position);}else {position=bottom; if (entry[use_probe][position].name == target) {cout << entry[use_probe][position] << endl;return ;}cout << "NULL" << endl;return ;}
}void Solution::recursive_binary_search_2(int bottom, int top, int &position)
{ if (bottom<=top) { int mid = (bottom+top)/2;if(target==entry[use_probe][mid].name){position=mid; cout << entry[use_probe][position] << endl;return ;}if (target>entry[use_probe][mid].name) return recursive_binary_search_2(mid+1,top,position);else return recursive_binary_search_2(bottom,mid-1,position);}else {cout << "NULL" << endl;return ;}
}
- 其他函数实现
Solution::Solution()
{}void Solution::init(string s_target)
{target=s_target;use_probe=hash_position(target);
}void Solution::append(info a)
{ULL probe=hash_position(a.name);entry[probe].push_back(a);
}ULL Solution::hash_position(const string &str) const
{ULL seed = 13;ULL hash = 0;for(int i=0;i<str.length();i++){hash = (hash*seed+(str[i]-'A'))%hash_size;}return hash;
}- main函数
int main()
{Solution s;s.just_do_it_sequential_search();return 0;
}
Binary_search_tree
- 二叉树结点
struct Binary_node
{info data;Binary_node *left;Binary_node *right;Binary_node( );Binary_node(const info &x);
};Binary_node :: Binary_node( )
{left = NULL;right = NULL;
}Binary_node :: Binary_node(const info &x)
{data = x;left = NULL;right = NULL;
}
- 二叉查找树
class Binary_search_tree
{public:Binary_search_tree( );Error_code insert(const info &new_data);Error_code tree_search(info &target) const;private:Binary_node *search_for_node(Binary_node* sub_root, const info &target) const;Error_code search_and_insert(Binary_node * &sub_root, const info &new_data);Binary_node *root;int count;
};Binary_search_tree::Binary_search_tree()
{root = NULL;count=0;
}Binary_node* Binary_search_tree::search_for_node(
Binary_node * sub_root, const info &target) const
{if (sub_root == NULL || sub_root->data == target)return sub_root;else if (sub_root->data < target)return search_for_node(sub_root->right, target);else return search_for_node(sub_root->left, target);
}Error_code Binary_search_tree::tree_search(info &target) const
{Error_code result = success;Binary_node *found = search_for_node(root,target);if (found == NULL)result = not_present;elsetarget = found->data;return result;
}Error_code Binary_search_tree::insert(const info &new_data)
{Error_code result=search_and_insert(root, new_data);if(result==success)count++;return result;
}Error_code Binary_search_tree::search_and_insert(
Binary_node * &sub_root, const info &new_data)
{if (sub_root == NULL) {sub_root = new Binary_node(new_data);return success;}else if (new_data < sub_root->data)return search_and_insert(sub_root->left, new_data);else if (new_data > sub_root->data)return search_and_insert(sub_root->right, new_data);else return duplicate_error;
}
- main函数
int main()//ifstream in("rand_4000_1.in");int m,n;cin >> m >> n;//in >> m >> n;//cout << "m = " << m << " n = " << n << endl;Binary_search_tree my_tree;for(int i=0;i<m;i++){string name,style;int lx,ly;cin >> name >> lx >> ly >> style;//in >> name >> lx >> ly >> style;my_tree.insert(info(name,lx,ly,style));}for(int i=0;i<n;i++){string find;cin >> find;//in >> find;info target(find);Error_code p;p=my_tree.tree_search(target);if(my_tree.tree_search(target)!=not_present)cout << target << endl;elsecout << "NULL" << endl;}return 0;
}
数据分析
统计了各算法在不同的数据规模(200,4000,800000)下,和不同数据特性(升序,降序,随机)下的查找时间。篇幅有限不展示全部测试数据。
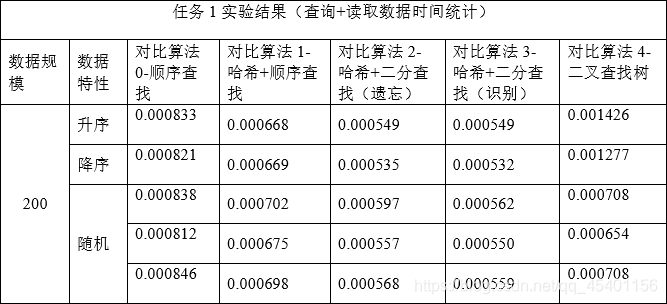
可视化处理:
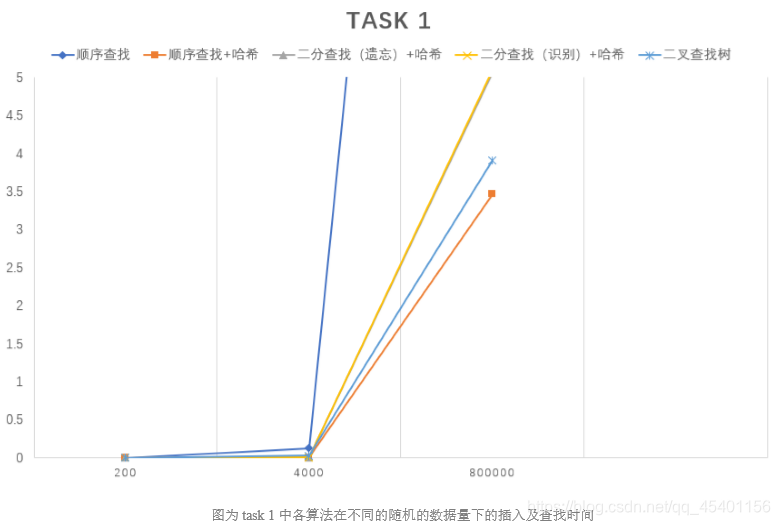
-
顺序查找:查找时间复杂度为O( n ),查找效率最低,耗时最长。
-
二分查找(健忘、识别):查找时间复杂度为O(log(n)),在实际使用过程中,两种二分查找的折线几乎重合。因为算法要求数组有序,在插入的时候设计了线性查找大小的插入算法,导致
(a) 在数据量较小时(200)建立二分查找的系统开销和额外的程序设计强度使得使用它比使用顺序查找代价更大;
(b) 当输入数据有序时插入速度更快。 -
二叉查找树:查找时间复杂度最坏情况为O(n),最好情况为O(log(n)),在输入数据有序的情况下退化为链表的顺序查找。
-
哈希+顺序查找:插入、访问和查找的时间复杂度最好均为O(1),最坏均为O(n)。速度极大加快,查找耗时最短。
Task 2 t o p − k top-k top−k 商户查询
题面
单点时限: 29.0 sec
内存限制: 2048 MB
随着智能手机的普及,地理信息在诸如高德地图、大众点评、饿了么等App中得到广泛的应用,此次数据结构课程期末大作业将模拟实际生活中的查询需求,完成基于地理信息和文本信息的查找任务。
系统中每家商户包含以下3项信息:
1.位置 ( x , y ) (x,y) (x,y), x > 0 x>0 x>0, y > 0 y>0 y>0;
2.商家名称, 12 12 12位 A − Z A-Z A−Z字符串,不含小写;
3.菜系, 6 6 6位字符串 A − Z A-Z A−Z,不含小写;
你的程序需要提供给用户以下查询的功能:用户输入自己的位置点如 < u x , u y > <ux,uy> <ux,uy>、感兴趣的菜系和整数 k k k值,程序按照由近到远输出商家名称和距离,距离相等时以照商家名称的字典序为准。在此距离精确到小数点后的 3 3 3位(四舍五入)。若满足条件的商户不足 k k k个,则输出所有满足条件的商家信息。若存在一次查询中无任何满足条件的商户,则输出空行即可。
输入格式
第 1 1 1行:商户的数量 m m m和查询的数量 n n n, m m m和 n n n为整数,均不超过 1 0 9 10^9 109;
第 2 − ( m + 1 ) 2-(m+1) 2−(m+1)行:商户的信息,包括商家名称,位置 x x x,位置 y y y和菜系;
最后的 n n n行:每一行表示一次查询,包括用户的位置 u x ux ux和 u y uy uy、菜系名称、 k k k值;
输出格式
对应于每一次查询,按照顺序输出满足条件的商户信息,每一行对应于一家商户。
样例
| i n p u t input input |
|---|
| 5 2 MCDONALD 260036 14362 FASTFOOD HAIDILAO 283564 13179 CHAFINGDIS KFC 84809 46822 FASTFOOD DONGLAISHUN 234693 37201 CHAFINGDIS SUBWAY 78848 96660 FASTFOOD 28708 23547 FASTFOOD 2 18336 14341 CHAFINGDIS 3 |
| o u t p u t output output |
| KFC 60737.532 SUBWAY 88653.992 DONGLAISHUN 217561.327 HAIDILAO 265230.545 |
思路设计
-
因为输入数据是公开的,先测试一下数据规模
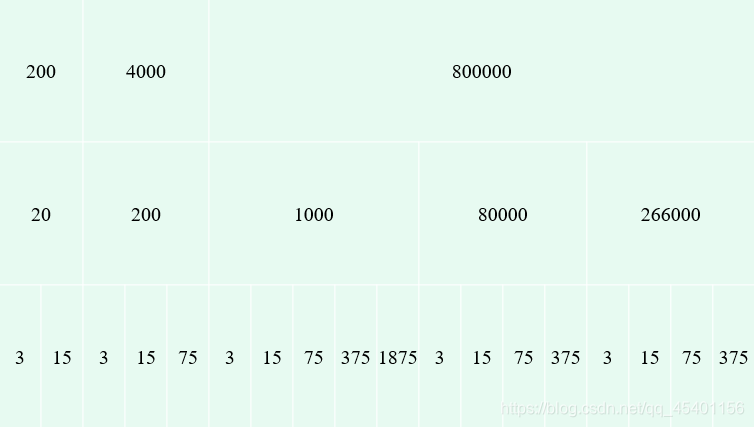
第一行为数据规模N,第二行为每个菜系包含的餐馆数量T,第三行为需要查询的K值。 -
考虑对数据全体排序

前三个时间复杂度为 O(n^2)的算法不考虑,仅考虑时间复杂度为 O(n log n)的,在最大数据规模 N=800000 下也很难在规定时间内完成查找,为了减少遍历所需元素,采用采用类似 Task 1 时使用的 hash_vector,以菜系作为关键字来存放参观数据。在此我采用的是希尔排序、快速排序和堆排序具体排序思路同书本。 -
Quick_select
减治法的一种,大体思路类似于 Quick_sort,但是只需要考虑一边。实现思路为
(1) 用 vector 存放所有数据
(2) 确认轴点 pivot,此处选用数组中最后一个该菜系的元素作为轴点
(3) Partition 过程大体类似于 quick_sort,把小于轴点的放在左边,大于轴点的放在 右边。
(4) 判断此时数组左边的长度 L,若 L 和 k 相等,表明全体元素中最小的 k 个已经被 找到;若 L > k,则将右边数据舍弃,继续调用 partition 在轴点左边进行划分; 若 L < k,则在右边继续 partition 划分,寻找最小的 L – k 个元素。
(5) 查找过程结束后,数组最左边的元素是符合要求的前 k 个最小的元素,但是他们之间是无序的,此时调用堆排序,排序后输出。
(6) 优化 1:采用类似 Task 1 时使用的 hash_vector,以菜系作为关键字来存放参观 数据,可以有效减少 partition 时需要遍历的元素个数,将时间复杂度优化为 O(T),经过实验可知采用好的哈希函数可以得到很高的命中率。
(7) 优化 2:挑选轴点的策略会影响算法的效率,查阅资料得知一种 bfprt 算法, 即:将所有数据分组之后取中位数再取中位数的中位数作为轴点。 -
BFPTR
在前面的快速选择算法中,我是选取最后一个该菜系的餐馆作为轴点,算法的效率和轴点的选取有很大关系。在BFPTR算法中,每次选择五份中位数的中位数作为pivot,这样做使得划分比较合理,从而避免了最坏情况( O ( n 2 ) O(n^2) O(n2))的发生。算法步骤如下:
(1)将输入数组的 n n n个元素划分为 n / 5 n/5 n/5组,每组 5 5 5个元素,且至多只有一个组由剩下的 n % 5 n\%5 n%5个元素组成。
(2)寻找 n / 5 n/5 n/5个组中每一个组的中位数,首先对每组的元素进行插入排序,然后从排序过的序列中选出中位数。
(3)对于(2)中找出的 n / 5 n/5 n/5个中位数,递归进行步骤(1)和(2),直到只剩下一个数即为这 n / 5 n/5 n/5个元素的中位数,找到中位数后并找到对应的下标 p p p。
(4)进行Partion划分过程,Partion划分中的pivot元素下标为 p p p。 -
优先队列
只需要对数据访问一次,非常快速且高效。通过对大根堆堆顶的改变来获取 前 k 个最小值。实现思路为:
(1) 用 vector 存放所有数据
(2) 从前往后从 vector 中取出 k 个餐馆的信息,建立一个大根堆。
(3) 继续向后遍历元素,若菜系相同且距离小于堆顶,则将堆顶替换成当前元素, 并重新整理大根堆。
(4) 最后将成堆做一次堆排序然后输出即可。
(5) 优化:采用类似 Task 1 时使用的 hash_vector,以菜系作为关键字来存放餐馆数据,可以有效减少 partition 时需要遍历的元素个数,经过实验可知采用好的哈希函数可以得到很高的命中率。
实现代码
- 商户信息存储及符号重载
#include<bits/stdc++.h>
using namespace std;
const double eps = 1e-4;
typedef unsigned long long ULL; struct info //店家信息
{double lx,ly,dis;string name,style;info(string &sname,double &llx,double &lly,string &sstyle); info(const info &p);
};
bool operator > (const info &x, const info &y);
bool operator < (const info &x, const info &y);
ostream & operator << (ostream &output, info &a);info::info(const info &p)
{lx=p.lx;ly=p.ly;name=p.name;style=p.style;dis=p.dis;
}info::info(string &sname,double &llx,double &lly,string &sstyle)
{lx=llx;ly=lly;name=sname;style=sstyle;dis=0.0;
}bool operator < (const info &x, const info &y)
{if(x.dis==y.dis)return x.name<y.name;return x.dis < y.dis;
}bool operator > (const info &x, const info &y)
{if(x.dis==y.dis)return x.name>y.name;elsereturn x.dis > y.dis;
}ostream & operator << (ostream &output, info &a)
{output<< a.name << " " << setiosflags(ios::fixed|ios::showpoint)<< setprecision(3) << a.dis;return output;
}
书本排序算法
- 答案类的定义
const int hash_size=9997;
class Solution
{public:Solution();void init(double num_x,double num_y,int num_k,string s_target); //每轮查询之前更新数据 void just_do_it();void append(info a); //加入信息 private:double use_x,use_y;int use_k;ULL use_probe;string target;vector<info> entry[hash_size];vector<info> out;protected:void search_print(); //打印结果 void distance(int position); //计算距离 ULL hash_position(const string &new_entry) const;void heap_sort(); //83void insert_heap(const info ¤t,int low,int high);void build_heap();void sort_interval(int start,int increment);void shell_sort(); //83int partition(int low,int high);void recursive_quick_sort(int low,int high);void quick_sort();//83
};
shell_sort
void Solution::shell_sort()
{int increment,start;increment=out.size();do{increment=increment/3+1;for(start=0;start<increment;start++)sort_interval(start,increment);}while(increment>1);
}void Solution::sort_interval(int start,int increment)
{int first_unsorted;int place;for (first_unsorted=start+increment;first_unsorted<out.size();first_unsorted+=increment) if(out[first_unsorted]<out[first_unsorted-increment]){place=first_unsorted;info current(out[first_unsorted]);do{out[place]=out[place-increment];place-=increment;}while(place>start&&out[place-increment]>current);out[place]=current;}
}
heap_sort
void Solution::heap_sort()
{int last_unsorted;build_heap();for(last_unsorted=out.size()-1;last_unsorted>0;last_unsorted--){info current(out[last_unsorted]);out[last_unsorted]=out[0];insert_heap(current,0,last_unsorted-1);}
}void Solution::insert_heap(const info ¤t,int low,int high)
{int large;large=2*low+1;while(large<=high){if(large<high&&out[large]<out[large+1])large++;if(current<out[large]){out[low]=out[large];low=large;large=2*low+1;}elsebreak;}out[low]=current;
}void Solution::build_heap()
{int low;for(low=out.size()/2-1;low>=0;low--){info current(out[low]);insert_heap(current,low,out.size()-1); }
}quick_sort
void Solution::recursive_quick_sort(int low,int high)
{int pivot_position;if(low<high){pivot_position=partition(low,high);recursive_quick_sort(low,pivot_position-1);recursive_quick_sort(pivot_position+1,high);}
}int Solution::partition(int low,int high)
{int i,last_small;swap(out[low],out[high]);info pivot(out[low]);last_small=low;for(int i=low+1;i<=high;i++){if(out[i]<pivot){last_small=last_small+1;swap(out[last_small],out[i]);}}swap(out[low],out[last_small]);return last_small;
}
- 其他函数实现
Solution::Solution()
{}void Solution::append(info a)
{ULL probe=hash_position(a.style);entry[probe].push_back(a);
}void Solution::distance(int position)
{double ans;ans=sqrt(fabs(entry[use_probe][position].lx-use_x)*fabs(entry[use_probe][position].lx-use_x)+fabs(entry[use_probe][position].ly-use_y)*fabs(entry[use_probe][position].ly-use_y));entry[use_probe][position].dis=round(ans*1000)/1000;
}void Solution::init(double num_x,double num_y,int num_k,string s_target)
{use_x=num_x;use_y=num_y;use_k=num_k;target=s_target;use_probe=hash_position(target);out.clear();
}void Solution::just_do_it()
{for(int i=0;i<entry[use_probe].size();i++)if(entry[use_probe][i].style==target){distance(i);out.push_back(entry[use_probe][i]);}int len=out.size();if(use_k>len)use_k=len;search_print();
}ULL Solution::hash_position(const string &str) const
{unsigned int seed = 1313;ULL hash = 0;for(int i=0;i<str.length();i++){hash = (hash*seed+(str[i]-'A'+1))%hash_size;}return hash;
}void Solution::search_print()
{quick_sort();//heap_sort()、shell_sort() int len_out=out.size();for(int i=0;i<len_out&&i<use_k;i++){cout << out[i] << endl;}
}- main函数
int main(int argc, char** argv)
{//ifstream in("800000_rand_query15times_2.in");int n,m;cin >> n >> m;//in >> n >> m;Solution s;for(int i=0;i<n;i++){double lx,ly;string name,style;cin >> name >> lx >> ly >> style;//in >> name >> lx >> ly >> style;s.append(info(name,lx,ly,style));}for(int i=0;i<m;i++){/*LARGE_INTEGER begin;LARGE_INTEGER end;LARGE_INTEGER frequ;QueryPerformanceFrequency(&frequ);QueryPerformanceCounter(&begin); //获取开始的时刻*/double lx,ly;int lk;string ltarget;cin >> lx >> ly >> ltarget >> lk;//in >> lx >> ly >> ltarget >> lk;s.init(lx,ly,lk,ltarget);s.just_do_it();/*cout << "k = " << lk << endl; QueryPerformanceCounter(&end);//获取结束的时刻cout<<fixed<<"time :"<<(end.QuadPart - begin.QuadPart)/(double)frequ.QuadPart<<endl;QueryPerformanceFrequency(&frequ);cout << endl;cin.get();*/}return 0;
}
快速选择
- 答案类的定义
const int hash_size=99997;
class Solution
{public:Solution();void init(double num_x,double num_y,int num_k,string s_target); //每轮查询之前更新数据 void append(info a); //加入信息 int partition(int low,int high);void topk(int low,int high,int k);void just_do_it();void search_print(); //打印结果 void distance(int position); //计算距离 ULL hash_position(const string &new_entry) const;void heap_sort();void insert_heap(const info ¤t,int low,int high);void build_heap();private:double use_x,use_y;int use_k;ULL use_probe;string target;vector<info> entry[hash_size];vector<info> res;vector<info> out;
};
- 快速选择的实现
void Solution::topk(int low,int high,int k)
{if(low<high){int pos=partition(low,high);if(pos==-1)return ;int len=pos-low+1;if(len==k)return ;else if(len<k)topk(pos+1,high,k-len);elsetopk(low,pos-1,k);}elsereturn ;
}int Solution::partition(int low,int high)
{int pivot_position=high;while(res[pivot_position].style!=target)pivot_position--;distance(pivot_position);info pivot(res[pivot_position]);int last_small;last_small=low;for(int i=low;i<pivot_position;i++){if(res[i].style==target){distance(i);if(pivot>res[i]){swap(res[last_small],res[i]);last_small++;}}}swap(res[pivot_position],res[last_small]);return last_small;
}
- 堆排序的实现(可选用其他排序)
void Solution::heap_sort()
{int last_unsorted;build_heap();for(last_unsorted=out.size()-1;last_unsorted>0;last_unsorted--){info current(out[last_unsorted]);out[last_unsorted]=out[0];insert_heap(current,0,last_unsorted-1);}
}void Solution::insert_heap(const info ¤t,int low,int high)
{int large;large=2*low+1;while(large<=high){if(large<high&&out[large]<out[large+1])large++;if(current<out[large]){out[low]=out[large];low=large;large=2*low+1;}elsebreak;}out[low]=current;
}void Solution::build_heap()
{int low;for(low=out.size()/2-1;low>=0;low--){info current(out[low]);insert_heap(current,low,out.size()-1); }
}
- 其他函数实现
Solution::Solution()
{}void Solution::append(info a)
{ULL probe=hash_position(a.style);entry[probe].push_back(a);
}void Solution::distance(int position)
{double ans;ans=sqrt(fabs(res[position].lx-use_x)*fabs(res[position].lx-use_x)+fabs(res[position].ly-use_y)*fabs(res[position].ly-use_y));res[position].dis=round(ans*1000)/1000;
}void Solution::init(double num_x,double num_y,int num_k,string s_target)
{use_x=num_x;use_y=num_y;use_k=num_k;target=s_target;use_probe=hash_position(target);out.clear();res.clear();
}void Solution::just_do_it()
{res.assign(entry[use_probe].begin(),entry[use_probe].end());int len=res.size();if(use_k>len)use_k=len;topk(0,len-1,use_k);search_print();
}
- 主函数同上
BFPTR
void Solution::just_do_it()
{for(int i=0;i<entry[use_probe].size();i++)if(entry[use_probe][i].style==target)res.push_back(entry[use_probe][i]);int len=res.size();if(use_k>len)use_k=len;int p=BFPRT( 0,len-1,use_k);search_print();
}int Solution::Insert_Sort(int left, int right) //插入排序
{int j;for (int i = left + 1; i <= right; i++){distance(i);info temp(res[i]);j = i - 1;while (j >= left && res[j] > temp){distance(j);distance(j+1);res[j + 1] = res[j];j--;}res[j + 1] = temp;}return ((right - left) >> 1) + left;
}int Solution::Get_Pivot_Index(int left, int right) //获取轴点
{if (right - left < 5)return Insert_Sort(left, right);int sub_right = left - 1;for (int i = left; i + 4 <= right; i += 5){int index = Insert_Sort(i, i + 4);swap(res[++sub_right], res[index]);}return BFPRT(left, sub_right, ((sub_right - left + 1) >> 1) + 1);
}int Solution::Partition(int left, int right, int pivot_index)
{swap(res[pivot_index], res[right]); // 把主元放置于末尾distance(right);int partition_index = left; // 跟踪划分的分界线for (int i = left; i < right; i++){distance(i);if (res[i] < res[right]){swap(res[partition_index++], res[i]); // 比主元小的都放在左侧}}swap(res[partition_index], res[right]); // 最后把主元换回来return partition_index;
}int Solution::BFPRT(int left, int right, int k) //高低分区查找
{int pivot_index = Get_Pivot_Index(left, right); // 得到中位数的中位数下标(即主元下标)int partition_index = Partition(left, right, pivot_index); // 进行划分,返回划分边界int num = partition_index - left + 1;if (num == k)return partition_index;else if (num > k)return BFPRT(left, partition_index - 1, k);elsereturn BFPRT(partition_index + 1, right, k - num);
}优先队列
- 答案类的定义
const int hash_size=9997;
class Solution
{public:Solution();void init(double num_x,double num_y,int num_k,string s_target); //每轮查询之前更新数据 void append(info a); //加入信息 void insert_heap(const info ¤t,int low,int high); //向堆中插入元素 void build_heap(); //建堆 void heap_sort(); //堆排序 void just_do_it(); //处理,挑选数据 void search_print(); //打印结果 void distance(int position); //计算距离 unsigned int hash_position(const string &new_entry) const;private:double use_x,use_y;int use_k;unsigned int use_probe;string target;vector<info> entry[hash_size];vector<info> res;
};
- 选取和排序的实现
void Solution::just_do_it()
{int len_entry=entry[use_probe].size();int cnt=0,flag;for(flag=0;flag<len_entry&&cnt<use_k;flag++){if(entry[use_probe][flag].style==target){distance(flag);res.push_back(entry[use_probe][flag]);cnt++;}}use_k=res.size();build_heap();for(int i=flag;i<len_entry;i++) //挑选比堆顶小的 {if(entry[use_probe][i].style==target){distance(i);if(res[0]>entry[use_probe][i]){res[0]=entry[use_probe][i];build_heap();}}}heap_sort();search_print();
}void Solution::build_heap()
{int low;for(low=use_k/2-1;low>=0;low--){info current(res[low]);insert_heap(current,low,use_k-1);}
}void Solution::insert_heap(const info ¤t,int low,int high)
{int large;large=2*low+1;while(large<=high){if(large<high&&res[large]<res[large+1])large++;if(current<res[large]){res[low]=res[large];low=large;large=2*low+1;}elsebreak;}res[low]=current;
}void Solution::heap_sort()
{int last_unsorted;for(last_unsorted=use_k-1;last_unsorted>0;last_unsorted--){info current(res[last_unsorted]);res[last_unsorted]=res[0];insert_heap(current,0,last_unsorted-1);}
}
- 其余函数和主函数同上。
注意事项
- 题目会卡精度,在计算距离的时候要注意四舍五入取三位小数
void Solution::distance(int position)
{double ans;ans=sqrt(fabs(entry[use_probe][position].lx-use_x)*fabs(entry[use_probe][position].lx-use_x)+fabs(entry[use_probe][position].ly-use_y)*fabs(entry[use_probe][position].ly-use_y));entry[use_probe][position].dis=round(ans*1000)/1000;
}
数据分析
统计了各算法在不同的数据规模,不同餐馆规模和不同 k k k值下的查找时间。篇幅有限不展示全部测试数据。(加了_hash即为使用hash优化)
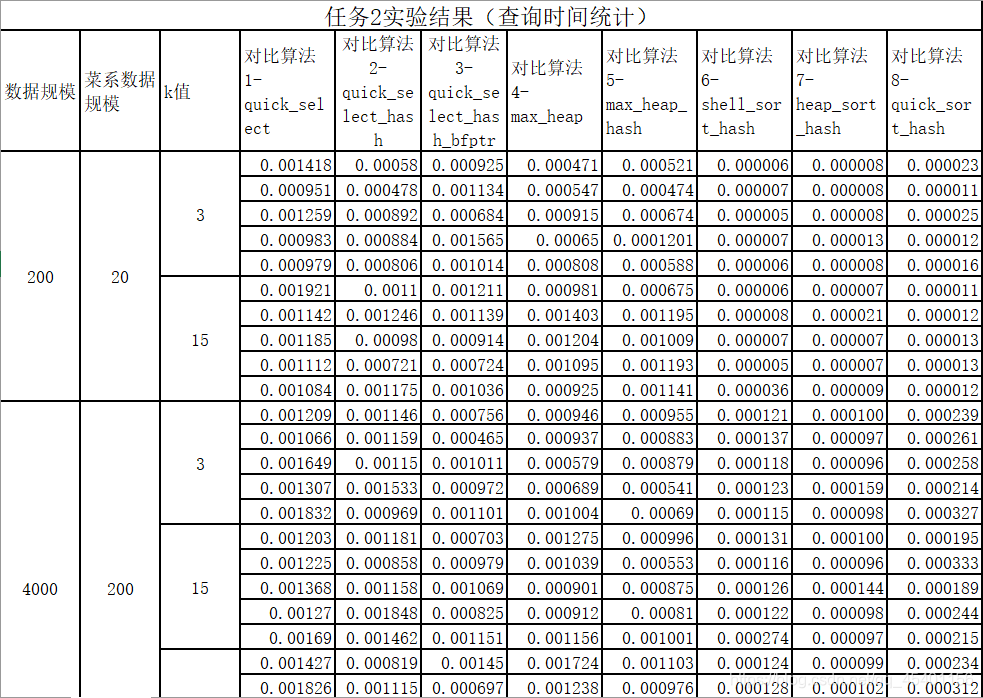
可视化处理:
- 在相同的数据规模 N,相同的菜系规模 T 下,考虑不同 k 值对查找时间的影响,取数据 规模 N=800000,菜系规模 T=80000。
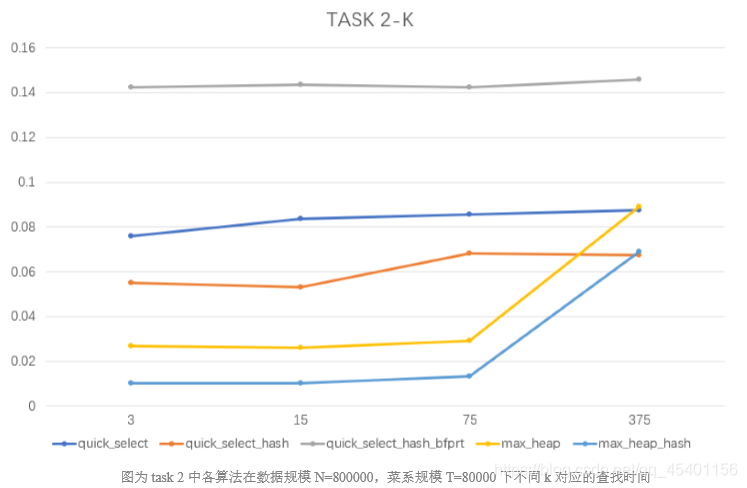
-
Quick_select:只考虑所寻找的目标所在的那一部分子数组,最坏时间复杂度为 O(n^2),平均为 O(n)。且查找时间和轴点(pivot)的选择有关,与 k 值关系不大,所以 折线较为平滑。
(a) 使用了 hash 思维来存储,可以减少需要遍历的元素数量 n,显著提高效率。
(b) 使用 bfprt 可以使轴点选择更居中,但是由于需要选择中值,需要对原数据进行筛 选出同菜系的数据,在数据量较大的情况下,效果很差。 -
Max_heap:时间复杂度为 O(n*lg(k)),曲线斜率变化符合 k 的变化,且利用 hash 思维 来存储,可以减少需要遍历的元素数量 n,显著提高效率。
- 在相同的数据规模 N,相同的 k 值下,考虑不同菜系下规模 T 对查找时间的影响,取数 据规模 N=800000,k=15
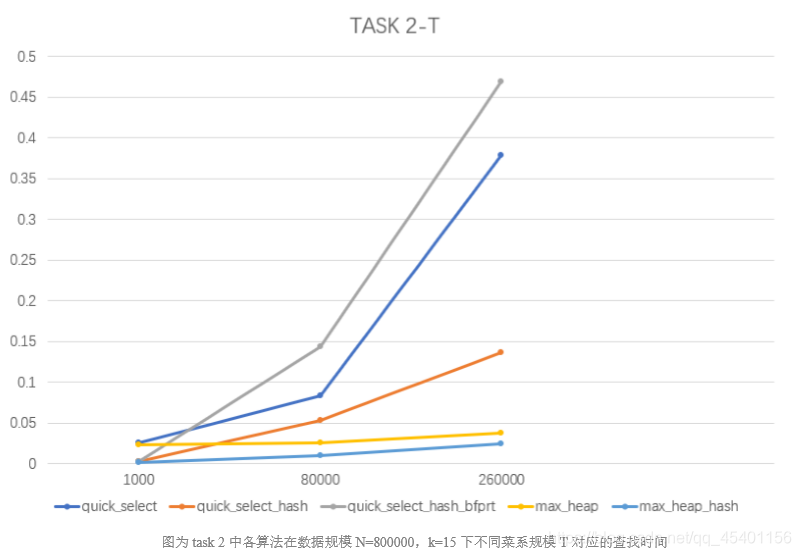
-
采用 hash 来存储数据:由于使用的 hash 函数具有很高的命中率,两个不同菜系的参 观信息存放在一个 vector 数组里的概率非常小,所以算法需要操作的元素规模几乎等 同于菜系下的数据规模 T,少数发生冲突的为 2*T,命中率的高低和 hash_size 的选择 以及 hash 函数有关。
-
Quick_select 算法由于菜系规模的急剧增大,需要调换和比较的次数也急剧增大,增长幅度近似于菜系规模 T 的增长幅度。Quick_selec_hash_bfprt 由于采用线性查找来筛 选同菜系的餐馆信息,并采用插入排序来获取中位数,在大规模数据下优化效率不好,增长幅度近似于 K 的增长幅度。这也是为什么这两种算法在 EOJ 上过不了最后两个点。而 Quick_select_hash 算法的增长幅度也近似于 K 的涨幅,但是由于需要 hash 的高命中率,需要遍历的元素个数相对 N 小很多,能够在 EOJ 上擦边通过。
- 由于在不同的数据规模 N 下菜系下规模 T 差别都很大,以 N 作为变量无法确认单一变 量,不便于分析,下图仅作为输出时间趋势参考,不做具体分析。
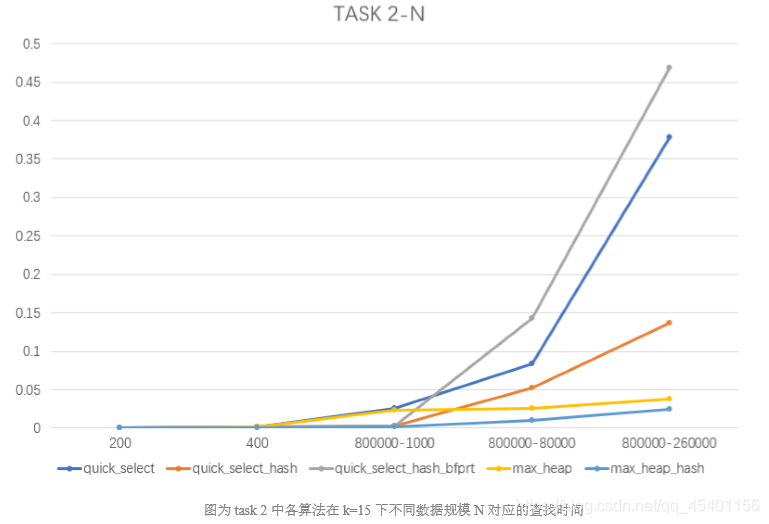
- 在本题实际使用中,Max_heap 的效率是要优于 Quick_select 的,猜测是因为在使用 Quick_select 的时候进行了大量的元素筛选、比较和转移操作,之后还要再做排序,这些 环节耗费了大量的时间,导致其实际使用效率不如 Max_heap。
- 分析在小规模数据下采用了 bfprt 算法获取轴点的方法的特点
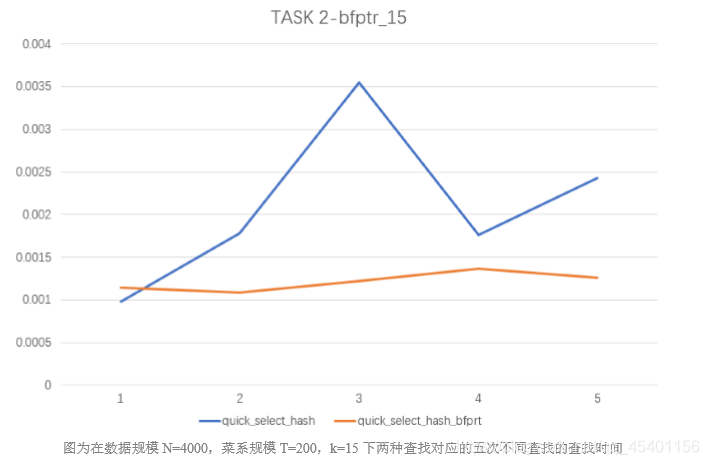
- 从图中折线变化趋势可知,任意查找轴点的 Quick_select 算法的稳定性不好,查找效 率很大程度上取决于轴点的大小,因此曲线波动大。而采用了 bfptr 算法查找的轴点更接 近于数组中值,因此在同等规模下进行查找操作的时候更加稳定,曲线波动小。
- 采用了 bfptr 算法查找的轴点更接近中值,进行二分操作的时候更加接近最优情况, 在数据规模小的情况下,筛选和选中值耗时少,优化效果更明显,查找所用时间更少。
小结
- 菜还是菜,花了一个礼拜整的这个大作业,但是最后ac还是很爽的。最大的感想就是只要坚持不懈地提交,总能够 ac。
- 上数据结构课对我而言最大的快乐就是可以用自己学到的知识来解决一些实际问题。像 之前的回溯法走迷宫,下五子棋,和这次的查找餐厅。
参考资料
-
求 TOPK 的三种方法及分析: https://blog.csdn.net/coder_panyy/article/details/76359368
-
BFPRT 算法(TOP-K 问题): https://ethsonliu.com/2018/03/bfprt.html
-
[数据结构]九大基础排序算法总结: https://blog.csdn.net/yuchenchenyi/article/details/51470500
-
bfptr算法(即中位数的中位数算法):https://blog.csdn.net/a3192048/article/details/82055183
-
《数据结构与程序设计 C++语言描述》,Robert L. Kruse、Alexander J. Ryba 著,钱丽萍 译
补充
经老师讲解、大佬分享,非常优秀的做法应该是k近邻算法或者最邻近搜索。但是因为我很菜,没有了解过,仅在此做个记录,希望之后去了解过再细说。