原题链接
https://www.dotcpp.com/oj/problem3162.html
想直接看题解的,跳转到第三次尝试即可。
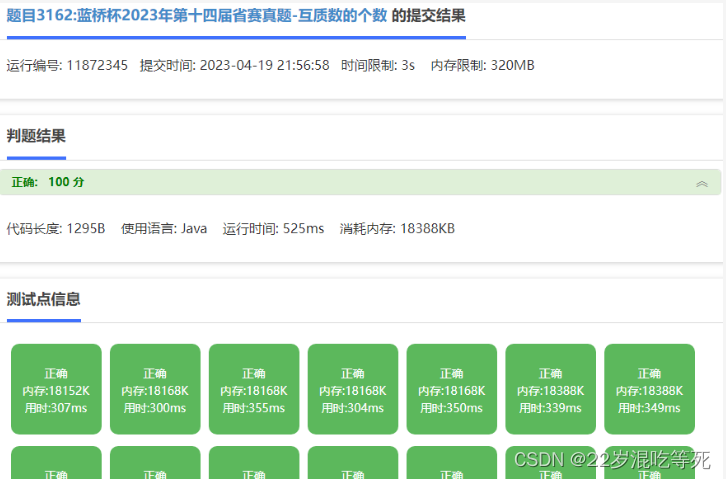
已AC。
解析:
(1)首先大家要知道什么叫互质:
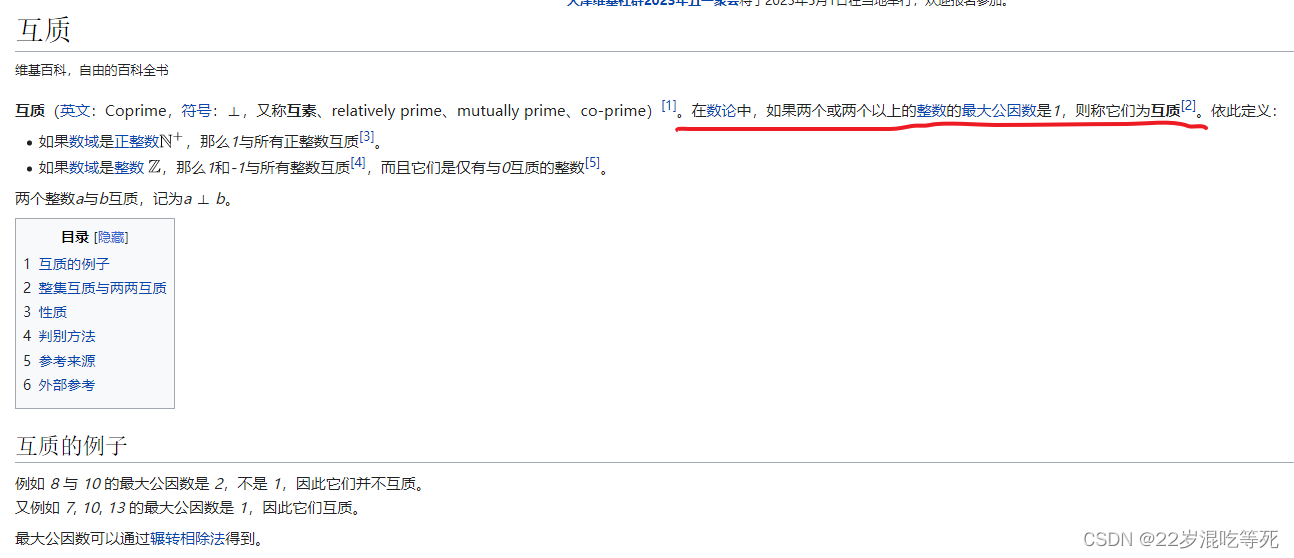
以及它们的性质:

欧拉函数
在数论中,对正整数n,欧拉函数φ(n)是小于或等于n的正整数中与n互质的数的数目。此函数以其首名研究者欧拉命名,它又称为φ函数(由高斯所命名)或是欧拉总计函数(totient function,由西尔维斯特所命名)。
例如φ(8) = 4,因为1,3,5,7均和8互质。
也可以从简化剩余系的角度来解释,简化剩余系(reduced residue system)也称既约剩余系或缩系,是m的完全剩余系中与m互素的数构成的子集,如果模m的一个剩余类里所有数都与m互素,就把它叫做与模m互素的剩余类。在与模m互素的全体剩余类中,从每一个类中各任取一个数作为代表组成的集合,叫做模m的一个简化剩余系。
(1,3,5,7)就构成了8的一个简化剩余系。
参考链接: https://zhuanlan.zhihu.com/p/151756874
第一次尝试代码:
package Dotcpp;import java.io.*;
import java.util.Scanner;public class 题目3180蓝桥杯2023年第十四届省赛真题_互质数的个数 {private static long mod = 998244353L;private static long a,b,ans;static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static StreamTokenizer st = new StreamTokenizer(br);static int nextLong() throws Exception {st.nextToken();return (int) st.nval;}static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));public static void main(String[] args) throws Exception {//Scanner scanner = new Scanner(System.in);a = nextLong();b = nextLong();long n = Euler_pow(a,b-1);long m = Euler(a);System.out.println((n*m%mod)%mod);}private static long Euler(long n) {long res = n;for (long i = 2; i * i <= n; ++i) {if (n % i == 0) {res = res / i * (i - 1);while (n % i == 0) {n /= i;}}}if (n > 1) {res -= res / n;}return res;}private static long Euler_pow(long a, long b) {long ans = 1;while (b != 0){if (b % 2 ==1){ans*=(a%mod)%mod;}a*=a%mod;a=a%mod;b /= 2;}return ans;}
}运行结果:
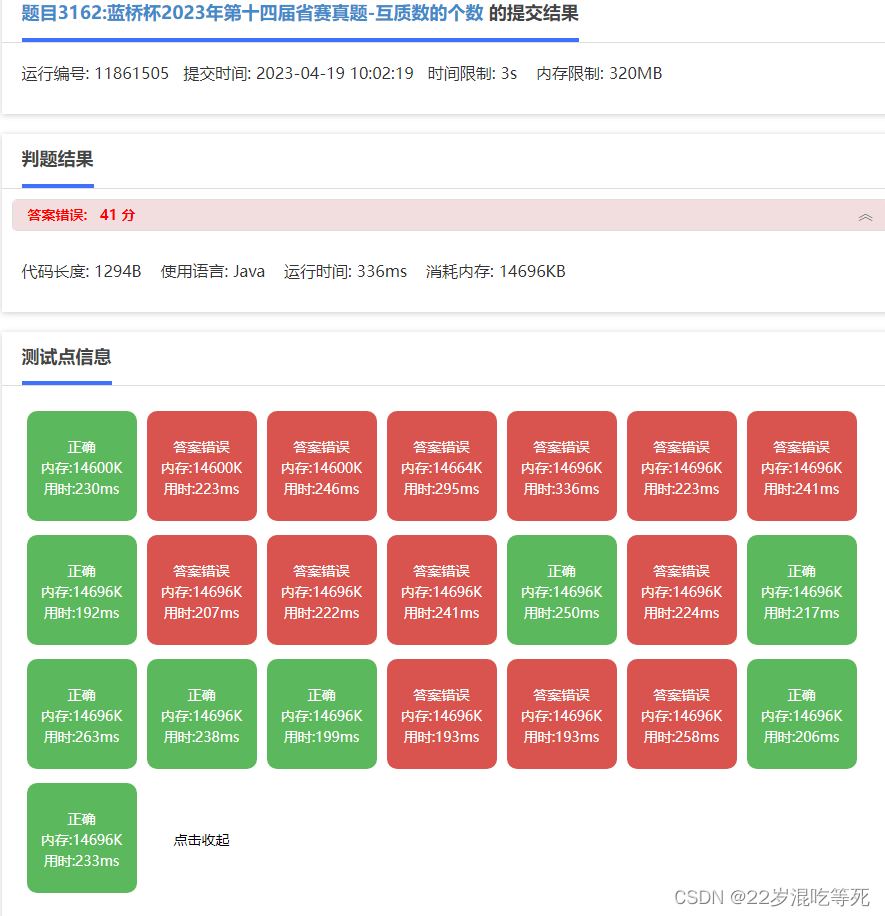
分析:
第二次尝试代码:
package Dotcpp;import java.util.Scanner;public class 题目3180蓝桥杯2023年第十四届省赛真题_互质数的个数__运行错误32分 {private static long mod = 998244353L;private static long a, b, res;public static void main(String[] args) {Scanner scanner = new Scanner(System.in);a = scanner.nextInt();b = scanner.nextInt();long n = Euler_pow(a, b);res = n;for (int i = 2; i <= n / i; i++) {if (n % i == 0) {while (n % i == 0) {n /= i;n%=mod;}res = (res - res / i);res%=mod;}}if (n > 1) {res = (res - res / n);res%=mod;}System.out.println(res%=mod);}private static long Euler_pow(long a, long b) {long ans = 1;while (b > 0) {if ((b & 1) > 0) {ans = ((ans % mod) * (a % mod)) % mod;}a = ((a % mod) * (a % mod)) % mod;b /= 2;}return ans;}}运行结果:
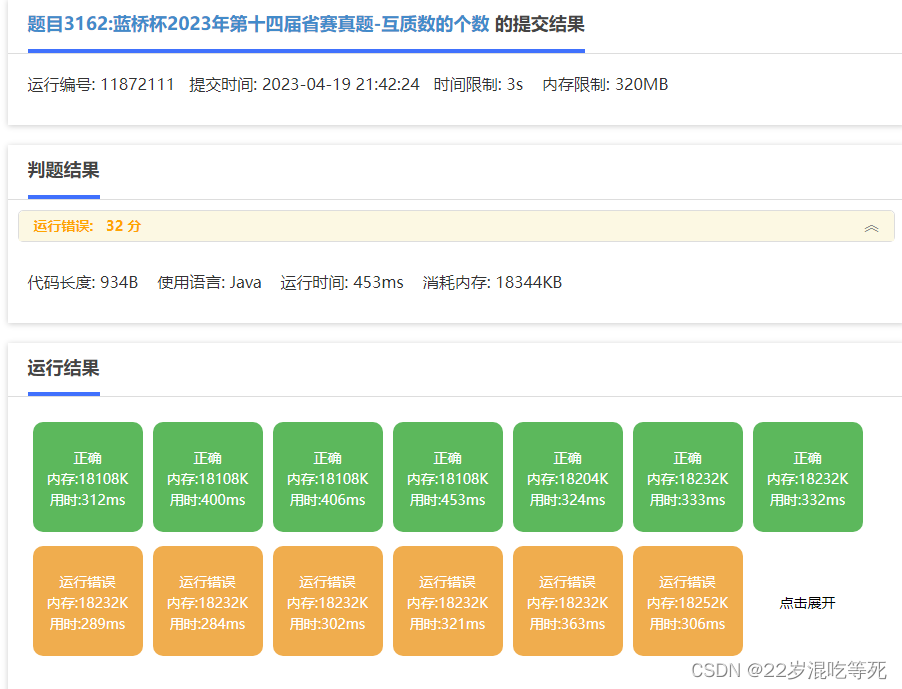
补充说明:
这第二次是我参考其他语言的代码,转化成Java来实现的。
如图可见:
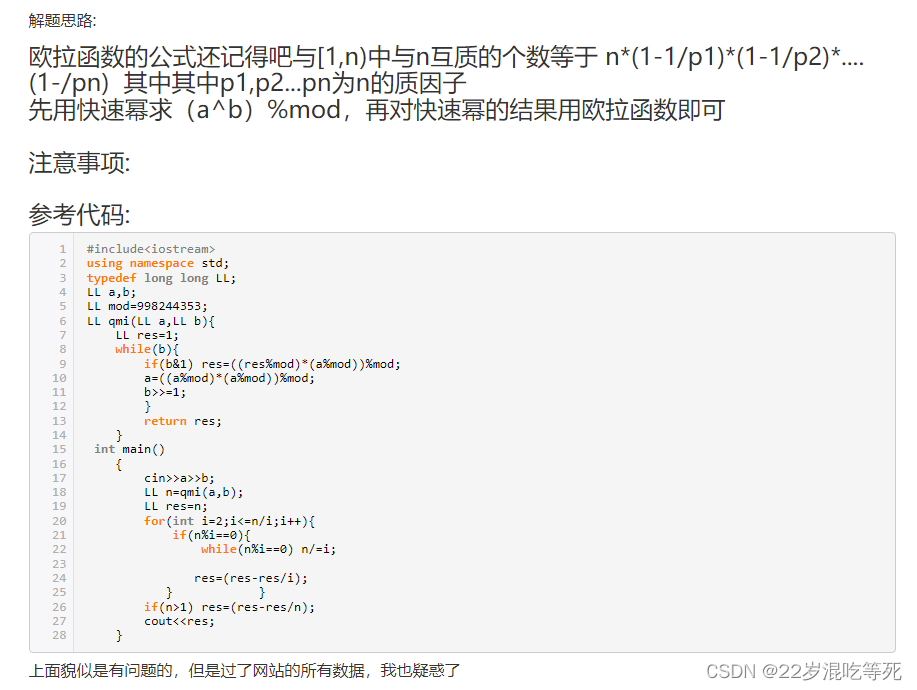
感谢大佬提供的思路: https://blog.dotcpp.com/a/95823
分析:
当时一想,一种方法超时,一种方法会导致报错,两者结合一起,是不是可行呢。?
第三次尝试:
package Dotcpp;import java.io.*;
import java.util.Scanner;public class 题目3180蓝桥杯2023年第十四届省赛真题_互质数的个数 {private static long mod = 998244353L;private static long a,b,res;public static void main(String[] args) throws Exception {Scanner scanner = new Scanner(System.in);a = scanner.nextLong();b = scanner.nextLong();long n = Euler_pow(a,b);res = n;for (int i = 2; i <= n / i; i++) {if (n % i == 0) {while (n % i == 0) {n /= i;n%=mod;}res = (res - res / i);res%=mod;}}if (n > 1) {res = (res - res / n);res%=mod;}scanner.close();System.out.println(res%=mod);}private static long Euler(long n) {long res = n;for (long i = 2; i * i <= n; ++i) {if (n % i == 0) {res = res / i * (i - 1);while (n % i == 0) {n /= i;}}}if (n > 1) {res -= res / n;}return res;}private static long Euler_pow(long a, long b) {long ans = 1;while (b > 0) {if ((b & 1) > 0) {ans = ((ans % mod) * (a % mod)) % mod;}a = ((a % mod) * (a % mod)) % mod;b /= 2;}return ans;}
}结果: