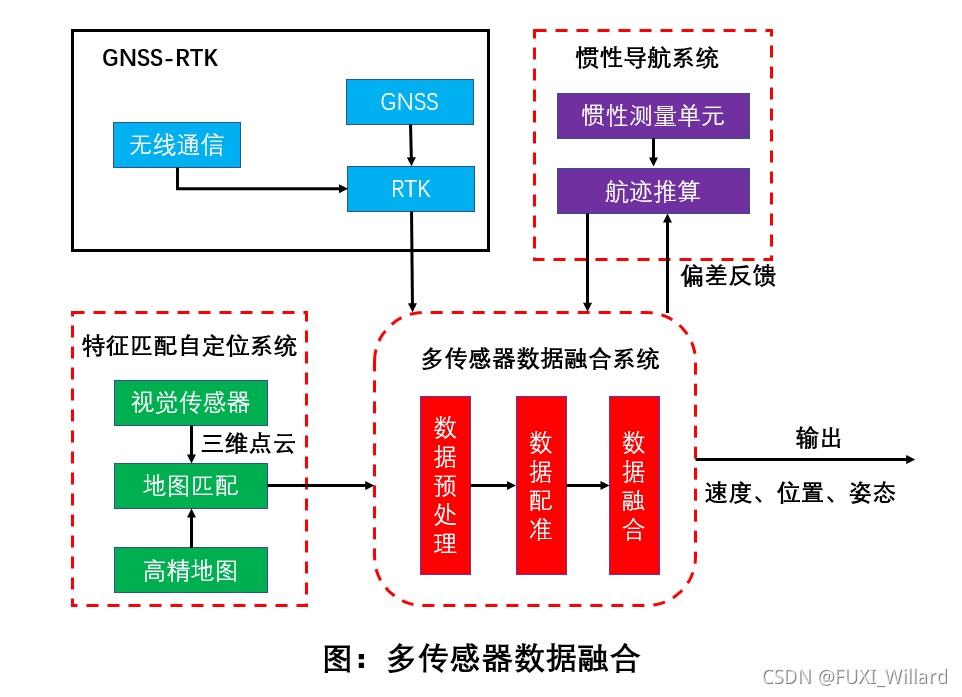
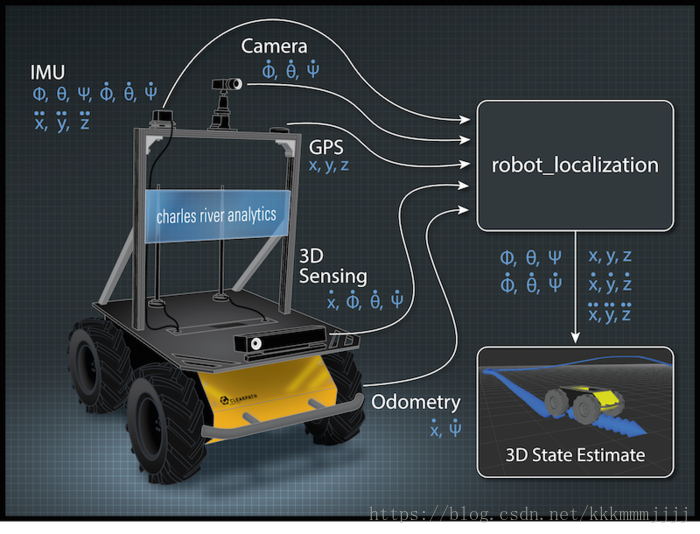
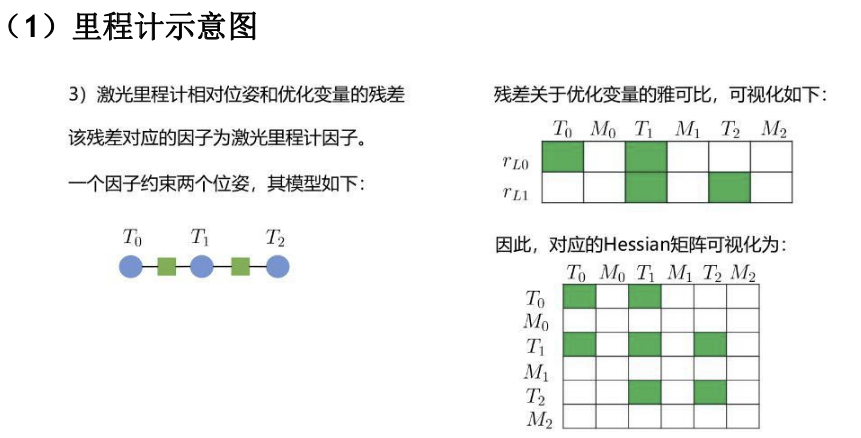
多传感器融合定位十五-多传感器时空标定
- 1. 多传感器标定简介
- 1.1 标定内容及方法
- 1.2 讲解思路
- 2. 内参标定
- 2.1 雷达内参标定
- 2.2 IMU内参标定
- 2.3 编码器内参标定
- 2.4 相机内参标定
- 3. 外参标定
- 3.1 雷达和相机外参标定
- 3.2 多雷达外参标定
- 3.3 手眼标定
- 3.4 融合中标定
- 3.5 总结
- 4. 时间标定
- 4.1 离散时间
- 4.2 连续时间
- 4.3 总结
Reference:
- 深蓝学院-多传感器融合
- 多传感器融合定位理论基础
文章跳转:
- 多传感器融合定位一-3D激光里程计其一:ICP
- 多传感器融合定位二-3D激光里程计其二:NDT
- 多传感器融合定位三-3D激光里程计其三:点云畸变补偿
- 多传感器融合定位四-3D激光里程计其四:点云线面特征提取
- 多传感器融合定位五-点云地图构建及定位
- 多传感器融合定位六-惯性导航原理及误差分析
- 多传感器融合定位七-惯性导航解算及误差分析其一
- 多传感器融合定位八-惯性导航解算及误差分析其二
- 多传感器融合定位九-基于滤波的融合方法Ⅰ其一
- 多传感器融合定位十-基于滤波的融合方法Ⅰ其二
- 多传感器融合定位十一-基于滤波的融合方法Ⅱ
- 多传感器融合定位十二-基于图优化的建图方法其一
- 多传感器融合定位十三-基于图优化的建图方法其二
- 多传感器融合定位十四-基于图优化的定位方法
- 多传感器融合定位十五-多传感器时空标定(综述)
1. 多传感器标定简介
1.1 标定内容及方法

1.2 讲解思路
- 以思路讲解为主,并给出参考文献和开源代码,不做过多细节展开;
- 对已有方法做汇总分析,以求能在新的任务中掌握标定方案设计思路。
2. 内参标定
2.1 雷达内参标定

-
目的
由于安装原因,线束之间的夹角和设计不一致,会导致测量不准。 -
方法
多线束打在平面上,利用共面约束,求解夹角误差。 -
参考
论文:Calibration of a rotating multi-beam Lidar
论文:Improving the Intrinsic Calibration of a Velodyne LiDAR Sensor
论文:3D LIDAR–camera intrinsic and extrinsic calibration: Identifiability and analytical least-squares-based initialization
2.2 IMU内参标定
-
目的
由于加工原因,产生零偏、标度因数误差、安装误差。 -
方法
分立级标定:基于转台;
迭代优化标定:不需要转台。 -
参考
论文:A Robust and Easy to Implement Method for IMU Calibration without External Equipments
代码:https://github.com/Kyle-ak/imu_tk
2.3 编码器内参标定
-
目的
用编码器输出解算车的位移增量和角度增量,需已知轮子半径和两轮轴距。 -
方法
以车中心雷达/组合导航做观测,以此为真值,反推模型参数。 -
参考
论文:Simultaneous Calibration of Odometry and Sensor Parameters for Mobile Robots
2.4 相机内参标定

-
目的
相机与真实空间建立关联,需已知其内参。 -
方法
张正友经典方法
3. 外参标定
3.1 雷达和相机外参标定

-
目的
解算雷达和相机之间的相对旋转和平移。 -
方法
PnP是主流,视觉提取特征点,雷达提取边缘,建立几何约束。 -
参考
论文: LiDAR-Camera Calibration using 3D-3D Point correspondences
代码: https://github.com/ankitdhall/lidar_camera_calibration
论文: Automatic Extrinsic Calibration for Lidar-Stereo Vehicle Sensor Setups
代码: https://github.com/beltransen/velo2cam_calibration
3.2 多雷达外参标定

-
目的
多雷达是常见方案,使用时将点云直接拼接,但前提是已知雷达之间的外参(相对旋转和平移)。 -
方法
基于特征(共面)建立几何约束,从而优化外参。 -
参考
论文:A Novel Dual-Lidar Calibration Algorithm Using Planar Surfaces
代码:https://github.com/ram-lab/lidar_appearance_calibration
3.3 手眼标定

-
目的
手眼标定适用于所有无共视,但是能输出位姿的传感器之间标定。包括:
• 无共视的相机、雷达,或雷达与雷达之间;
• 相机与IMU,或雷达与IMU之间(前提是IMU要足够好,或直接使用组合导航)。 -
方法
均基于公式 A X = X B AX=XB AX=XB -
参考
论文:LiDAR and Camera Calibration using Motion Estimated by Sensor Fusion Odometry
代码:https://github.com/ethz-asl/lidar_align
3.4 融合中标定
-
目的
• 脱离标靶,实现在线标定;
• 某些器件无法提供准确位姿(如低精度IMU),不能手眼标定。 -
方法
在融合模型中,增加外参作为待估参数。 -
参考
众多vio/lio系统,如vins、 lio-mapping、 M-Loam 等
3.5 总结
-
这些方法中,推荐优先级从高到低为:
a. 基于共视的标定
b. 融合中标定
c. 手眼标定 -
建议
应在良好环境下标定,尽量避免不分场景的在线标定。良好环境指观测数据优良的场景,例如:
a. GNSS 信号良好;
b. 点云面特征丰富,没有特征退化;
c. 动态物体较少
4. 时间标定
4.1 离散时间
-
目的
在原有离散时间融合模式下,简单地解决时间同步问题。

-
方案 I
 简单但巧妙的策略: IMU时间保持不变,图像上特征点基于匀速运动模型修改位置。
简单但巧妙的策略: IMU时间保持不变,图像上特征点基于匀速运动模型修改位置。
与不考虑时间误差时相比,架构不变,使用极小的改动,实现了期望的效果。
e l k = z l k − π ( R c k w T ( P l − p c k w ) ) z l k = [ u l k v l k ] T . ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ e l k = z l k ( t d ) − π ( R c k w T ( P l − p c k w ) ) z l k ( t d ) = [ u l k v l k ] T + t d V l k . \begin{array}{l} \mathbf{e}_l^k=\mathbf{z}_l^k-\pi\left(\mathbf{R}_{c_k}^{w^T}\left(\mathbf{P}_l-\mathbf{p}_{c_k}^w\right)\right) \\ \mathbf{z}_l^k=\left[\begin{array}{ll} u_l^k & v_l^k \end{array}\right]^T . \\ \downarrow\downarrow\downarrow\downarrow\downarrow\downarrow\downarrow\downarrow\downarrow\downarrow\downarrow\downarrow\downarrow\downarrow\downarrow \\ \mathbf{e}_l^k=\mathbf{z}_l^k\left(t_d\right)-\pi\left(\mathbf{R}_{c_k}^{w^T}\left(\mathbf{P}_l-\mathbf{p}_{c_k}^w\right)\right) \\ \mathbf{z}_l^k\left(t_d\right)=\left[\begin{array}{ll} u_l^k & v_l^k \end{array}\right]^T+t_d \mathbf{V}_l^k . \end{array} elk=zlk−π(RckwT(Pl−pckw))zlk=[ulkvlk]T.↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓elk=zlk(td)−π(RckwT(Pl−pckw))zlk(td)=[ulkvlk]T+tdVlk.参考文献:Online Temporal Calibration for Monocular Visual-Inertial Systems -
方案 II
在滤波中计算相机位姿时,直接按时间差对积分区间进行调整。
状态量: x = [ x I T I C q ‾ T C p I T t d c 1 T ⋯ c M T ] T \mathbf{x}=\left[\begin{array}{lllllll} \mathbf{x}_I^T & { }_I^C \overline{\mathbf{q}}^T & { }^C \mathbf{p}_I^T & t_d & \mathbf{c}_1^T & \cdots & \mathbf{c}_M^T \end{array}\right]^T x=[xITICqTCpITtdc1T⋯cMT]T
相机位姿估计: c ^ n e w = [ G C q ( t + t d ) ^ G p C ( t + t d ) ^ ] = [ I C q ^ ⊗ G I q ^ ( t + t ^ d ) G p ^ I ( t + t ^ d ) + G I R ^ ( t + t ^ d ) T I p ^ C ] \hat{\mathbf{c}}_{n e w}=\left[\begin{array}{c}{ }_G^C \widehat{\mathbf{q}\left(t+t_d\right)} \\ { }^G \widehat{\mathbf{p}_C\left(t+t_d\right)}\end{array}\right]=\left[\begin{array}{c}{ }_I^C \hat{\mathbf{q}} \otimes{ }_G^I \hat{\mathbf{q}}\left(t+\hat{t}_d\right) \\ { }^G \hat{\mathbf{p}}_I\left(t+\hat{t}_d\right)+{ }_G^I \hat{\mathbf{R}}\left(t+\hat{t}_d\right)^T{ }^I \hat{\mathbf{p}}_C\end{array}\right] c^new=[GCq(t+td) GpC(t+td) ]=[ICq^⊗GIq^(t+t^d)Gp^I(t+t^d)+GIR^(t+t^d)TIp^C]
参考文献:Online Temporal Calibration for Camera-IMU Systems: Theory and Algorithms
4.2 连续时间
- 原因
预积分中把时间差作为待估状态量,对时间差进行建模,如下:
Δ p m i = ∑ k = κ i − 1 ( Δ v m k Δ t k + Δ R m k 2 f ( t k − δ t m − b f m ) Δ t k 2 ) Δ v m i = ∑ k = κ i − 1 Δ R m k f ( t k − δ t m ) − b f m ) Δ t k Δ R m i = ∏ k = κ i = 1 Exp ( ω ( t k − δ t m ) − b ω m ) Δ t k ) , \begin{array}{l} \Delta \mathbf{p}_m^i=\sum_{k=\kappa}^{i-1}\left(\Delta \mathbf{v}_m^k \Delta t_k+\frac{\Delta \mathbf{R}_m^k}{2} \operatorname{f}\left(t_k-\delta_t^m-\mathbf{b}_f^m\right) \Delta t_k^2\right) \\ \left.\Delta \mathbf{v}_m^i=\sum_{k=\kappa}^{i-1} \Delta \mathbf{R}_m^k \mathbf{f}\left(t_k-\delta_t^m\right)-\mathbf{b}_f^m\right) \Delta t_k \\ \left.\Delta \mathbf{R}_m^i=\prod_{k=\kappa}^{i=1} \operatorname{Exp}\left(\omega\left(t_k-\delta_t^m\right)-\mathbf{b}_\omega^m\right) \Delta t_k\right), \end{array} Δpmi=∑k=κi−1(ΔvmkΔtk+2ΔRmkf(tk−δtm−bfm)Δtk2)Δvmi=∑k=κi−1ΔRmkf(tk−δtm)−bfm)ΔtkΔRmi=∏k=κi=1Exp(ω(tk−δtm)−bωm)Δtk),由于要对时间差求雅可比,因此插值函数必须可导,雅可比如下:
Δ R m ( b ω , δ t ) i ≈ Δ R m ( b ˉ ω m , δ ˉ δ m ) i Exp ( ∂ Δ R m i ∂ b ω b ^ ω m + ∂ Δ R m i ∂ δ t δ ^ t m ) . Δ v m ( b f , b ω , δ t ) i ≈ Δ Δ v m ( b ˉ f m , b ˉ m m , δ ˉ t m ) i + ∂ Δ v m i ∂ b f b ^ f m + ∂ Δ v m i ∂ b ω b ^ ω m + ∂ Δ v m i ∂ δ t δ ^ t m Δ p m ( b f , b ω , , δ t ) i ≈ Δ p m ( b f m ‾ , b ˉ m m , δ ˉ t m ) i + ∂ Δ p m m ∂ b f b ^ f m + ∂ Δ p m i ∂ b ω b ^ ω m + ∂ Δ p m i ∂ δ t δ ^ t m \begin{array}{l} \Delta \mathbf{R}_{m\left(\mathbf{b}_\omega, \delta_t\right)}^i \approx \Delta \mathbf{R}_{m\left(\bar{b}_\omega^m, \bar{\delta}_\delta^m\right)}^i \operatorname{Exp}\left(\frac{\partial \Delta \mathbf{R}_m^i}{\partial \mathbf{b}_\omega} \hat{\mathbf{b}}_\omega^m+\frac{\partial \Delta \mathbf{R}_m^i}{\partial \delta_t} \hat{\delta}_t^m\right). \\ \Delta \mathbf{v}_{m\left(\mathbf{b}_f, \mathbf{b}_\omega, \delta_t\right)}^i \approx \Delta \Delta \mathbf{v}_{m\left(\bar{b}_f^m, \bar{b}_m^m, \bar{\delta}_t^m\right)}^i+\frac{\partial \Delta \mathbf{v}_m^i}{\partial \mathbf{b}_f} \hat{\mathbf{b}}_f^m +\frac{\partial \Delta \mathbf{v}_m^i}{\partial \mathbf{b}_\omega} \hat{\mathbf{b}}_\omega^m+\frac{\partial \Delta \mathbf{v}_m^i}{\partial \delta_t} \hat{\delta}_t^m \\ \Delta \mathbf{p}_{m\left(\mathbf{b}_f, \mathbf{b}_{\omega,}, \delta_t\right)}^i \approx \Delta \mathbf{p}_{m\left(\overline{\mathbf{b}_f^m}, \bar{b}_m^m, \bar{\delta}_t^m\right)}^i+\frac{\partial \Delta \mathbf{p}_m^m}{\partial \mathbf{b}_f} \hat{\mathbf{b}}_f^m +\frac{\partial \Delta \mathbf{p}_m^i}{\partial \mathbf{b}_\omega} \hat{b}_\omega^m+\frac{\partial \Delta \mathbf{p}_m^i}{\partial \delta_t} \hat{\delta}_t^m \\ \end{array} ΔRm(bω,δt)i≈ΔRm(bˉωm,δˉδm)iExp(∂bω∂ΔRmib^ωm+∂δt∂ΔRmiδ^tm).Δvm(bf,bω,δt)i≈ΔΔvm(bˉfm,bˉmm,δˉtm)i+∂bf∂Δvmib^fm+∂bω∂Δvmib^ωm+∂δt∂Δvmiδ^tmΔpm(bf,bω,,δt)i≈Δpm(bfm,bˉmm,δˉtm)i+∂bf∂Δpmmb^fm+∂bω∂Δpmib^ωm+∂δt∂Δpmiδ^tm参考文献:3D Lidar-IMU Calibration based on Upsampled Preintegrated Measurements for Motion Distortion Correction - 方法
把输入建立为连续时间函数,从而可以在任意时间求导。 - 参考
a. kalibr 系列
论文:Continuous-Time Batch Estimation using Temporal Basis Functions
论文:Unified Temporal and Spatial Calibration for Multi-Sensor Systems
论文:Extending kalibr Calibrating the Extrinsics of Multiple IMUs and of Individual Axes
代码:https://github.com/ethz-asl/kalibr
b. 其他
论文:Targetless Calibration of LiDAR-IMU System Based on Continuous-time Batch Estimation
代码:https://github.com/APRIL-ZJU/lidar_IMU_calib
4.3 总结
- 时间差估计,在某些情况下不得已而为之,实际中应尽量创造条件实现硬同步;
- 不得不估计时,也应尽量在良好环境下估计。