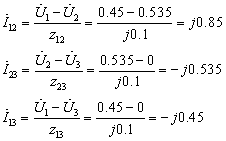计算三相负载功率,下面给出三种方案
一. 通过计算公式
通过大学电路里的计算公式
P=1.732UIcosφ,其中:cosφ:为功率因数,一般取0.85,P:交流电的实际功率,单位:kW,U:交流电的实际电压
需要测量 电压U 电流I 和功率因数 cosφ(如果没有零线,功率因数难以测量)
因此该方法只适合估算
二. 经典的二瓦计法
二瓦计法是一种常用的三相功率测量方法,实践中可以节省一组电流电压测量传感器,节省部分成本,而且不论三相电对称与否,都可以准确测量。
如图所示,这是一个典型的二瓦计法测试原理图,采用两个功率表分别测量A相和C相的电压、电流信号,然后根据基尔霍夫定律分别计算出B相的电压和电流,从而得到三相电压、电流的幅值、相位参数。
基尔霍夫电流定律:电路中任一个节点上,在任一时刻,流入节点的电流之和等于流出节点的电流之和。
基尔霍夫电压定律,任何一个闭合回路中,各元件上的电压降的代数和等于电动势的代数和,即从一点出发绕回路一周回到该点时,各段电压的代数和恒等于零,即∑U=0。
二瓦计法的理论依据是基尔霍夫电流定律,即:在集总电路中,任何时刻,对任意结点,所有流入流出结点的支路电流的代数和恒等于零。也就是说,两根火线的流入电流等于第三根火线的流出电流,或者说,三根火线的电流的矢量和等于零,即:
ia+ib+ic=0 (1)
假设三相负载的中线为N,依据电压的定义:
uab=uan-ubn,ucb=ucn-ubn (2)
三相瞬时功率 p=uan*ia+ubn*ib+ucn*ic (3)
将式(1)和式(2)代入式(3),得:
p=uan*ia+(-ubn*ia+ubn*ia)+ubn*ib+ucn*ic
=uab*ia+ubn(ia+ib)+ucn*ic
=uab*ia+ubn(-ic)+ucn*ic
=uab*ia+ucb*ic
P=P1+P2
有功功率等于瞬时功率在一个周期内求积分再求平均,得到:
P为三相电路有功功率的总和,P1为uab*ia在一个周期内的积分的平均值,P2为ucb*ic在一个周期内的平均值。在正弦稳态电路中:
P=UAB*IA*cosφAB+UCB*IC*cosφCB
P1=UAB*IA*cosφAB
P2=UCB*IC*cosφCB
式中,UAB、IA、UCB、IC均为正弦电压电流的有效值,φAB为UAB和IA的相位差,φCB为UCB和IC的相位差。
从变换的公式中可以看出,采用这种方法进行三相总功率测量时,只需要测量两个电压和两个电流,这就是二瓦计法的推导原理及由来。
二瓦计法测量时,三相电路总功率等于两块功率表的功率之和,每块功率表测量的功率本身无物理意义。
由于二瓦计法的理论依据是基尔霍夫定律,适用于在三相回路中只有三个电流存在的场合
1、三相三线制接法中线不引出(只能采用两瓦计法);
2、 三相三线制接法中线引出但不与地线或试验
在实际应用中,二瓦计法有误区常常被错误认为只适合于三相对称电路的功率测量。根据基尔霍夫定律,并没有要求三相对称,只有ia+ib+ic=0的假设。换句话说,只要满足基尔霍夫定律,测量的精度完全可以满足需求,与是否三相平衡无关。
三. 三相对称电路的简单接法
P = 1.732 * UAC * IB * sinθ
由于是 三相对称电路 UAN ≈ UBN ≈ UCN ≈ UAC / 1.732
IAN ≈ IBN ≈ ICN (此处为有效值,虚拟的中性点N)
且电流和电压的夹角均为 θ
三相瞬时功率 p=Re(uan*ia+ubn*ib+ucn*ic) = Re(3 * ubn * ib) = 3 * UBN * IBN * cosθ = 1.732 * UAC * IB * cosθ
由于uac 与ubn 夹角成90度,p = Im(1.732 * uac * ib ) = 1.732 * UAC * IB *sinθ
在实际应用中,该方法只适合于三相对称电路的功率测量。只需要一个功率计(计无功功率),数值乘以 1.732,及为当前实时功率。
单相电能芯片可以使用该方法计量三相负载的功率,用在精度场合不是很高的地方还是不错的,优点是接线简单,互感器可以不分正反。