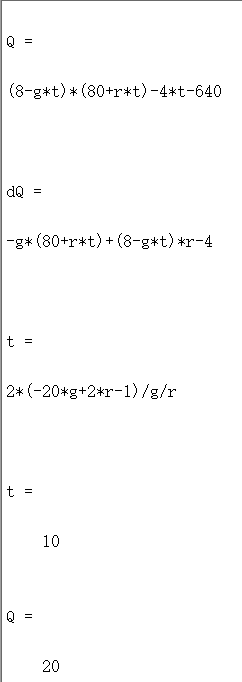一，模型

目标函数（生猪出售纯利润，元）： Q(t)=(8-gt)(80+rt)-4t-640 其中，t≥0 为第几天出售，g 为每天价格降低值（常数，元/公斤），r 为每天生猪体 重增加值（常数，公斤）。 求 t 使 Q(t)最大。

1. 图解法

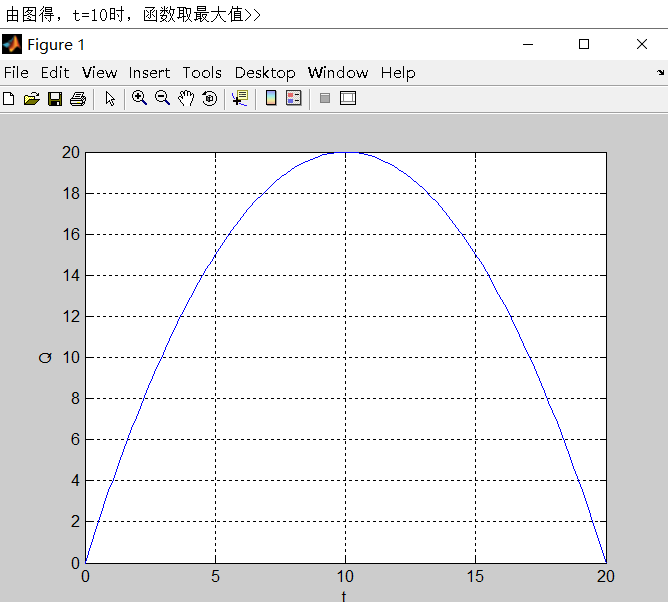
绘制目标函数 Q(t)=(8-gt)(80+rt)-4t-640 的图形（0≤t≤20）。其中， g=0.1, r=2。

clear;clc;
g=0.1;r=2;
fplot(@(t)(8-g*t)*(80+r*t)-4*t-640,[0,20]);
grid;
xlabel('t'); ylabel('Q');
fprintf('由图得，t=10时，函数取最大值');

结果

2. 代数法

对目标函数 Q(t)=(8-gt)(80+rt)-4t-640 用 MATLAB 求 t 使 Q(t)最大。其中，r,g 是待定参数。

clear;clc;
syms t;%定义符号变量 t
Q=sym('(8-g*t)*(80+r*t)-4*t-640') %建立符号表达式
dQ=diff(Q,'t') %求微分 dQ/dt
t=solve(dQ,t) %求 dQ=0 的解 t
r=2;g=0.1;
t=eval(t) %求 r=2,g=0.1 时的 t 值
Q=eval(Q) %求 r=2,g=0.1,t=10 时的 Q 值（最大值）

结果