一、前言
此示例显示了基于约束优化过程的自校准过程。利用机会来源同时估计阵列形状的不确定性和来源方向。此示例需要优化工具箱。
理论上,可以设计一个完美的均匀线性阵列(ULA)来执行各种处理,例如波束成形或到达方向估计。通常,此阵列在部署之前将在受控环境中进行校准。但是,在操作过程中系统中可能会出现不确定性,表明阵列需要重新校准。例如,环境影响可能会导致阵列元素位置受到干扰,从而引入阵列形状的不确定性。这些不确定性的存在会导致阵列处理算法的检测、分辨率和估计性能迅速下降。因此,尽快消除这些阵列不确定性至关重要。
有许多阵列校准算法。本例重点介绍其中的一类,即自校准(也称为自动校准),其中不确定性与未知位置的许多外部源的位置一起估计[1]。与先导校准不同,这允许在鲜为人知的环境中重新校准阵列。然而,一般来说,这会导致少量的信号观测和大量的未知数。有许多方法可以解决此问题,如[2]中所述。一种是针对成本函数进行构建和优化。这些成本函数往往是高度非线性的,并且包含局部最小值。在本例中,基于多重信号分类(MUSIC)算法[3]的成本函数被形成并使用优化工具箱作为fmincon优化问题求解。在文献中,还存在许多其他组合[2]。
二、完美的阵列
首先考虑部署一个以半波长间距运行的 5 元件 ULA。在这样的数组中,可以很容易地计算元素位置。
三、一个不那么完美的阵列
接下来,假设阵列在运行时受到扰动,因此在 x 和 y 维度上经历阵列形状的不确定性。为了固定全局轴,假设第一个传感器和第二个传感器的方向是 [4] 中规定的。
四、可视化阵列缺陷
下图显示了已部署阵列和扰动阵列之间的差异。

五、DOA估计的退化
上一节显示了已部署阵列与在运行时发生扰动的阵列之间的区别。如果盲目地使用为已部署阵列设计的处理,阵列的性能就会降低。例如,考虑使用波束扫描估计器来估计 -3、20 和 40 度方位角处 85 个未知源的方向。
这些不确定性会降低阵列性能。自校准允许使用机会源重新校准阵列,而无需知道其位置。
六、自校准
许多自校准方法基于优化成本函数来联合估计未知阵列和源参数(例如阵列传感器和源位置)。必须仔细选择成本函数和优化算法,以鼓励尽可能轻松快速地达成全局解决方案。此外,必须针对给定方案调整与优化算法关联的参数。文献中存在许多成本函数和优化算法的组合。对于此示例场景,选择音乐成本函数 [3] 以及 fmincon 优化算法。随着场景的变化,根据校准算法的鲁棒性调整所使用的方法可能是合适的。例如,在本例中,随着信号源远离末端火力或阵列元素数量的增加,校准算法的性能会下降。先前估计的源位置的初始估计值用作优化过程的初始化准则。

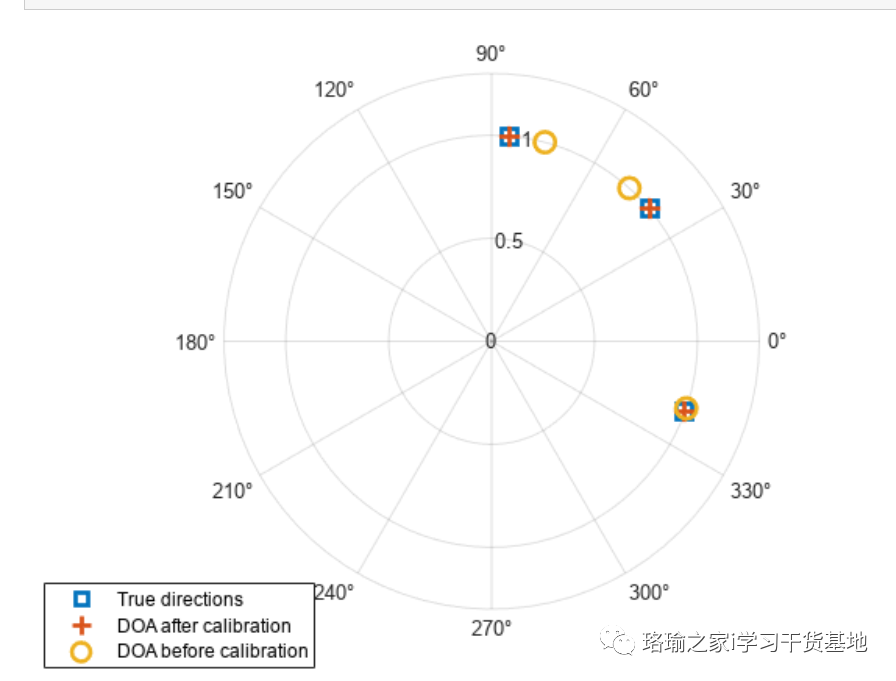
通过执行此校准过程,源估计的准确性已显着提高。此外,还估计了扰动传感器的位置,这些位置将来可以用作新的阵列几何形状。
七、总结
此示例显示了阵列形状的不确定性如何影响估计未知源到达方向的能力。该示例还说明了如何使用自校准来克服这些扰动的影响并同时估计这些不确定性。
八、参考文献
[1]Van Trees, H. Optimum Array Processing. New York: Wiley-Interscience, 2002.
[2] E Tuncer and B Friedlander. Classical and Modern Direction-of-Arrival Estimation. Elsevier, 2009.
[3] Schmidt, R. O. "Multiple Emitter Location and Signal Parameter Estimation." IEEE Transactions on Antennas and Propagation. Vol. AP-34, March, 1986, pp. 276-280.
[4] Y. Rockah and P. M. Schultheiss. Array shape calibration using sources in unknown locations- Part I: Farfield sources. IEEE Trans. ASSP, 35:286-299, 1987.
九、程序
使用Matlab R2022b版本,点击打开。(版本过低,运行该程序可能会报错)
打开下面的“example.mlx”文件,点击运行,就可以看到上述效果。
下载方式一:基于matlab使用自校准来适应阵列不确定性资源-CSDN文库
下载方式二:基于matlab使用自校准来适应阵列不确定性-文库



