1. 背

用graph按照无向图的规则读图，进行按层遍历（bfs），用哈希存储每个节点的层数。
最后遍历connecttions数组，第一个参数必须大于第二个参数，凡是不满足的都记为需要修改的。

2. 题的内容

n 座城市，从 0 到 n-1 编号，其间共有 n-1 条路线。因此，要想在两座不同城市之间旅行只有唯一一条路线可供选择（路线网形成一颗树）。去年，交通运输部决定重新规划路线，以改变交通拥堵的状况。

路线用 connections 表示，其中 connections[i] = [a, b] 表示从城市 a 到 b 的一条有向路线。

今年，城市 0 将会举办一场大型比赛，很多游客都想前往城市 0 。

请你帮助重新规划路线方向，使每个城市都可以访问城市 0 。返回需要变更方向的最小路线数。

题目数据 保证 每个城市在重新规划路线方向后都能到达城市 0 。

示例 1：

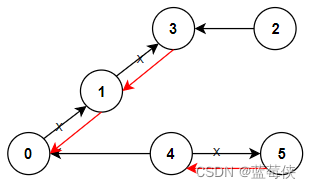
输入：n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
输出：3
解释：更改以红色显示的路线的方向，使每个城市都可以到达城市 0 。
示例 2：

输入：n = 5, connections = [[1,0],[1,2],[3,2],[3,4]]
输出：2
解释：更改以红色显示的路线的方向，使每个城市都可以到达城市 0 。
示例 3：

输入：n = 3, connections = [[1,0],[2,0]]
输出：0

这道题的描述有点问题，第一种情况，其实可以两次就解决，把0-1删掉，把3连到0上就行了。
只能说这题的描述是只能在原有的方向上变向吧。

#include <stdc++.h>using namespace std;class Node {public:int value_;vector<Node*> next_node_;  ///<无向Node(int value) : value_(value) {}
};class Graph {public:unordered_map<int, Node*> node_;Graph(int n, const vector<vector<int>>& graph) {for (int i = 0; i < n; ++i) node_[i] = new Node(i);for (auto vec : graph) {int first = vec[0], end = vec[1];Node* firstNode = node_[first];Node* endNode = node_[end];firstNode->next_node_.push_back(endNode);endNode->next_node_.push_back(firstNode);}}~Graph() {for (auto node_pair : node_) delete (node_pair.second);}private:
};int minReorder(int n, const vector<vector<int>>& connections) {Graph graph(n, connections);unordered_map<int, int> layer;queue<int> bfs;bfs.push(0);layer[0] = 0;int count = 0;while (!bfs.empty()) {queue<int> bfs_tmp;bfs.swap(bfs_tmp);++count;while (!bfs_tmp.empty()) {int cur_node = bfs_tmp.front();bfs_tmp.pop();for (Node* next_node : graph.node_[cur_node]->next_node_) {if (layer.find(next_node->value_) == layer.end()) {layer[next_node->value_] = count;bfs.push(next_node->value_);}}}}int ret = 0;for (auto vec : connections) {int first_layer = layer[vec[0]];int end_layer = layer[vec[1]];if (first_layer < end_layer) ++ret;}return ret;
}int main() {cout << minReorder(3, {{1, 0}, {2, 0}}) << endl;return 0;
}