上个月在网上看到一道数学题，于是写了个算法进行计算，别人和我说这叫蒙特卡罗。

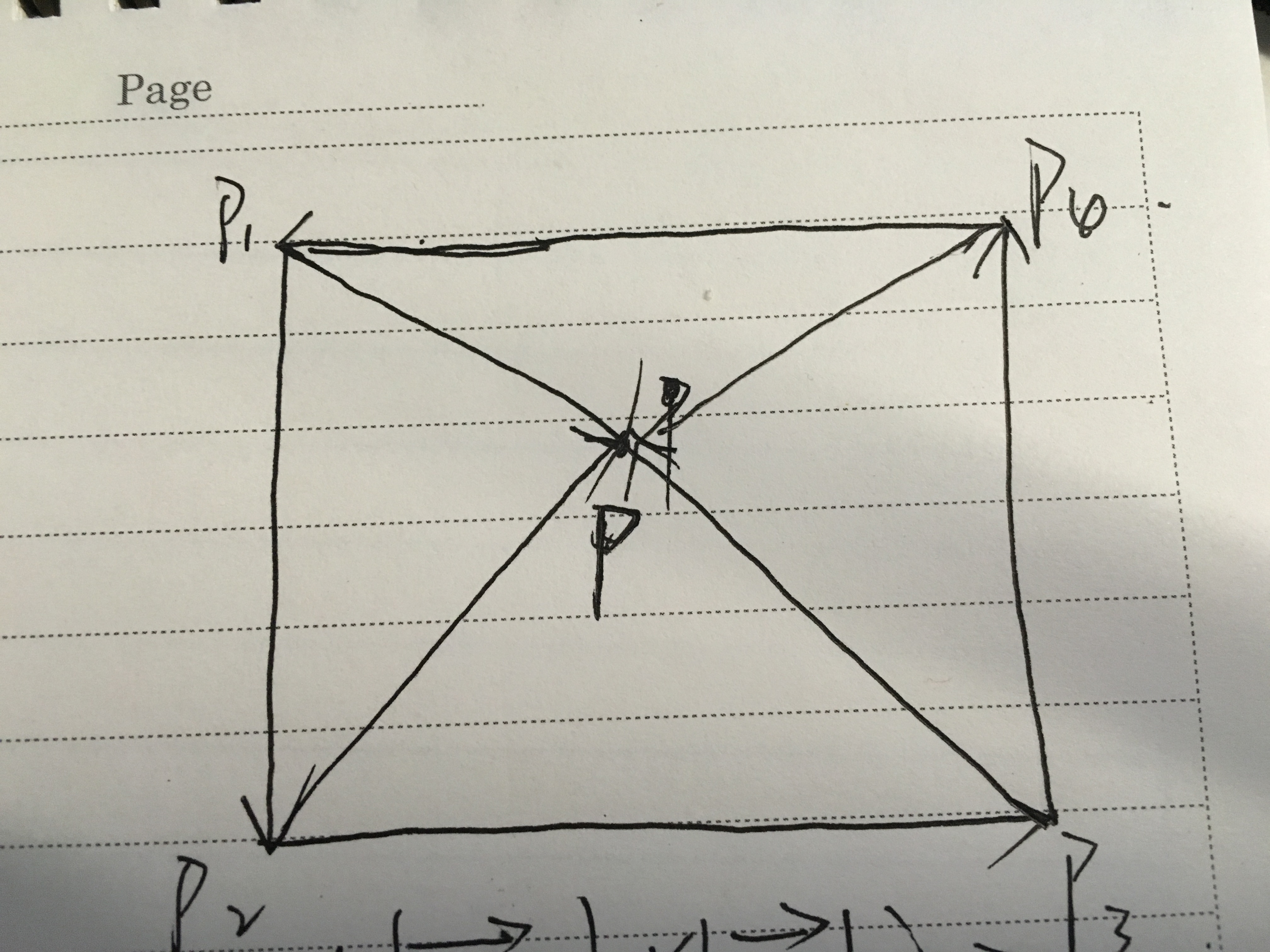
题目如下：

我写的代码如下：

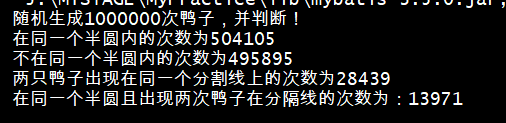
package DuckCircle;import java.util.Random;public class DuckTime {private static int duck1=0;private static int duck2=0;private static int duck3=0;private static int duck4=0;public static Random r=new Random();//有鸭子出现在分隔线上private static int sbDuck=0;//有鸭子出现在分隔线上private static int VIPsbDuck=0;public static void main(String[] args) {int samtimes=0;int notsamtimes=0;int times=1000000;System.out.println("随机生成"+times+"次鸭子，并判断！");for (int i = 0; i <times; i++) {if (judgeDuck())samtimes++;else notsamtimes++;}System.out.println("在同一个半圆内的次数为"+samtimes);System.out.println("不在同一个半圆内的次数为"+notsamtimes);System.out.println("两只鸭子出现在同一个分割线上的次数为"+sbDuck);System.out.println("在同一个半圆且出现两次鸭子在分隔线的次数为："+VIPsbDuck);}//以原点为圆心把每个鸭子的位置写成极坐标// 判断是否在一个半圆内的时候距离不是必要因素// 所以只生成角度public static void getRandomDuck(){duck1=r.nextInt(360)+1;duck2=r.nextInt(360)+1;duck3=r.nextInt(360)+1;duck4=r.nextInt(360)+1;}//根据当前鸭子角坐标获得一个半圆区域public static int[] getHalfCircle(int a){if (a<=180)return new int[]{a,a+180};else return new int[]{a-180,a};}//随机生成一次鸭子并判断是否在一个半圆内public static boolean judgeDuck(){//记录本次开始前的sbduck数量；int Sduck=sbDuck;//随机获取四只鸭子getRandomDuck();//把鸭子放进数组int[] duck={duck1,duck2,duck3,duck4};//遍历每只鸭子for (int i = 0; i < duck.length; i++) {//根据当前鸭子位置获取一个半圆区域，不在该区域内就是另外一个半圆内int[] halfCircle = getHalfCircle(duck[i]);//在该半圆内的鸭子个数int countthis=0;//在另一个半圆内鸭子的个数int countthat=0;//在本次遍历出现在分隔线上的鸭子int thisSBDuck=0;for (int j = 0; j < duck.length; j++) {//去除该鸭子本身if (j==i)continue;//如果该鸭子在对分线上则同时在两个半圆内if (duck[j]==halfCircle[0]||duck[j]==halfCircle[1]){countthis++;countthat++;if (Sduck==sbDuck){sbDuck++;//该参数在一次生成鸭子判断中只能增加一次；}thisSBDuck++;continue;}//判断鸭子是在哪个半圆内if (duck[j]>halfCircle[0]&&duck[j]<halfCircle[1])countthis++;else countthat++;}//不管哪个半圆鸭子数等于3，就返回trueif (countthis==3||countthat==3){if (thisSBDuck!=0)VIPsbDuck++;return true;}}//否则返回falsereturn false;}
}

运行结果如下：