学习目标:
要学习二维随机变量的条件分布,我可能会采取以下步骤:
-
复习边缘分布和联合分布:首先需要了解二维随机变量的边缘分布和联合分布的概念以及相应的公式。
-
复习条件概率:学习条件概率的定义和计算公式,理解条件概率的含义和作用。
-
掌握条件分布的定义:理解条件分布的概念和定义,了解条件分布的性质和特点。
-
学习条件分布的计算方法:学习如何计算条件分布,包括离散型随机变量和连续型随机变量的条件分布。
-
练习例题:通过大量的例题来巩固所学知识,并掌握如何应用条件分布解决实际问题。
-
拓展应用:探究条件分布在其他领域中的应用,如机器学习中的贝叶斯分类器等。
在学习过程中,需要注意以下重点、难点和易错点:
-
熟练掌握边缘分布和联合分布的概念和公式,理解二维随机变量的含义和作用。
-
理解条件概率的概念和计算方法,能够熟练地计算条件概率。
-
了解条件分布的定义和性质,能够判断条件分布的类型并计算其概率密度或概率分布律。
-
注意离散型随机变量和连续型随机变量在条件分布中的区别,掌握它们的计算方法。
-
注意条件分布与边缘分布和联合分布之间的关系,理解它们之间的联系和作用。
-
在解决实际问题时,要注意问题的描述和条件的转换,避免出现计算错误。
-
多做练习,提高对条件分布的理解和应用能力。

我的理解:
离散型随机变量的条件分布指在给定另一随机变量的取值条件下,该随机变量的取值的概率分布。假设 X 和 Y是两个离散型随机变量,P(X=x,Y=y) 是它们的联合概率分布,则在给定 Y=y 的条件下,X的条件概率分布为:
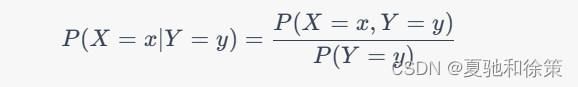
其中,P(Y=y)称为边缘概率分布。类似地,给定 X=x的条件下Y的条件概率分布为:
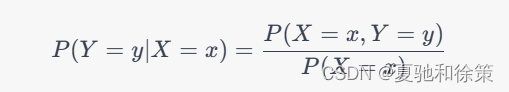
其中,P(X=x)也称为边缘概率分布。
需要注意的是,条件分布只有在 P(Y=y)>0或 P(X=x)>0 的条件下才有定义。



我的理解:
对于连续型二维随机变量 (X,Y),给定条件 Y=y下X的条件分布为:
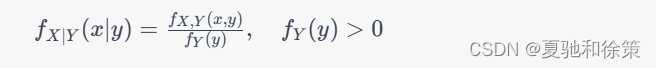
其中 f_{X,Y}(x,y)为 (X,Y)的联合概率密度函数,f_Y(y)为 Y的概率密度函数。
类似地,给定条件 X=x 下 Y 的条件分布为:
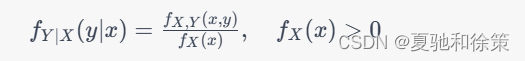
其中 f_X(x)为X的概率密度函数。
在实际应用中,我们常常需要求解一些与条件分布相关的问题,例如求解条件期望、条件方差、条件概率等等。对于这些问题,我们可以根据条件分布的定义,将其转化为单变量随机变量的问题来求解。
总结:
二维随机变量的条件分布是概率论中的重要概念之一。其重点在于理解条件概率的概念和公式,以及在不同类型的二维随机变量中如何求解条件分布。下面是一些可能的重点、难点和易错点的总结:
重点:
- 理解条件概率的概念和公式:条件概率是指在已知某些条件下,另一事件发生的概率。它的公式是 P(A|B) = P(A∩B) / P(B),其中 A∩B 表示事件 A 和事件 B 的交集。
- 理解条件分布的概念:条件分布是指在已知某些条件下,另一随机变量的分布。它的公式是 P(Y=y|X=x) = P(X=x,Y=y) / P(X=x),其中 X 和 Y 是两个随机变量。
- 熟练掌握边缘分布和联合分布的概念和计算方法:边缘分布是指一个随机变量的概率分布,而联合分布是指多个随机变量的概率分布。在求解条件分布时,需要用到这些概念和计算方法。
难点:
- 确定条件分布的类型:在不同的二维随机变量中,条件分布的类型有所不同,比如连续型二维随机变量的条件分布通常是概率密度函数,而离散型二维随机变量的条件分布通常是概率分布律。因此,需要针对不同类型的随机变量进行分类讨论。
- 掌握条件分布的计算方法:在求解条件分布时,需要根据条件概率的公式和边缘分布、联合分布的计算方法,确定条件分布的公式或计算步骤。这通常需要一定的数学技巧和思维灵活性。
- 确定条件变量的范围:在求解条件分布时,需要确定条件变量的取值范围,以便进行条件概率和条件分布的计算。如果条件变量的取值范围不确定或计算错误,可能会导致条件分布的计算错误。
易错点:
- 混淆条件概率和条件分布:有时候容易混淆条件概率和条件分布的概念和计算方法,导致计算错误。
- 忘记考虑条件变量的范围:在求解条件分布时,有时候会忘记考虑条件变量的取值范围,导致条件分布的计算错误。
- 求解边缘分布和联合分布时出错