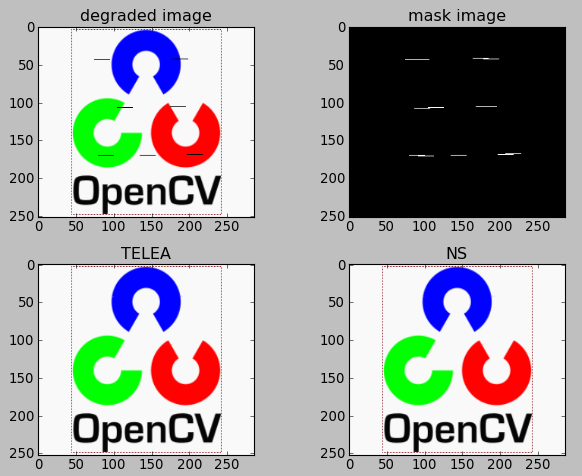
Python-OpenCV中的cv2.inpaint()函数

import numpy as np
import cv2img = cv2.imread('messi_2.jpg') #待修复图像
mask = cv2.imread('mask2.png',0)# 8位1通道掩码图像dst = cv2.inpaint(img,mask,inpaintRadius=6,flags=cv2.INPAINT_NS)
或
dst = cv2.inpaint(img,mask,inpaintRadius=6,flags=cv2.INPAINT_TELEA)cv2.imshow('dst',dst)
cv2.waitKey(0)
cv2.destroyAllWindows()

理论基础

CVPR 2001 Navier-Stokes, Fluid Dynamics, and Image and Video Inpainting

dst = cv2.inpaint（src，mask, inpaintRadius，flags）
- src：输入8位1通道或3通道图像。
- inpaintMask：修复掩码，8位1通道图像。非零像素表示需要修复的区域。
- dst：输出与src具有相同大小和类型的图像。
- inpaintRadius：算法考虑的每个点的圆形邻域的半径。
- flags：INPAINT_NS基于Navier-Stokes的方法Alexandru Telea的INPAINT_TELEA方法

Bertalmio，Marcelo，Andrea L. Bertozzi和Guillermo Sapiro于2001年撰写的“Navier-Stokes，流体动力学和图像和视频修补”一文。该算法基于流体动力学并利用偏微分方程。基本原则是heurisitic。它首先沿着已知区域的边缘行进到未知区域（因为边缘是连续的）。它继续等照片（连接具有相同强度的点的线，就像轮廓连接具有相同高度的点一样），同时在修复区域的边界处匹配渐变矢量。为此，使用来自流体动力学的一些方法。获得颜色后，填充颜色以减少该区域的最小差异。使用标志cv2.INPAINT_NS启用此算法。

图像修复涉及使用周围区域的信息填充部分图像或视频。应用包括修复损坏的照片和电影以及移除选定的对象。本文介绍了一类数字修复的自动化方法。该方法利用经典流体动力学的思想，将等照度线从外部连续传播到待修复区域。其主要思想是将图像强度视为二维不可压缩流的“流函数”。图像强度的拉普拉斯函数起着流体涡度的作用；
它被传输到由流函数定义的向量场来修复的区域。所得到的算法被设计为在匹配修复区域边界处的梯度向量的同时继续等照度图。
该方法直接基于流体动力学的Navier-Stokes方程，具有理论和数值结果成熟的直接优势。这是一种将计算流体力学的思想引入计算机视觉和图像分析问题的新方法。

An ImageInpainting Technique Based On the Fast Marching MethodJanuary( 2004Journal of Graphics Tools)

现在假设p点是我们要修复的像素。以p为中心选取一个小邻域B(ε），该邻域中的点像素值都是已知的（只要已知的）。（这个ε就是opencv函数中参数 inpaintRadius）

一点的恢复公式

q为 Bε（p）中的一点，由q点计算P的灰度值公式如下:
$$I_q(p)=I(q)+\nabla I(q)(p-q)\text{\hspace{1em}(1)}$$

全局的恢复公式需要用w加权

$$I(p)=\frac{{\sum }_{q\in B(\epsilon )}w(p,q)\cdot I_q(p)}{{\sum }_{q\in B(\epsilon )}w(p,q)}\text{\hspace{1em}(2)}$$
其中权重：
$$w(p,q)=dir(p,q)\cdot dst(p,q)\cdot lev(p,q)$$

图像的恢复过程

δΩi = boundary of region to inpaint//修复区域的边缘
δΩ = δΩi
while (δΩ not empty)
{p = pixel of δΩ closest to δΩi//修复距离边缘最近的像素inpaint p using Eqn.2//利用公式2修复p点advance δΩ into Ω//把边缘向里行进
}

FMM论文地址
参考：https://zhuanlan.zhihu.com/p/365677164

参考与更多

OpenCV-Python教程:57.图像修复

Chan T, Shen J. Local inpainting models and TV inpainting
$$I(u)={\iint }_{\Omega }|\nabla u(x,y)|dxdy$$

Ω是待修复区域，目的是求出使这个泛函取得最小值的函数u(x,y,t)
用的是欧拉-拉格朗日方法，求得梯度流为 :

$$\frac{\partial u}{\partial t}=div[\frac{\nabla u}{|\nabla u|}]$$
解释