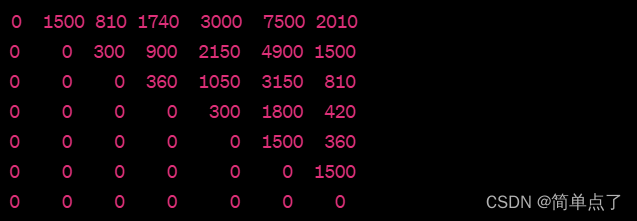
对矩阵规模序列<5,10,3,12,5,50,6>,求矩阵链最优括号化方案
理解符号的含义
n=6
矩阵A1A2A3A4A5A6
本质是找一个最优的子结构
1.重要的递推公式
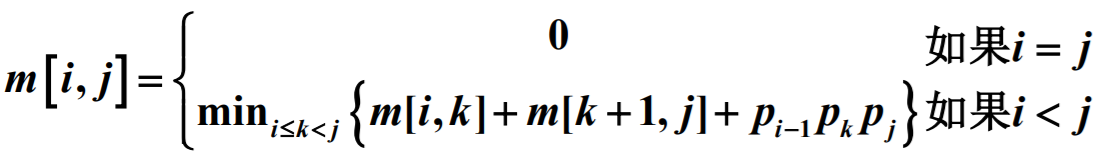
2.关键是求最小的m[i,j]就是乘积次数最少的。
k 的位置只有 j − i 种可能
3.下面是详细的解题的方案
根据矩阵链乘法问题,对于矩阵规模序列<5,10,3,12,5,50,6>,我们需要求出矩阵链的最优括号化方案。下面是求解过程:
首先,我们可以使用动态规划来求解矩阵链的最优括号化方案。定义一个二维数组m和一个二维数组s,其中m[i][j]表示将Ai到Aj这段矩阵链相乘所需的最少乘法次数,s[i][j]表示将Ai到Aj这段矩阵链进行括号化的最优方案中,第一次进行乘法运算的位置。
对于矩阵规模序列<5,10,3,12,5,50,6>,我们可以按照矩阵链乘法问题的动态规划思路,采用自底向上的方式进行求解。具体过程如下:
- 初始化m[i][i]=0,表示单个矩阵相乘的乘法次数为0。
- 对于每个区间长度len,从长度为2的区间开始,一直计算到长度为n的区间。在计算每个长度为len的区间时,需要计算出所有可能的括号化方案,并选择其中的最优方案。
- 对于长度为len的区间[i,j],枚举其内部的分割点k,将其拆分成两个子问题:[i,k]和[k+1,j]。计算出将这两个子问题相乘所需的最小乘法次数,然后将它们相加,加上将它们相乘的乘法次数,即可得到将区间[i,j]括号化的最小乘法次数。
- 在计算出所有可能的括号化方案之后,选择其中的最优方案,并将对应的括号化位置记录在s[i][j]中。
- 最终,m[1][n]即为整个矩阵链的最小乘法次数,s[1][n]中记录了矩阵链的最优括号化方案。
根据上述步骤,可以得到如下矩阵m和矩阵s: