二叉排序树
一、二叉排序树的定义(二叉排序树可用于元素的有序组织、搜索)
二叉排序树,又称二叉查找树(BST,Binary Search Tree)
性质:左子树结点值 < 根结点值 < 右子树结点值,左子树和右子树又各是一颗二叉排序树,
进行中序遍历(左根右),可以得到一个递增的有序序列
二、查找操作
1.定义
//二叉排序树结点
typedef struct BSTNode{int key;struct BSTNode *lchild, *rchild;
}BSTNode, *BSTree;
2.算法思想
若树非空,目标值与根结点的值比较:
若相等,则查找成功;
若小于根结点,则在左子树查找,否则在右子树查找。
查找成功,返回结点指针;查找失败返回NULL
3.代码实现(非递归实现)
最坏空间复杂度O(1)
//在二叉排序树种查找值为key的结点
BSTSearch1
4.代码实现(递归实现)
最坏时间复杂度O(h)
//在二叉排序树种查找值为key的结点
BSTSearch2
三、插入操作
1.算法思想
若原二叉排序树为空,则直接插入结点;否则,若关键字k小于根结点值,则插入到左子树,若关键字k大于根结点值,则插入到右子树
2.代码实现(递归实现)
最坏空间复杂度O(h)
//树中存在相同关键字的结点,插入失败
//新插入的结点一定是叶子
//在二叉排序树插入关键字为k的新结点(递归实现)
BSTInsert
3.代码实现(非递归实现)
//在二叉排序树插入关键字为k的新结点(递归实现)
BSTInsert
四、二叉排序树的构造
例1:按照序列str={50,66,60,26,21,30,70,68}建立BST
例2:按照序列str={50,26,21,30,66,60,70,68}建立BST(不同的关键字序列可能得到同款二叉排序树)
例3:按照序列str={26,21,30,50,60,66,68,70}建立BST(也可能得到不同款二叉排序树)
//按照str[]中的关键字序列建立二叉排序树
CreatBST
五、删除操作(重点)
1.算法思想
先搜索找到目标结点:
- 若被删除结点z是叶结点,则直接删除,不会破坏二叉排序树的性质。
- 若结点z只有一棵左子树或右子树,则让z的子树成为z父节点的子树,代替z的位置。
- 若结点z有左、右两棵子树,则令z的直接后继(或直接前驱)代替z,然后从二叉排序树种删去这个直接后继(或直接前驱),这样就转换成了第一或第二种情况。
左子树结点值 < 根结点值 < 右子树结点值
进行中序遍历,可以得到一个递增的有序序列
中序遍历
左 根 右
左 根 (左 根 右)
左 根 ((左 根 右) 左 根 右)
z的后继:z的右子树中最左下结点(该结点一定没有左子树)
左 根 右
(左 根 右) 根 右
(左 根 (左 根 右)) 根 右
z的前驱:z的左子树中最右下结点(该结点一定没有右子树)
六、查找效率分析(重点)
查找长度 – 在查找运算中,需要对比关键字的次数称为查找长度,反映了查找操作时间复杂度
若树高h,找到最下层的一个结点需要对比h次
最好情况:n个结点的二叉树最小高度为[log2n]向下取整+1。平均查找长度=O(log2n)
最坏情况:每个结点只有一个分支,树高h=结点数n,平均查找长度=O(n)
查找成功的平均查找长度ASL(Average Search Length)
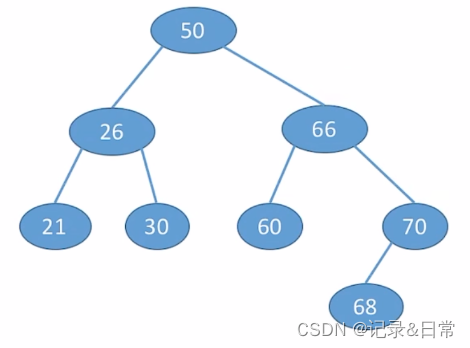
ASL 成功= (1 * 1 +2 * 2 +3 * 4 + 4 * 1) / 8 = 2.625
查找失败的平均查找长度ASL(Average Search Length)
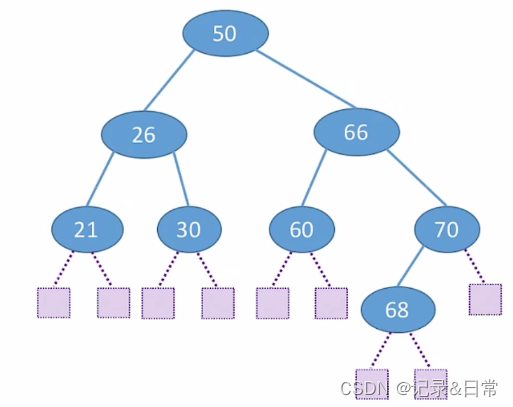
ASL失败=(3 * 7 + 4 * 2) / 9 = 3.22
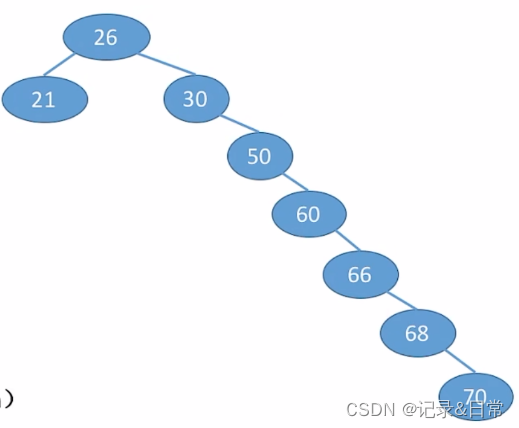
ASL成功 = (1 *1 + 2 * 2 + 3 * 1 +4 * 1 + 5 * 1 + 6 * 1 + 7 * 1) / 8 = 3.75
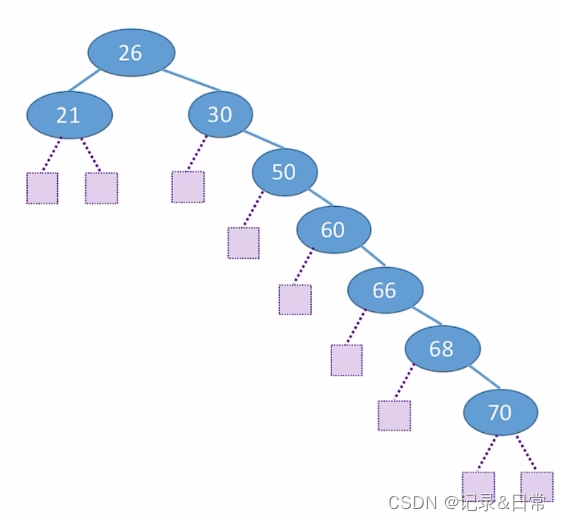
ASL失败 = (2 * 3 + 3+ 4 + 5+ 6 +7 * 2) / 9 = 4.22