别把自己太当回事，要把你做的事当回事！💓💓💓

1、问题描述

【问题描述】设计一个一元稀疏多项式得简单计算器。
【基本要求】采用带头结点的单链表存储一元稀疏多项式，设计实现简单计算器以下基本功能。
（1）输入并且建立多项式。
（2）一元多项式的相加运算。
（3）一元多项式的相减运算。
（4）一元多项式的相乘运算。
（5）一元多项式的求导运算。

👇👇👇
💘💘💘知识连线时刻（直接点击即可）

  🎉🎉🎉复习回顾🎉🎉🎉
    链表复习回顾

【测试数据】
输入数据：第一个多项式A，共5项，分别是（6，0）（2，1）（8，7）（4，15）（3，18）；第二个多项式B，共3项，分别是（7，1）（2，6）（-8，7）。
输出数据：
A多项式的结果：6 + 2X + 8X ^ 7 + 4X ^ 15 + 3X ^ 18
B多项式的结果：7X + 2X ^ 6 - 8X ^ 7
多项式A + B的结果：6 + 9X + 2X ^ 6 + 4X ^ 15 + 3X ^ 18
多项式A - B的结果：6 - 5X - 2X ^ 6 + 16X ^ 7 + 4X ^ 15 + 3X ^ 18
多项式A * B的结果：42X + 14X ^ 2 + 12X ^ 6 - 44X ^ 7 + 40X ^ 8 + 16X ^ 13 - 64X ^ 14 + 28X ^ 16 + 21X ^ 19 + 8X ^ 21 - 32X ^ 22 + 6X ^ 24 - 24X ^ 25
多项式A的导数结果：2 + 56X ^ 6 + 60X ^ 14 + 54X ^ 17

2、问题分析

这里小编提供一种思路哈：
1、首先我们要清楚这是需要建立带哨兵位头节点的单链表；每个节点里面存两个数据，一个是指数，一个是系数。
2、其次就是需要注意多项式输出的时候需要注意的各种情况，这里需要考虑完整，例如：系数小于0时，指数为1时等等。
3、接下来就到了，多项式计算环节，这里就需要用到数学上计算功底了，这里面需要注意。

3、源代码图解分析

具体细节操作还得看源码：（小编这里先拿图片对各个分文件里面重要环节做详解，之后再附上完整源代码）

首先看头文件中的代码：（Many.h）

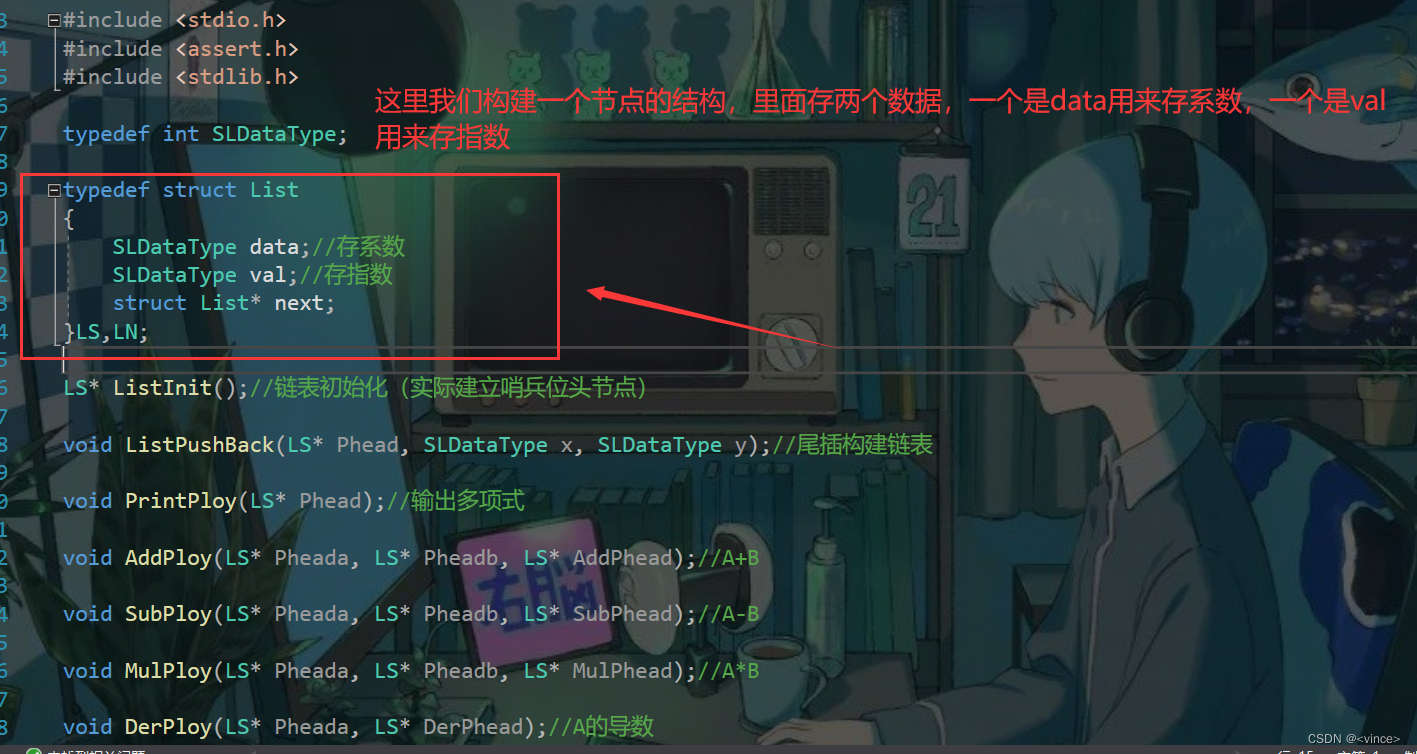
其次来看看源文件：（Many.cpp)

输出打印多项式函数：

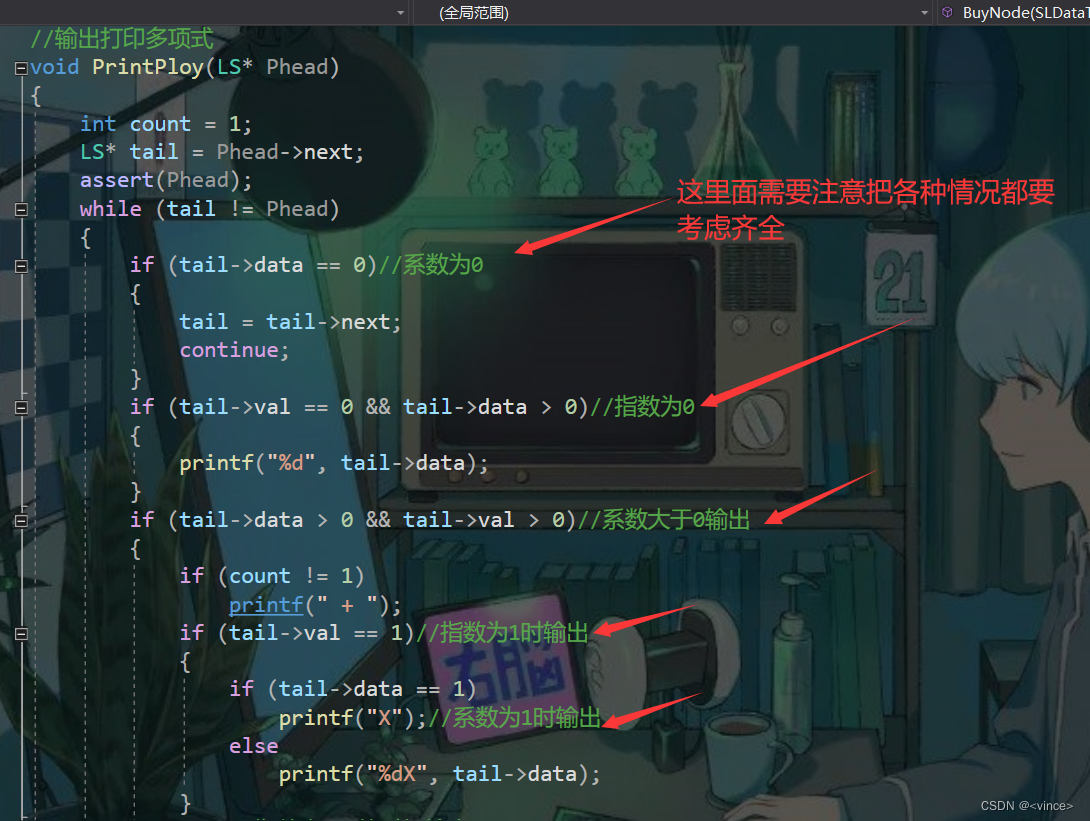
插多项式入函数：

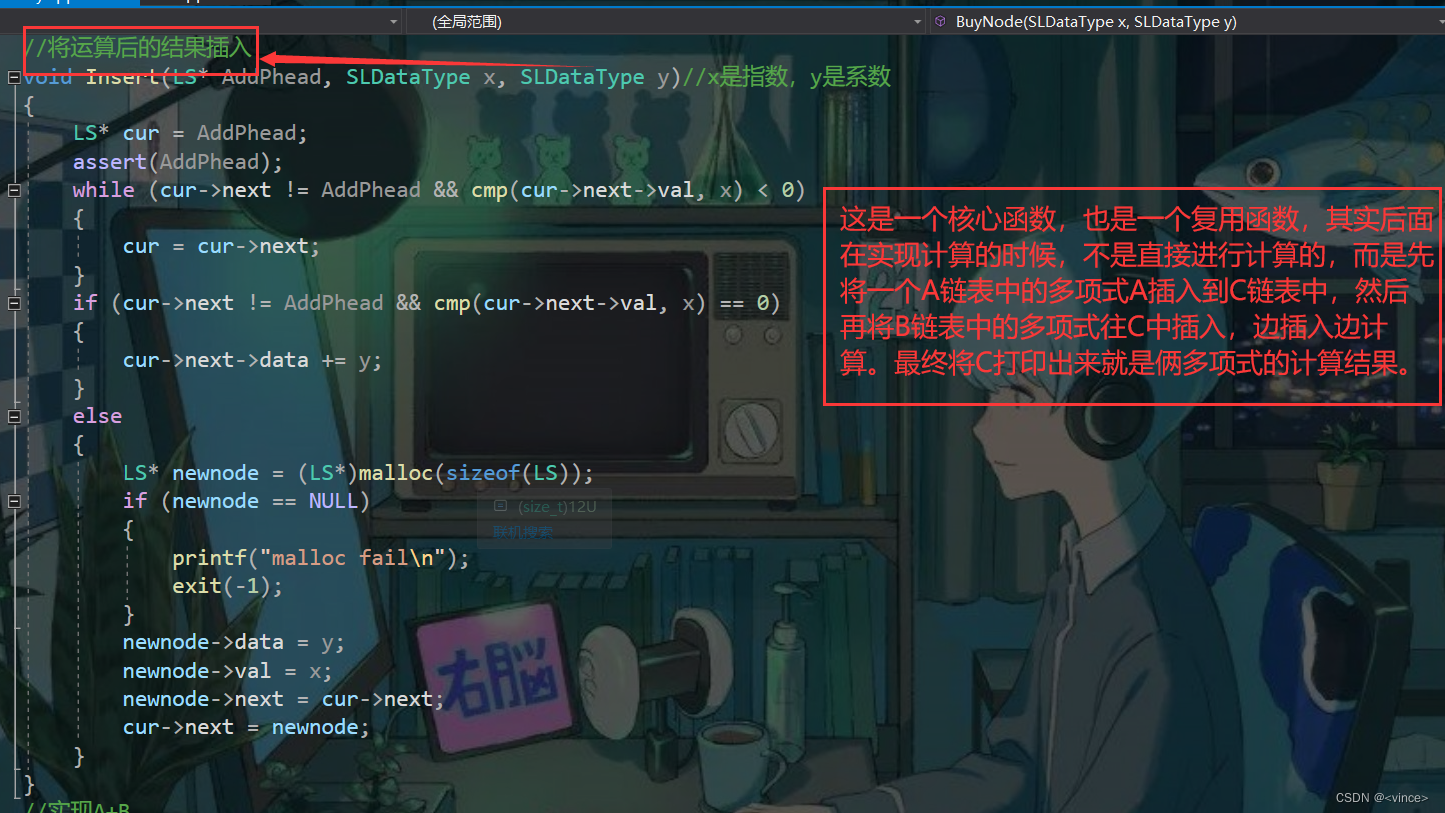
A+B函数：

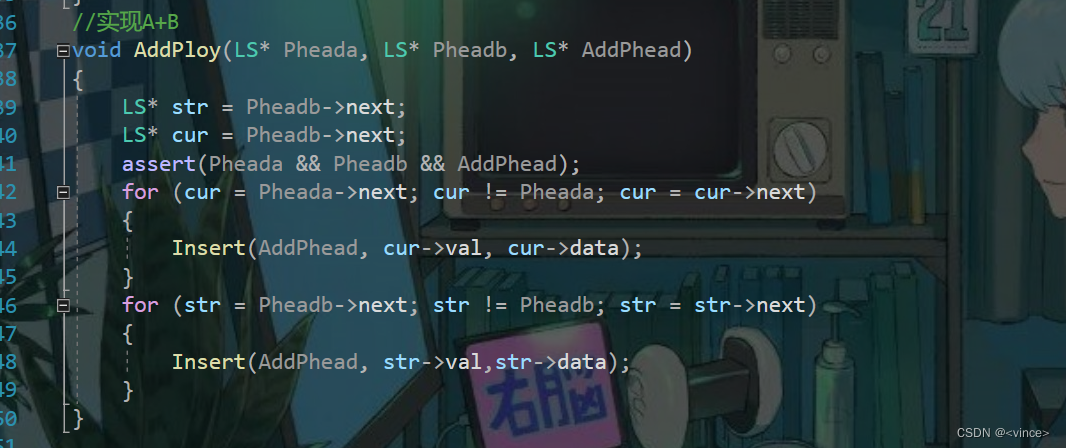
A-B函数：

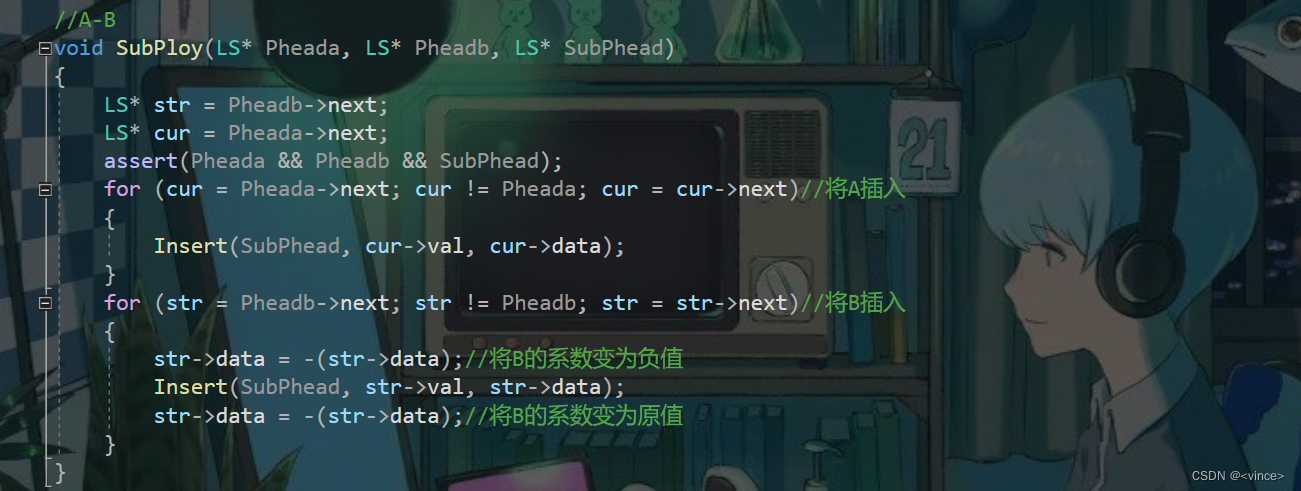
A*B函数：

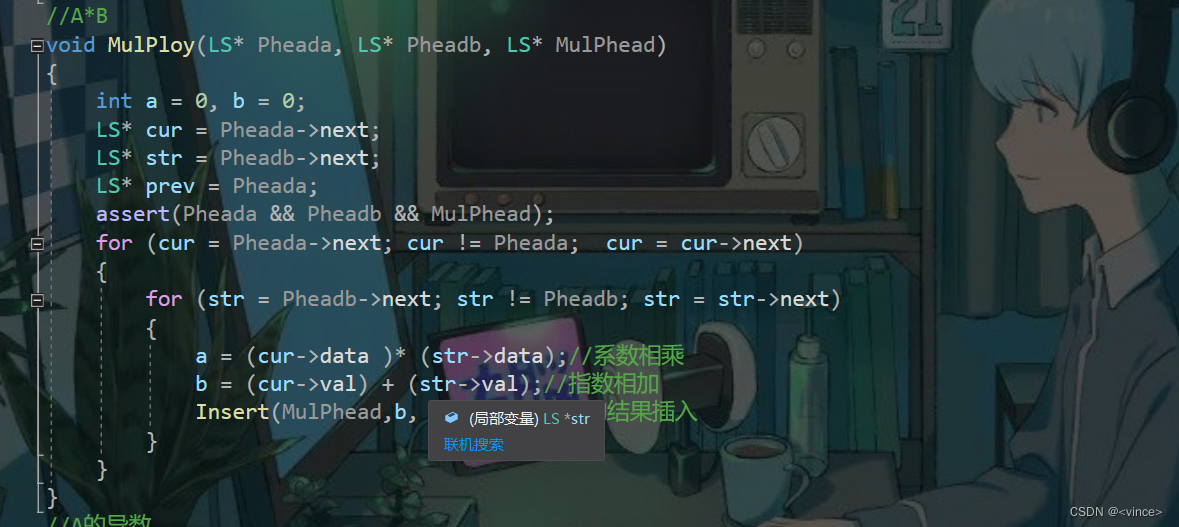
A的导数函数：

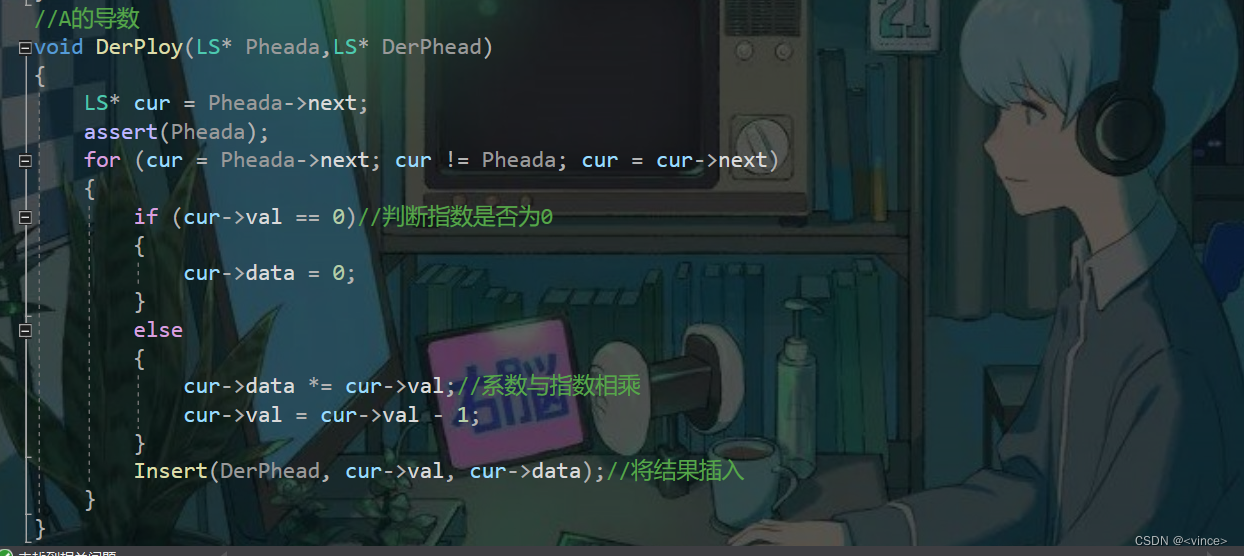
最后是主函数源代码（test.cpp）

4、完整源代码

上面的图解分析，小编是对该程序分文件操作，然后小编对其每个文件中重点函数进行分析展现，这里为了大家方便看源代码，小编也将其放在一个源文件中并且依然能正确运行：

#include <stdio.h>
#include <assert.h>
#include <stdlib.h>typedef int SLDataType;typedef struct List
{SLDataType data;//存系数SLDataType val;//存指数struct List* next;
}LS, LN;LS* ListInit();//链表初始化（实际建立哨兵位头节点）void ListPushBack(LS* Phead, SLDataType x, SLDataType y);//尾插构建链表void PrintPloy(LS* Phead);//输出多项式void AddPloy(LS* Pheada, LS* Pheadb, LS* AddPhead);//A+Bvoid SubPloy(LS* Pheada, LS* Pheadb, LS* SubPhead);//A-Bvoid MulPloy(LS* Pheada, LS* Pheadb, LS* MulPhead);//A*Bvoid DerPloy(LS* Pheada, LS* DerPhead);//A的导数//创建结点
LS* BuyNode(SLDataType x, SLDataType y)
{LS* newnode = (LS*)malloc(sizeof(LS));if (newnode == NULL){printf("malloc fail\n");exit(-1);}newnode->data = x;//存系数newnode->val = y;//存指数newnode->next = NULL;return newnode;
}//初始化建立哨兵位头节点
LS* ListInit()
{LS* Phead = BuyNode(0, 0);Phead->next = Phead;return Phead;
}
//尾插构建链表
void ListPushBack(LS* Phead, SLDataType x, SLDataType y)
{assert(Phead);LS* newnode = BuyNode(x, y);//单向循环，因此找尾部LS* tail = Phead->next;while (tail->next != Phead){tail = tail->next;}tail->next = newnode;newnode->next = Phead;
}
//输出打印多项式
void PrintPloy(LS* Phead)
{int count = 1;LS* tail = Phead->next;assert(Phead);while (tail != Phead){if (tail->data == 0)//系数为0{tail = tail->next;continue;}if (tail->val == 0 )//指数为0{printf("%d", tail->data);}if (tail->data > 0 && tail->val > 0)//系数大于0输出{if (count != 1)printf(" + ");if (tail->val == 1)//指数为1时输出{if (tail->data == 1.0)printf("X");//系数为1时输出elseprintf("%dX", tail->data);}else//指数大于1的时候输出{if (tail->data == 1.0)printf("X^%d", tail->val);elseprintf("%dX^%d", tail->data, tail->val);}}if (tail->data < 0 && tail->val > 0)//系数小于0输出{if (count != 1)printf(" - ");if (tail->val == 1)//指数为1时输出{if (tail->data == 1.0)printf("X");//系数为1时输出elseprintf("%dX", tail->data * (-1));}else//指数大于1的时候输出{if (tail->data == 1.0)printf("X^%d", tail->val);elseprintf("%dX^%d", tail->data * (-1), tail->val);}}count = 0;tail = tail->next;}
}int cmp(SLDataType a, SLDataType b)
{if (a > b)return 1;else if (a == b)return 0;elsereturn -1;
}
//将运算后的结果插入
void Insert(LS* AddPhead, SLDataType x, SLDataType y)//x是指数，y是系数
{LS* cur = AddPhead;assert(AddPhead);while (cur->next != AddPhead && cmp(cur->next->val, x) < 0){cur = cur->next;}if (cur->next != AddPhead && cmp(cur->next->val, x) == 0){cur->next->data += y;}else{LS* newnode = (LS*)malloc(sizeof(LS));if (newnode == NULL){printf("malloc fail\n");exit(-1);}newnode->data = y;newnode->val = x;newnode->next = cur->next;cur->next = newnode;}
}
//实现A+B
void AddPloy(LS* Pheada, LS* Pheadb, LS* AddPhead)
{LS* str = Pheadb->next;LS* cur = Pheadb->next;assert(Pheada && Pheadb && AddPhead);for (cur = Pheada->next; cur != Pheada; cur = cur->next){Insert(AddPhead, cur->val, cur->data);}for (str = Pheadb->next; str != Pheadb; str = str->next){Insert(AddPhead, str->val, str->data);}
}//A-B
void SubPloy(LS* Pheada, LS* Pheadb, LS* SubPhead)
{LS* str = Pheadb->next;LS* cur = Pheada->next;assert(Pheada && Pheadb && SubPhead);for (cur = Pheada->next; cur != Pheada; cur = cur->next)//将A插入{Insert(SubPhead, cur->val, cur->data);}for (str = Pheadb->next; str != Pheadb; str = str->next)//将B插入{str->data = -(str->data);//将B的系数变为负值Insert(SubPhead, str->val, str->data);str->data = -(str->data);//将B的系数变为原值}
}
//A*B
void MulPloy(LS* Pheada, LS* Pheadb, LS* MulPhead)
{int a = 0, b = 0;LS* cur = Pheada->next;LS* str = Pheadb->next;LS* prev = Pheada;assert(Pheada && Pheadb && MulPhead);for (cur = Pheada->next; cur != Pheada; cur = cur->next){for (str = Pheadb->next; str != Pheadb; str = str->next){a = (cur->data) * (str->data);//系数相乘b = (cur->val) + (str->val);//指数相加Insert(MulPhead, b, a);//将运算后的结果插入}}
}
//A的导数
void DerPloy(LS* Pheada, LS* DerPhead)
{LS* cur = Pheada->next;assert(Pheada);for (cur = Pheada->next; cur != Pheada; cur = cur->next){if (cur->val == 0)//判断指数是否为0{cur->data = 0;}else{cur->data *= cur->val;//系数与指数相乘cur->val = cur->val - 1;}Insert(DerPhead, cur->val, cur->data);//将结果插入}
}int main()
{LS* Pa = ListInit();//存放A多项式LS* Pb = ListInit();//存放B多项式LS* Add = ListInit();//存放A+B多项式LS* Sub = ListInit();//存放A-B多项式LS* Mul = ListInit();//存放A*B多项式LS* Der = ListInit();//存放A的导数size_t n = 0, m = 0;int a = 0, b = 0, c = 0, d = 0;printf("A多项式的项数：");scanf("%d", &n);//A的项数for (size_t i = 1; i <= n; i++){printf("A多项式的第%d项系数和指数：", i);scanf("%d %d", &a, &b);ListPushBack(Pa, a, b);}printf("A多项式的输出：");PrintPloy(Pa);printf("\n");printf("B多项式的项数：");scanf("%d", &m);for (size_t i = 1; i <= m; i++){printf("B多项式的第%d项系数和指数：", i);scanf("%d %d", &c, &d);ListPushBack(Pb, c, d);}printf("B多项式的输出：");PrintPloy(Pb);printf("\n");AddPloy(Pa, Pb, Add);printf("多项式A+B的输出：");PrintPloy(Add);printf("\n");printf("多项式A-B的输出：");SubPloy(Pa, Pb, Sub);PrintPloy(Sub);printf("\n");printf("多项式A*B的输出：");MulPloy(Pa, Pb, Mul);PrintPloy(Mul);printf("\n");printf("多项式A的导数输出：");DerPloy(Pa, Der);PrintPloy(Der);printf("\n");return 0;
}

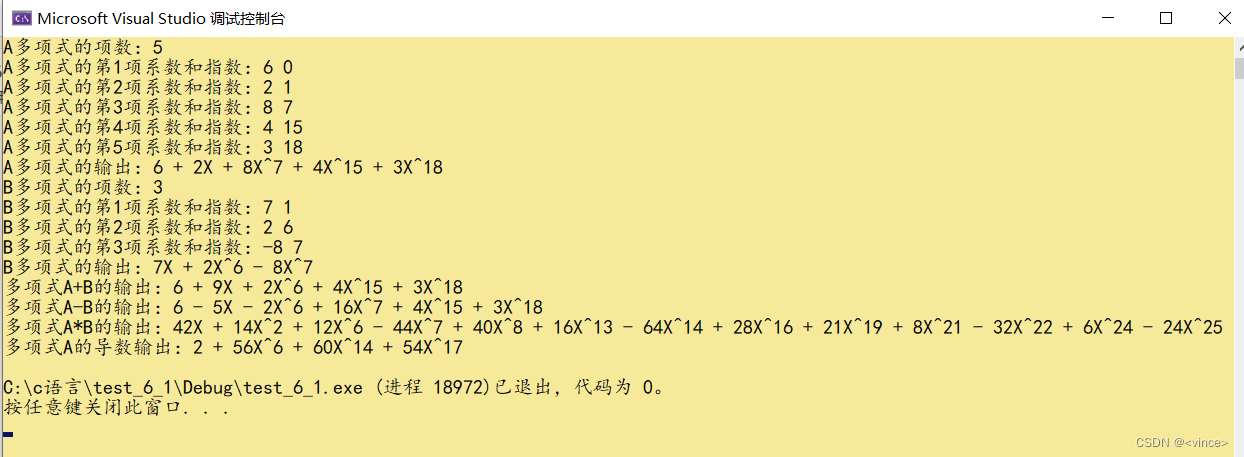
运行截图：

结语

这次也是一个小小的实验，是一元稀疏多项式计算器的实现，能够实现对两个多项式进行简单的计算处理即可。以上只是vince提供的一种方法，当然也还有很多不足之处，也望大家批评指正。

🎉🎉🎉以上代码均可运行，所用编译环境为 vs2019 ,运行时注意加上编译头文件#define _CRT_SECURE_NO_WARNINGS 1