问题描述

题目来源于1994年IOI信息学奥林匹克竞赛。
POJ1166 题目提交网址：http://poj.org/problem?id=1164
在这里插入图片描述
Figure 1 shows the map of a castle.Write a program that calculates

how many rooms the castle has
how big the largest room is

The castle is divided into m * n (m<=50, n<=50) square modules. Each such module can have between zero and four walls.
Input
Your program is to read from standard input. The first line contains the number of modules in the north-south direction and the number of modules in the east-west direction. In the following lines each module is described by a number (0 <= p <= 15). This number is the sum of: 1 (= wall to the west), 2 (= wall to the north), 4 (= wall to the east), 8 (= wall to the south). Inner walls are defined twice; a wall to the south in module 1,1 is also indicated as a wall to the north in module 2,1. The castle always has at least two rooms.
Output
Your program is to write to standard output: First the number of rooms, then the area of the largest room (counted in modules).
Sample Input
4
7
11 6 11 6 3 10 6
7 9 6 13 5 15 5
1 10 12 7 13 7 5
13 11 10 8 10 12 13
Sample Output
5
9

解决思路

把方块看成节点，相邻的两个方块如果之间没有墙，则在方块之间连接一条边，这样城堡就能转换成一个图。
题目中给出的“地图”即可转换为如下图所示的图，寻找城堡数即转换为寻找极大联通子图的数量。
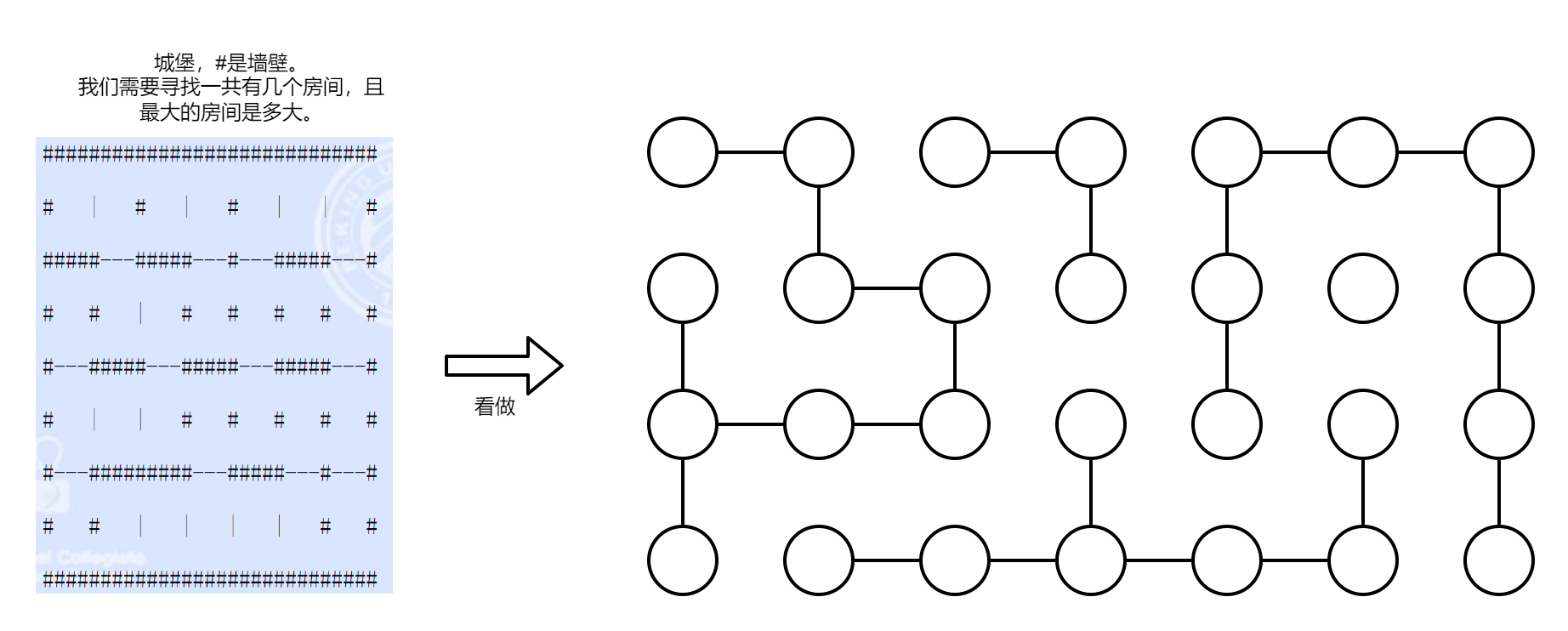
在这里插入图片描述

根据深度优先搜索的算法，从一个节点出发，便可以找到该节点的极大联通子图，并做标记（以防重复寻找），然后继续寻找下一个节点所在极大联通子图。

思路：依次对每一个节点（房间）开始进行深度优先搜索，给该节点的极大联通子图上色，并全部标记为旧节点，然后继续寻找下一个为被搜索的节点（房间）。
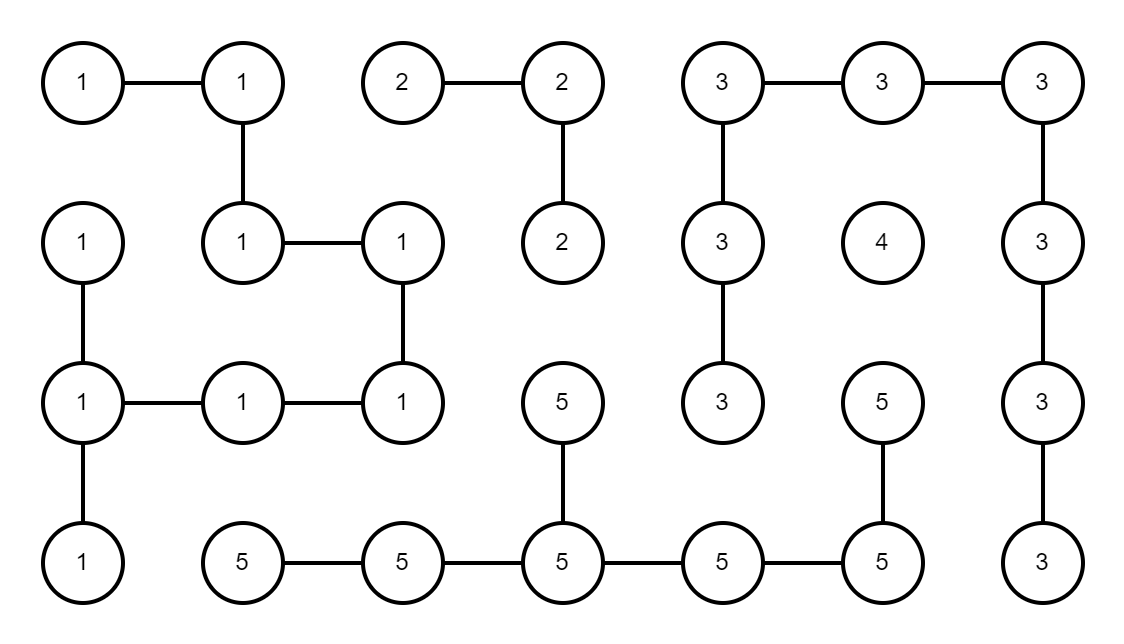
在这里插入图片描述
上图中可以看出一共有5个房间（极大联通子图），最大的有9个节点

DFS遍历图的递归算法框架

DFS(V){if(V是旧节点) return;将V标记为旧节点;对和V相邻的每个节点U{DFS(U);}
}
int main(){初始化;将所有节点标记为新点;while(图中能找到新点W){DFS(W);}
}

Java代码


import java.util.Scanner;public class Main {public static void main(String[] args) {Solution solution = new Main().new Solution();int R,C;Scanner scanner = new Scanner(System.in);R = scanner.nextInt(); // 几行C = scanner.nextInt(); // 几列int[][] rooms = new int[R][C];for (int i = 0; i < R; i++) {for (int j = 0; j < C; j++) {rooms[i][j] = scanner.nextInt();}}solution.solve(R,C,rooms);}class Solution{int R,C;int maxRoomArea = 0;int colorNum = 0;int roomArea = 0; // 用于临时记录个房间的大小int[][] colors,rooms; // rooms 原始房间地图  colors用于记录颜色（）public void solve(int R,int C,int[][] rooms){this.R = R;this.C = C;this.maxRoomArea = 0; // 最大房间的大小this.colorNum = 0; // 颜色序号，0为未上色（没有搜过），this.roomArea = 0;this.colors = new int[R][C]; // 默认初始化所有点为0this.rooms = rooms;for(int i = 0;i < R;i++){for(int j = 0;j < C;j++){if(colors[i][j]==0){ // 找到一个新节点colorNum++; // roomArea = 0;DFS(i,j);maxRoomArea = Math.max(maxRoomArea,roomArea);}}}System.out.println(colorNum);System.out.println(maxRoomArea);}public void DFS(int i,int j) {if(colors[i][j] != 0)return; // 旧点，返回colors[i][j] = colorNum; // 上色roomArea++; if(((rooms[i][j]) & 1) ==0) DFS(i,j-1); // 向左找if(((rooms[i][j]) & 2) ==0) DFS(i -1 ,j); // 向上找if(((rooms[i][j]) & 4) ==0) DFS(i,j+1); if(((rooms[i][j]) & 8) ==0) DFS(i + 1,j);}}
}