目录
01 说明
遥感影像的存储方式
BSQ方式
BIL方式
BIP方式
如何计算图像存储空间大小(字节数)?
简单的单位换算
计算公式
简单地
复杂地
如何查看影像的基本信息/辅助信息?
如何进行直方图的阈值分割?
辐射校正
系统辐射校正
是什么
怎么做
为什么要做
辐射定标
是什么
怎么做
为什么要做
大气校正
是什么
怎么做
为什么要做
地表辐射校正(地面辐射校正)
是什么
怎么做
为什么要做
辐射校正和辐射增强区别
辐射校正的原因、误差是什么
辐射校正和大气校正之后我们会得到一个什么样的数据?得到这个数据之后还要做一些什么工作?
几何校正
是什么
怎么做(方法)
多项式模型中控制点的个数如何求取?
控制点如何选取?原则是什么?
为什么要做
什么时候做
图像变换
傅里叶变换
波段运算
K-L变换
K-T变换(缨帽变换)
K-L变换和K-T变换的特征以及如何区分?
最近邻内插和双线性内插怎么计算?
最近邻内插
双线性内插
彩色变换
图像滤波
对比度计算
辐射增强-直方图匹配(直方图规定化)和直方图均衡化
是什么
使用条件
小知识点
空间域中的平滑去噪-中值滤波+均值滤波的计算
边缘增强
图像分割和图像分类
图像分割的作用
图像分割的计算方法
灰度阈值法
梯度方法
区域方法
数学形态学方法
遥感影像的地物分类,如何判断特征空间分成几类地物?
Kappa系数
监督分类和非监督分类的常见算法及其特征
监督分类
非监督分类
分类结果的改善
遥感数字图像处理课程包含了哪几块的内容(思考题)
01 说明
由于资料在word中,搬运中存在格式混乱。
上机及上机考试占50%
期末考试占50%
选择题10题-每题2分
判断题5题-每题2分
简答题两题-每题15分(每题3~4问)
计算题一题
概述题一题
-
遥感影像的存储方式
-
BSQ方式
-
存储方式:BSQ(Band sequential)是像素按波段顺序依次排列的数据格式,即先按照波段顺序分块排列,在每一个波段块中,再按行列顺序进行排列。逐波段存储(BSQ)保证了像素空间位置的连续性,有利于图像空间分布信息的显示与处理。

-
-
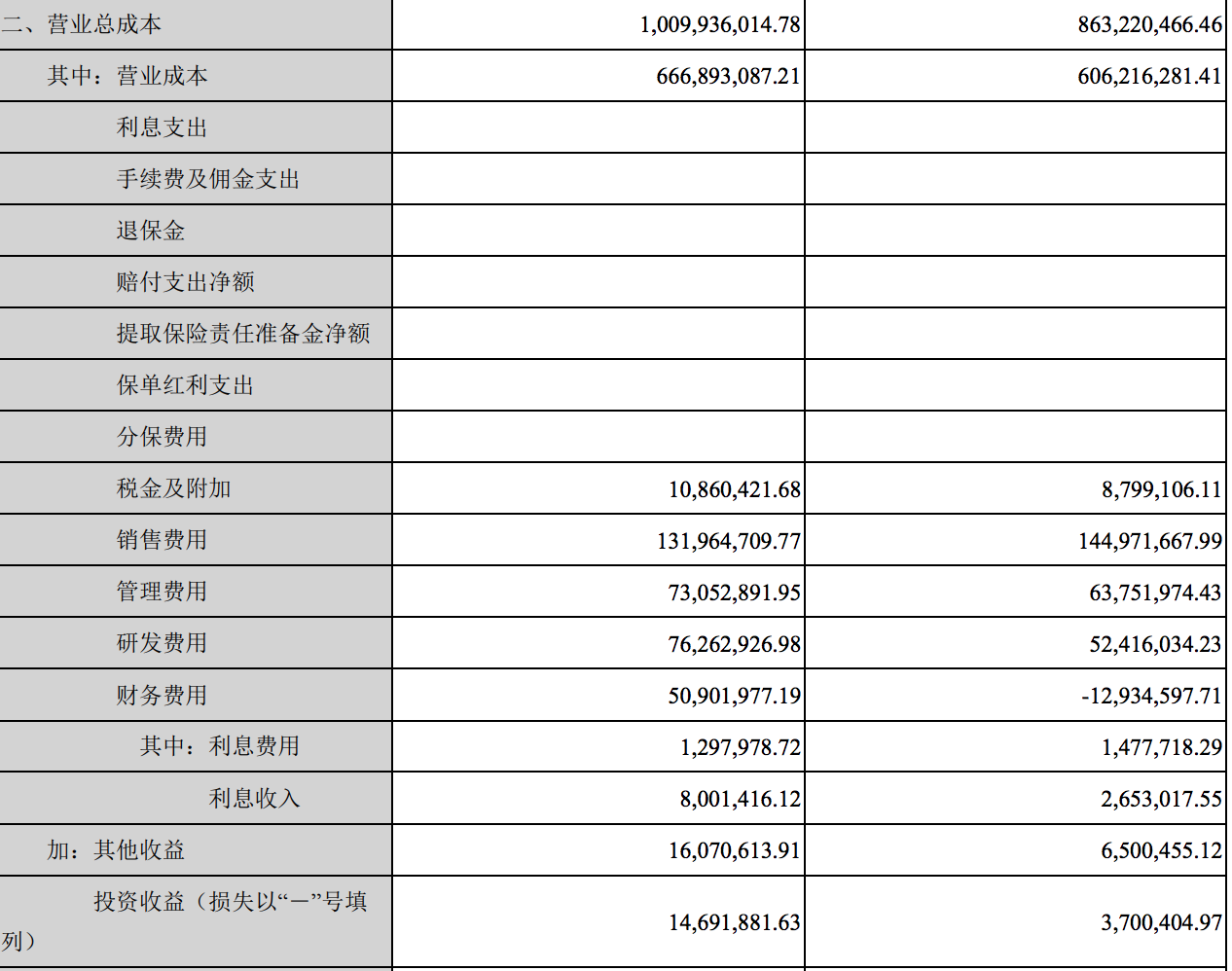
BIL方式
-
存储方式:像素先以行为单位分块,在每一个块中,按照波段顺序进行像素排列,同一行不同波段的数据保存在一个数据块中。逐行存储(BIL)兼顾了图像空间分布信息与像元光谱信息的显示与处理。
-
-
BIP方式
-
存储方式:以像素为核心,同一像素不同波段数据保存在一起,打破了像素空间的连续性。每一个块为当前像素不同波段的像素值。逐像元存储(BIP)有利于图像元光谱信息的显示与处理。

-
如何计算图像存储空间大小(字节数)?
-
简单的单位换算
-
1B = 8b
关键在于此,B表示字节数(亦称之为Byte);b表示比特(亦称之为bit)
1KB = 1024 B
1MB = 1024KB
-
-
计算公式
-
简单地
-
-
一幅影像的所需比特数b = r * s * k;
其中,r表示影像行数(raw),s表示影像列数(sample),k为量化位数,与影像的灰度级数相关,即L = 2k(例256 = 28)。
故一幅影像的字节数:

例如:一幅600行800列像元级数为256的遥感影像的存储空间大小为:
600 * 800 * 8 = 3840000 bit = 480000 B = 468.75 KB
-
-
-
复杂地
-
-
或者说,标准地,我们图像文件大小地计算应如下:

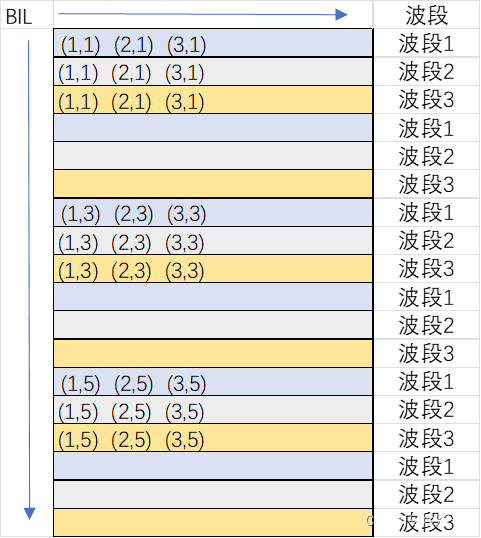
在该公式中,文件大小的单位为B(字节数)。其中,每一个像素的字节数与前文的k不同,k表示每一个像素的比特位数,二者之间的关系其实就是:
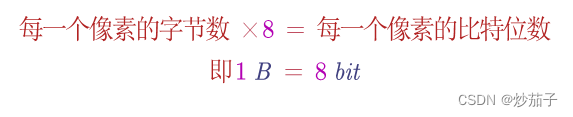
例如灰度量化级数为0~255,那么共有256=28,我们需要使用8位二进制数才可以表示0~255的任意数值。因此比特位数位8,由于单位换算,8bit=1b,因此每一个像素所占字节数为1,每一个像素的比特位数位8。
而对于辅助参数,一般题目给定,若不给定,默认为1即可。
-
如何查看影像的基本信息/辅助信息?
如果不是原始的遥感影像,而是ENVI标准格式的文件,那么在头文件(.hdr)中可以进行查看;
更多地,如果是原始地遥感影像,一般是有辅助文件,但是不同卫星的辅助文件各不相同,对于Landsat影像,其辅助文件为*_MTL.txt文件;对于环境卫星,辅助文件为.XML文件;对于Modis,其更多镶嵌在HDF文件的属性、波段中;
当然。或许我们会将这些包括图像获取的日期和时间(一般会存在两个时间,一个是影像拍摄的时间,另外一个是影像拍摄后在地面站进行预处理制作成产品(也就是现在你手头上的这个文件)的时间)、投影参数(例如基准面、仿射变换参数等)、几何纠正精度、几何分辨率(例如30m分辨率)、辐射校正参数(一般是辐射定标所需要的系数和偏置)等的辅助文件统一称之为元数据。
- 如何绘制影像的直方图?
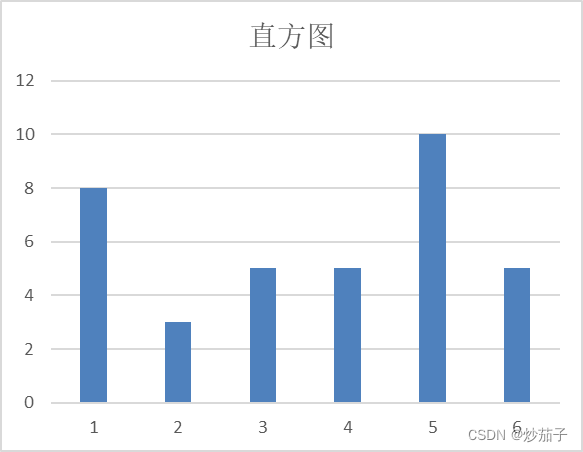
绘制前,我们讲讲直方图的概念,直方图是灰度级的函数,描述的是图像中各个灰度级的像素个数。其依据图像像素的灰度级范围,以横轴为灰度级,以纵轴表示每一灰度级具有的像素数或者是该像素占总像素的比例值。
现在以随机生成的一张影像为例说明直方图的绘制。
说明:上述影像中,每一个表格表示一个像元,表格上的数值表示该位置像元值。
首先,我们需要统计各个数值出现的频数,统计如下:

绘制的直方图如下:

-
如何进行直方图的阈值分割?
首先,我们需要明白图像分割是什么?
一幅图象通常是由代表物体的图案与背景组成,简称物体与背景。若想从一幅图象中“提取”物体,可以设法用专门的方法标出属于该物体的点,如把物体上的点标为“1”,而把背景点标为“0”,通过分割以后,可得一幅二值图象。
例如,我们想要提取一幅影像中的云,那么云就是代表物体的图像,其余均为背景,这实际上就是一个二分类。
而直方图的阈值分割的原理就是,我们要提取的物体与其它背景是存在差别的,这种差别在直方图上就是灰度值的分布不同。
例如下方:

当我们想要图像中的水体提取出来时,我们通过计算NDWI指数并绘制了直方图如上。我们知道,NDWI指数高的的位置更有可能为水体,因此我们有理由怀疑右侧小波峰处大概率为水体,而其它位置特别是左侧的波峰我们认为它是背景,那么将二者区分开来自然就是在中间切一刀。
切一刀就是在直方图上进行阈值分割,例如这里阈值为0.18,因此我们将 像元灰度值(NDWI指数)小于0.18认为是背景,像元灰度值(NDWI指数)大于0.18的像元认为是水体,如此实际上就是对图像进行了二值化处理,也就是我们常说的重分类。
总而言之,我们使用直方图进行阈值分割,一定是在波谷进行阈值分割,而不是在波峰进行阈值分割,这是常识。
- 如何绘制某一波段的光谱曲线?
似乎表述有错误?若按ENVI中光谱曲线的绘制
若有多个波段,那么可以绘制Z光谱曲线,即某一像元不同波段(波长)的像元折线图è光谱曲线图;如下:

若是仅有一个波段,那么可以绘制水平方向上的光谱曲线;

也可以绘制垂直方向上的光谱曲线:
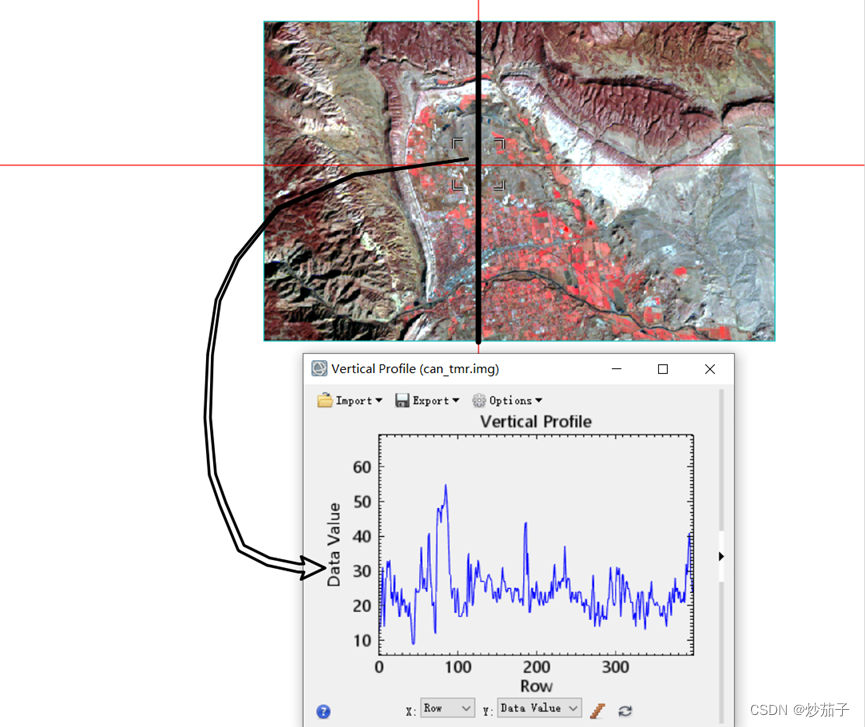
至于某一波段的光谱曲线如何绘制,这里暂无。
-
辐射校正
首先说说辐射校正的整个流程吧。
我整理了一些,大致流程应如下:

首先,由于卫星上本身系统例如传感器光学器件等造成的系统误差,我们需要进行消除,这一部分在地面站点已经进行了处理,一般不需要用户进行处理除非改进。
接着,我们若是拿到一级产品等,(有时)我们需要对影像进行辐射定标,这一步实际上就是将传感器中接收的电信号(DN值,像素值的通用术语是数字量化值或DN值,它通常被用来描述还没有校准到具有意义单位的像素值。)转化为有实际意义的辐射亮度或者反射率等(注意此处均是大气顶部的测得的数值即包含了大气的影响);为什么说它包含了大气的影响呢?因为此时的影像仅仅是地表目标物辐射的能量经过大气到达传感器被其接收而得到的影像,而我们此处的辐射定标也仅仅是将这些能量进行简单的变换,而能量本身并不是地物本身辐射的能量了。例如,我们有一个小人A,辐射的能量是100J,经过大气之后,存在大气散射,可能消失了20J,最终到达传感器的能量就是80J了,我们假定影像上某一像元位置即是该小人A的值80J,那么我们辐射定标实际上就是将该80J转化为反射率例如0.4.但是其本质上还是包含了大气的影响。此处省略了其它成分,仅仅着重展示了大气在其中扮演的角色。
接着,由于我们知道了大气对我们影像产生的影响,因此我们尝试去消除大气影响例如大气散射而导致的一些误差,这种过程就称之为大气校正。由于大气校正本身原理比较复杂,这里不进行说明。
进行完大气校正之后,一般我们就可以拿来使用了。而至于此处的地面辐射校正,其实基本上我是没有做过的,一是有一些数据没有相关参数例如太阳高度角等,二是没有相关教程说明(甚少),或许在地面站点就已经做过了也不一定。另外需要注意,此处进行由于地形起伏引起的校正实际上还是针对像元值进行的辐射校正而非对像元位置的校正。
-
-
系统辐射校正
-
是什么
-
-
对传感器成像系统造成的系统误差进行的粗校正称之为系统辐射校正。
-
-
-
怎么做
-
-
对光学镜头的非均匀性引起的边缘减光现象进行校正;
对由检测器等引起的坏线和条纹进行修复;
通过域值法识别坏像元,并通过平滑操作以进行斑点的修复;
-
-
-
为什么要做
-
-
因为影像存在边缘减光现象、条纹坏线、斑点等问题时,会对影像目视解译等产生影响。
-
-
辐射定标
-
是什么
-
-
辐射定标一般而言是将传感器记录的电压或数字量化值(DN值)转换成辐射亮度、反射率等遥感物理量的过程。
-
-
-
怎么做
-
-
理论公式复杂,我们直接使用实操的公式:

或者:

以上公式中的增益系数、偏置、最小最大值等一般仅针对影像中某一波段而言,因为不同波段的计算公式参数不同。
-
-
-
为什么要做
-
-
为了消除传感器本身的误差,确定传感器入口处的准确辐射值,将DN值转换为辐射亮度值、反射率值和温度等物理量
-
-
大气校正
-
是什么
-
-
消除由大气散射等引起的辐射误差的处理过程称之为大气校正。
-
-
-
怎么做
-
-
对于可见光和近红外波段,我们使用ENVI的Flaash等模块进行大气校正;
对于热红外波段,由于我们不需要考虑大气的散射而考虑其吸收和发射,因此我们使用ENVI的Thermal Atm Correction等进行热红外波段的大气校正。
-
-
-
为什么要做
-
-
消除大气和光照等因素对地物反射的影响,获得真实地表反射率、辐射率、地表温度等真实物理模型参数。
-
-
地表辐射校正(地面辐射校正)
-
是什么
-
-
地面辐射校正包括太阳辐射校正和地形辐射校正。
太阳辐射校正的目的是通过将太阳光线倾斜照射时获取的图像校正为太阳光线垂直照射时获取的图像。(主要用于比较不同太阳高度角的图像,消除不同地方、不同季节、不同时期图像之间的辐射差异,通常通过调整图像的平均亮度加以实现。)
地形辐射校正的目的是消除由地形引起的辐射亮度误差,使坡度不同但反射性质相同的地物在图像中具有相同的亮度值。
(链接:https://www.zhihu.com/question/438245884/answer/2349543187)
-
-
-
怎么做
-
-
无
-
-
-
为什么要做
-
-
消除由太阳高度角等和地形起伏引起的辐射亮度误差。
-
-
辐射校正和辐射增强区别
-
辐射校正是一种预处理步骤,其目标是去除影像中由于传感器特性、观测条件和大气效应等非地表目标因素引起的辐射畸变,从而获取地表真实的反射率或辐射亮度。辐射校正包括系统辐射校正、辐射定标、大气校正、地面辐射校正(太阳辐射校正和地形辐射校正)等步骤。
辐射增强则是一种后处理步骤,其目标是通过调整影像的灰度级别,提高影像的视觉质量和解译效果。辐射增强的方法通常包括直方图均衡化、直方图规定❀、线性拉伸、非线性拉伸等,它们可以改变影像的对比度和亮度,使得人眼或计算机更容易从影像中提取信息。
所以,辐射校正和辐射增强的主要区别在于,前者试图恢复地表的真实辐射信息,而后者试图改善影像的视觉效果,使得信息更容易被解读。
-
-
辐射校正的原因、误差是什么
-
由于传感器自身的因素(比如传感器老化、暗电流、损坏像元等,都可能引起影像辐射信息的误差)以及大气状况(地球大气会吸收和散射来自地表的太阳辐射,这会影响卫星接收到的辐射值)、太阳位置(不同的观测角度和太阳高度角会使得同一地物的反射率或辐射亮度表现不同)、地形起伏(地形因素例如坡度坡向导致影像辐亮度的变化)等外界因素,使得目标物反射或发射的能量与传感器的测量值存在差异。
-
-
辐射校正和大气校正之后我们会得到一个什么样的数据?得到这个数据之后还要做一些什么工作?
-
这里没有找到相关的解答。那就随便答吧。
首先,要明白这里的辐射校正应该是老师口误,因为至少在国内的教材中辐射校正大多包含了辐射定标、大气校正等;但是我们在进行一些数据集特别是国外数据集的下载中,常常引发一些错误,因为国外的Radiometric calibration(实际上其为辐射定标)有时翻译为辐射校正,而Radiometric correction(实际为辐射校正)也翻译为辐射校正。也有的数据集的介绍进行混用,这会导致一些混乱。当然,也有一些人不满教材中如此阐述,不过已是大势所趋了。
因此应该是进行辐射定标和大气校正后,我们会得到一个什么样的数据?对于这个数据之后还要进行哪些工作?
首先,我们得到的数据是关于真实地表反射率、辐射率、地表温度等遥感物理量的影像。
得到这个数据之后我们需要对影像进行几何校正。
-
几何校正
-
是什么
-
几何校正是指消除或改正遥感影像几何误差的过程。
-
-
怎么做(方法)
-
几何校正包括正射校正、几何粗校正(地面站点就已完成)、几何精校正(几何配准、地理配准等均是指代其)。
当然应该也包括重采样,这其实也就解释了为什么我们是先做辐射校正然后再进行几何校正。原本二者本无任何关联,辐射校正解决的是像元值的问题,而几何校正解决的是像元位置的问题,进行辐射校正仅仅只会对影像中各个像元的像素值进行变换,而不会对像元位置进行变换。但是问题就在于此,我们在进行几何校正之后,由于进行了重采样(因为像元位置发生了变化,可能存在有一些位置处空缺像元,因此需要重采样),那么就会导致像元值发生变化。当然,影响也不是特别大,你想要反着来操作也不会有太大的影响,但是大家都这么操作,而且确实事出有因那就没有必要如此。
-
-
-
多项式模型中控制点的个数如何求取?
-
-
既然老师强调多项式模型,也强调了几何校正如何去做,那么我们就通过多项式模型了解几何校正的大致原理,当然最重要的还是控制点的个数如何求取,毕竟这是考试。我们知道,几何校正的本质就是将像元校正到正确的位置上去。
那么多项式模型如何解决这个问题呢?

那么,问题在于,怎么得到?
对于一次项模型(最高阶是1),我们的式子应如下:



-
-
-
控制点如何选取?原则是什么?
-
-
- 控制点应选取图像上易分辨且较精细的特征点,如道路交叉点、河流弯曲或分叉处、湖泊边缘、飞机场、城廓边缘等
- 地面控制点上的地物不随时间而变化,以保证当两幅不同时段的图像或地图几何纠正时,可以同时识别出来
- 特征变化大的地区应多选一些
- 图像边缘部分一定要选取控制点,以避免外推
- 尽可能满幅均匀选取
-
为什么要做
-
因为影像在成像过程中像元位置会受到以下方面的影响,造成影像发生几何畸变,因此需要通过几何校正将像元校正到正确的位置。
- 传感器成像方式引起的图像变形;
- 传感器外方位元素变化的影响;
- 遥感平台位置和运动状态变化的影响: 航高、航速、俯仰、翻滚、偏航;
- 地形起伏影响而产生的像点位移;
- 地球表面曲率的影响:一是产生像点位移;二是像元对应于地面宽度不等,距星下点愈远畸变愈大,对应地面长度越长;
- 大气折射的影响:产生像点位移;
- 地球自转引起的变形;
通过对各个影像进行几何校正,保证不同图像间的几何一致性
-
-
什么时候做
-
当需要将来自不同日期、传感器、平台、高度、视角等的遥感影像进行对比、融合、叠置分析等时,需要进行几何校正,以使所有影像在空间上对齐保证不同图像间的几何一致性
特别地,对于几何校正中地正射校正,一般在高分辨率影像需要进行(特别使亚米级)。
-
图像变换
-
傅里叶变换
-
不会具体考,只需要知道傅里叶变换是什么?
傅里叶变换是图像处理中一种有效而重要的方法,可用于图像特征提取、频率域滤波、周期性噪声去除、图像恢复、纹理分析等。
-
-
波段运算
-
类似栅格计算器,不进行阐述。
-
-
K-L变换
-

就可以得到K-L变换之后的影像了。当然,你或许会问,你前面说舍去某些行,可是我的影像是一个二维的,确实,事实上我们是将二维影像一维化,例如,我们有6个波段的一张影像,那么:

X一共6行表示6个波段的信息,进行主成分正变换得到Y,进行一些取舍之后(例如将后面三行全部变为0),再进行主成分逆变换得到新的X。那么现在的X就是去除了很多噪声的6波段影像。
在Y中,我们称一行就是一个主成分分量,我们根据Y的协方差矩阵可以知道各个分量的有效信息,如此进行取舍。
-
-
K-T变换(缨帽变换)
-
K-T变换实际上就是一种特殊的K-L变换,我们进行k-L变换可以得到最好的变换,就是在最大程度上将噪声或者说冗余部分去除了,但是我们K-L变换之后得到的各个分量却没有特别的含义或者说没有什么可比较性。
但是K-T变换在K-L的变换上进行了改进,K-T变换得到的各个主成分分量具有一定的景观含义。
对于Landsat MSS传感器而言:
第一个分量是亮度分量,是土壤反射率变化的方向;
第二个分量是绿色物质分量(绿度),反应植物的生物量状况;
第三个分量是黄色物质分量(黄度);反应植物的枯萎程度;
对于Landsat TM和ETM+传感器而言:
第一个分量是亮度,反应总体反射值(与MSS不同);
第二个分量是绿度,类似;
第三个分量是湿度;
不同的传感器,卫星的含义不尽相同。
至于缨帽变换的特征是什么?上面三个分量代表的含义需要谨记;另外就是它独立于影像,对于同一传感器其变换系数(就是我们前面讲的![]() 类似但是稍有差别吧)是固定的;
类似但是稍有差别吧)是固定的;
-
-
K-L变换和K-T变换的特征以及如何区分?
-
这里需要注意,对于K-L变换,每一张影像的变换矩阵(![]() )都是不一样的,它是根据影像中各个波段的栅格矩阵进行计算得到的;而对于K-T变换,它对于同一种传感器拍摄的影像,变换矩阵( )都是固定的;这应该算是二者的一个区别;
)都是不一样的,它是根据影像中各个波段的栅格矩阵进行计算得到的;而对于K-T变换,它对于同一种传感器拍摄的影像,变换矩阵( )都是固定的;这应该算是二者的一个区别;
如果说还有区别,那就是二者得到的分量,对于K-L变换得到的分量很难具有一定的特殊含义或比较含义;而对于K-T变换得到的三个分量具有明确的物理意义(例如我们可以利用第二和第三分量进行植被和水体信息的提取);
-
-
最近邻内插和双线性内插怎么计算?
-
以题为例:
若f(1,1)=1, f(1,2)=5, f(2,1)=3, f(2,2)=4, 分别按照最近邻插值法、双线性插值法确定点(1.2,1.6)的灰度值
-
-
-
最近邻内插
-
-
最近邻算法:要插值的像元点的值为距离其最近的已知像元的值。
在此题中,我们假定A(1,1)、B(1,2)、C(2,1)、D(2,2)、E(1.2,1.6),那么

可以发现,需要插值像元E(1.2,1.6)与已知像元B距离最近,因此我们认为E点(1.2,1.6)的灰度值为B点的灰度值即5。
-
-
-
双线性内插
-
-
有一点难这种算法,但是理解了就还好。其实就是进行了两次一次线性插值。
还是刚刚那道题(假设不变),我们一点一点剖析,如果我们知道了以下两个蓝点(F、G)的像元值,那么对于要插值的像元E我们是不是有一点思路了?
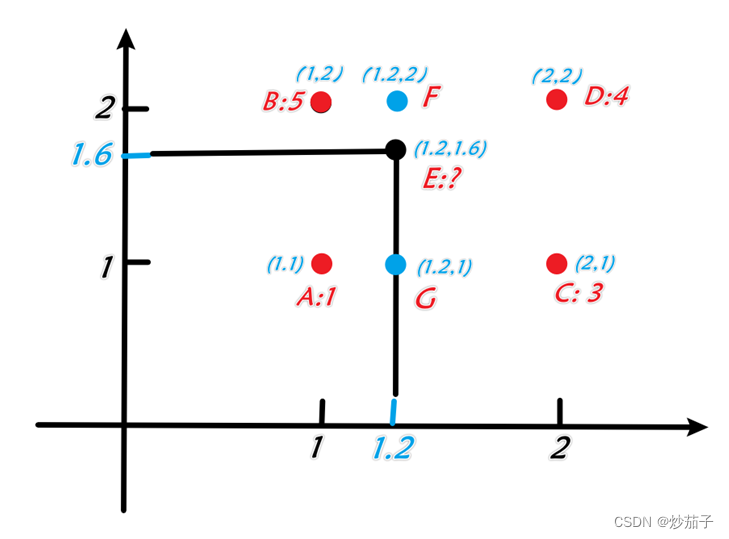
假定我们已知F点和G点的灰度值(不如称之为f(F)、f(G)),另外我们假定从F点到G点的灰度值是线性变化的,那么它灰度的线性变化不就是按照距离由大到小或者由小到大嘛,而我们要的E点就在其中,如此我们不是可以得到E点的灰度值?
一句话就是该点的值= 该点在横轴或者竖轴邻近小的那个点(坐标小的那个)的距离与该点在横轴或者纵轴相邻两点的距离的比值 * 相邻两点的灰度值之差 + 某一点的灰度值,某一点看下面的公式自然一眼懂。
那么这个线性变化用公式如何去表达?

如此可以计算出f(E) 的灰度值了。
那么问题来了,我如何求取F点和G点的灰度呢?类似的,我们还是进行如此计算,我就不详细阐述了,公式如下:

总共三个式子,三个未知数: 最终结算E点的灰度值为3.44.
最终结算E点的灰度值为3.44.
有的双线性内插喜欢这样子计算:
f(F)=5 + (4 - 5) * ((1.2 - 1) /(2 - 1)) = 4.8
f(G)=1 + (3 - 1) * ((1.2 - 1) /(2 - 1)) = 1.4
f(E) = 1.4 + (4.8 – 1.4) * ((1.6 - 1) / (2 - 1)) = 3.44
如果你熟练那么无所谓,不然还是列三个公式一步一步来,不过这个写的也挺爽。
-
-
彩色变换
-
这里掌握HSI模型,需要注意的是:
- 色调(Hue):描述了颜色的类型,如红色、黄色、蓝色等
- 饱和度(Saturation):描述了颜色的纯度,饱和度越高,颜色越鲜艳。
- 亮度(Intensity):描述了颜色的亮度或明暗程度。
至于颜色模型是什么分量变换,,,如果只是颜色模型之间的变换例如RGB转HIS那么应该所有分量R、G、B三个分量都进行了变换;所以可能理解有误,如果可能,应该是强调图像融合的时候,若我们使用HSI变换,对于高分辨率单波段影像和低分辨率多波段影像,我们先将多波段影像的RGB转化为HIS模型,然后将I(亮度)分量换成高分辨率影像的波段,然后再进行HIS逆变换,如此得到高分辨率的多波段影像。所以这里可能指代这个I分量。
-
图像滤波
图像通过滤波和卷积进行图像增强;
-
-
对比度计算
-
考试使用四邻域计算;掌握以下即可。

-
-
辐射增强-直方图匹配(直方图规定化)和直方图均衡化
-
什么时候用直方图匹配,什么时候使用直方图均衡化,使用条件是什么?
-
-
-
是什么
-
-
首先,需要明白,直方图匹配、直方图均衡化是什么,干什么用?
我们知道,他们是用于图像的辐射增强,但是,怎么增强的?
实际上就是旧的灰度值映射到新的灰度值上,像我们之前学习的线性变换、分段线性变换、对数变换、指数变换均是如此。
而对于直方图均衡化,我们是将各个灰度值的频数均匀分配:

而直方图规定化则是将其与另一幅图象的直方图匹配(与其形状一致)或具有一种预先规定的函数形状。
简而言之,直方图均衡化是将影像直方图分布均匀化的方法;而直方图规定化是将一幅影像与另一影像的直方图匹配使二者直方图形状几乎一致的方法(也称直方图匹配)。
-
-
-
使用条件
-
-
直方图均衡化通常用于当图像的对比度较低,或者某一部分的像素值集中在较小范围内时。直方图均衡化通过拉伸像素值范围,使得每一个可能的像素值都能得到有效利用,从而提高对比度和细节可见度。
而直方图规定化通常用于当需要将一幅图像的灰度分布调整成与另一幅图像相似的情况,如在遥感影像融合、影像拼接、影像色彩校正等任务中。直方图匹配通过调整像素值的分布,使得两幅图像在视觉上具有相似的色彩和亮度特性。
-
-
小知识点
-
- 滤波可以在空间域或者频率域进行;
- 滤波的作用是平滑去噪和边缘增强
-
-
空间域中的平滑去噪-中值滤波+均值滤波的计算
-
-
我找一张很形象的动图(一幅影像一个卷积核或者说算子,下方一共8个波段对应8个卷积核):
但是需要注意的是,上方的计算并没有考虑边缘部分的计算,以下我们以一个例题进行计算。
假定一幅一影像栅格矩阵如下:
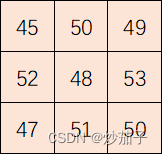
由于我们需要考虑边缘部分,因此扩充补零:

我们均值计算的卷积核或者说算子如下:

那么对于第一行第一列的数值,我们的计算如下:

所以对于中心像元45应该替换为11.1111,对于其它像元均是如此计算。需要注意的是,并不是每一个均值计算都是计算中心像元的3✖3窗内所有像元值的和再除以9(常规均值的求取);一方面要注意窗口的大小,另一方面需要注意卷积核的样子,均值计算的卷积核不止一种。
对于中值运算同样如此,但是一般不需要实际数值的卷积核,因为中值实际上就是将窗口内的数值由大到小排列取中间的数值替换中心像元的数值,但是需要注意它的窗口,不仅仅是窗口大小,更有窗口形状的变换,例如1×3的卷积核,由于计算类似,细看 。
例如下方对于中心像元的中值滤波(滤波窗口为3×3):

-
-
-
边缘增强
-
-
简单看看各种边缘增强的卷积核或者算子的样式:


样式就是卷积核内数值相加必等于0,且具有一定突出效果。
边缘增强的卷积核的作用就是突出图像中的地物边缘、轮廓线或者线状目标,提高了边缘与周围像素之间的反差。
平滑滤波就是我们说的低通滤波,边缘增强也就是我们说的高通滤波;
低通滤波顾名思义就是低的可以通过,具体指代的是低频部分可以通过,但是这里的低频部分一般指代图像的平滑和均匀部分,因为这部分区域的像素变化较慢或者变化较小;è常用于图像平滑和噪声去除。
而高通滤波顾名思义就是高的可以通过,具体指代的是高频部分可以通过,这里的高频成分一般指代图像的边缘和细节部分,因为这部分区域像素值变化较快或者变化较大。è常用于图像锐化和边缘检测。
对频率域来说,通过傅里叶变换将空间域变换到频率域,然后在频率域上进行高通滤波和低通滤波,需要特别注意的是,哪个是在频率域中中间位哪个是在边缘位置上进行滤波;
由于我们的拿到的影像一般如下(经过频谱居中):

中间部分亮只是因为它的能量比较多,也就是说影像中大部分区域都是低频部分也就是比较平滑。
我们进行低通滤波实际上对频谱图像中心的区域进行处理(让中间区域通过),而抑制或消除边缘部分。
而高通滤波则是对边缘部分进行处理。
-
图像分割和图像分类
首先说说图像分割是什么,了解一下,直接摘了:
一幅图象通常是由代表物体的图案与背景组成,简称物体与背景。若想从一幅图象中“提取”物体,可以设法用专门的方法标出属于该物体的点,如把物体上的点标为“1”,而把背景点标为“0”,通过分割以后,可得一幅二值图象。
-
-
图像分割的作用
-
将一个图像分割成若干个具有特定意义的区域,这些区域通常具有一致的某种属性,如颜色、亮度或纹理等。
-
-
图像分割的计算方法
-
-
灰度阈值法
当影像直方图具有两个峰,分别与两个灰度级范围相对应 ,我们可以将分割阈值设置于两峰之间的谷底,这样能够将目标物和背景分割。它适用于目标在其内部具有均匀一致的灰度值并分布在另一个灰度值均匀的背景时。
或者说,图像中的不同区域在直方图上有不同的峰值。它适用于图像的直方图具有明显的多峰特性,且不同峰值对应的像素值具有明显的区分度也即相邻两峰间的谷对应于目标边缘附近有相对较少数目的点时。
-
梯度方法
梯度方法是基于图像的边缘信息来进行图像分割,它适用于图像中的目标区域和背景之间具有明显的边缘界限。
-
区域方法
类似种子扩散算法,要求像素间具有一定的连通性和邻近性,实际上就是需要有一定的相似度
-
数学形态学方法
多用于二值化图像(例如在对分类或者分割好的影像进行腐蚀膨胀去除小斑块孤岛问题等),当然灰度图像也是可以的。
-
-
遥感影像的地物分类,如何判断特征空间分成几类地物?
-
看图说话:

但实际上我们是通过距离(例如曼哈顿距离、欧式距离等)、相关系数、最大似然法等进行地物判断。
-
- 精度评价方法及其计算?
总体精度(Overall Accuracy):这是分类结果正确的样本所占的比例。它表示了整体分类的准确性,但不能反映各类别间的精度差异。
制图精度(Producer's Accuracy):也被称为“用户精度”,是一种针对每个类别的精度度量,它表示了被正确分类到该类别的样本所占该类别所有样本的比例。
漏分误差(Omission Error):对某一类别,它是未被正确分类到该类别的样本所占该类别所有样本的比例,是制图精度的补。
错分误差(Commission Error):对某一类别,它是被错误分类到该类别的样本所占所有被分类到该类别的样本的比例。
混淆矩阵(Confusion Matrix):它是一个表格,用于描述分类结果的详细情况。行代表实际类别,列代表预测类别,表格中的元素表示各类别之间的样本数量。
Kappa系数(Kappa Coefficient):Kappa系数是一种用于一种测定模型分类结果与实际影像吻合度或精度的统计量。值越接近1,表示分类结果越好;值为0表示预测分类结果与随机结果无差异;值小于0表示分类结果比随机结果还差。
-
-
- 混淆矩阵
-
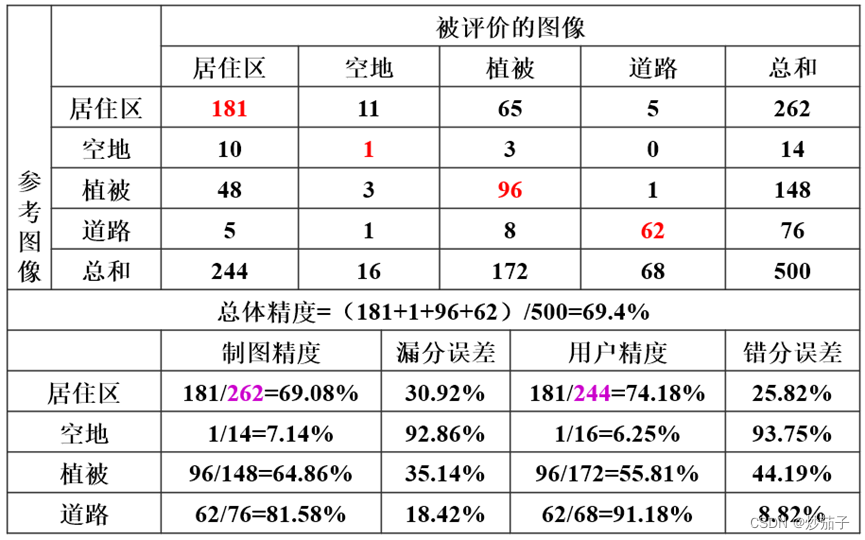
-
-
-
Kappa系数
-
-



-
-
监督分类和非监督分类的常见算法及其特征
-
监督分类
-
-
- 最小距离分类器
- 最大似然分类器
- 神经网络分类器
- 决策树分类器
- 支持向量机分类器
- 随机森林分类器
特征:地物类型是确定的,有充足的参照数据作为训练样本,从训练样本得到解译标志,并用于训练分类器以将光谱数据分类制成专题图。
-
-
-
非监督分类
-
-
- K-均值算法(K-mean)
- ISODATA算法(动态聚类法)
特征:使用基于聚类的算法,根据图像内在包含的统计信息将光谱图像划分成许多光谱类别,没有预先定义好的类,分析人员负责将各个光谱类别标明和合并为有意义的类别。
监督分类有哪几种常见算法?非监督分类又有哪几种常见算法?特征是什么,适用于什么样的分类条件;
-
-
分类结果的改善
-
- 扩大样本数量;
- 剔除不纯净的样本;
- 选用不同的分类算法和相关参数;
- 影像的分辨率提升以及影像的预处理例如辐射定标、大气校正等;
- 了解地物分类的特征,尝试增加更多特征,例如对于植被使用NDVI、NDWI等;
对于不同地物的样本,我们可以对其进行分离度分析来查看各类样本的可分离性,若较为模糊就应该对样本进行改进处理;对于分类效果好坏通过前文的精度评价中各项指标进行。
-
遥感数字图像处理课程包含了哪几块的内容(思考题)
- 遥感数字图像处理的发展史
- 遥感数字图像的获取、查询和检索、统计和特征、数据格式和存储方式、显示和拉伸
- 图像的辐射校正和几何校正(辐射校正又包括系统辐射校正、辐射定标、大气校正和地形辐射校正;而几何校正又包括正射校正、几何粗校正和几何精校正;)
- 图像的增强(包括各种变换例如傅里叶变换、K-L变换、K-T变换,以及他们和卷积滤波的结合包括平滑去噪和边缘增强两个方面)
- 图像的分割和分类(分割包括各种分割算法例如灰度阈值法、数学形态学算法等;分类包括监督分类和非监督分类算法,具体又有随机森林支持向量机等、ISODATA和K均值等)