目录
- 1.刚体状态的表达
- 2.顺向运动学及DH表
- 3.逆向运动学
1.刚体状态的表达
我们前面已经学习了刚体移动和转动的表达,那么怎么将两者在数学上结合呢?这里我们开始构造如下矩阵,记作:
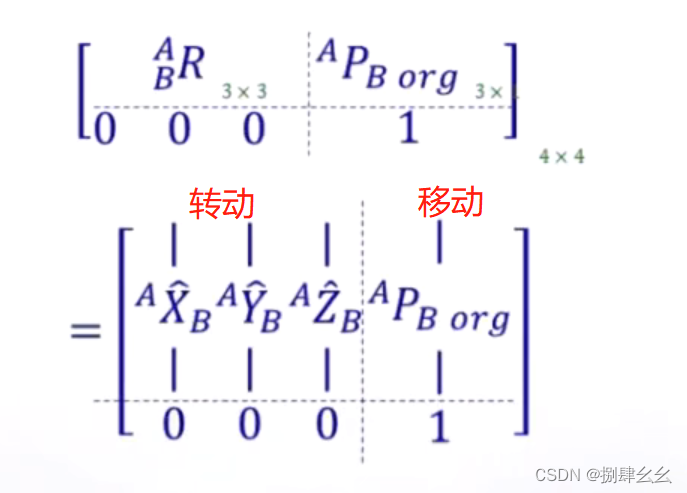
下面我们来看一下只有移动情况下的刚体的描述:
- 采用向量表达式,可得如下公式,具体向量图亦如下:
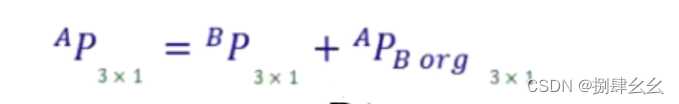
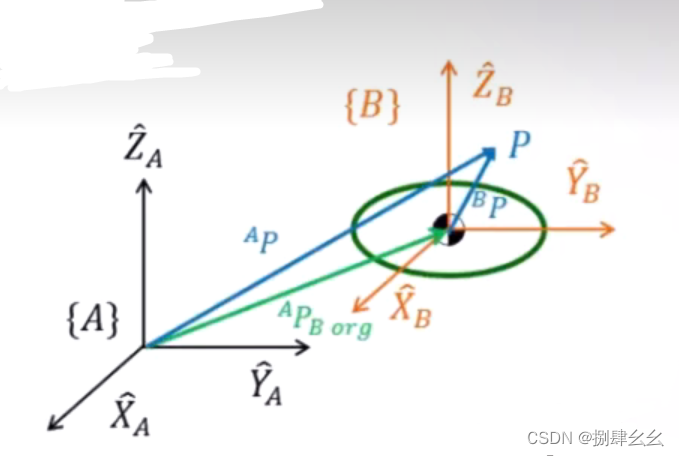
最后得出:
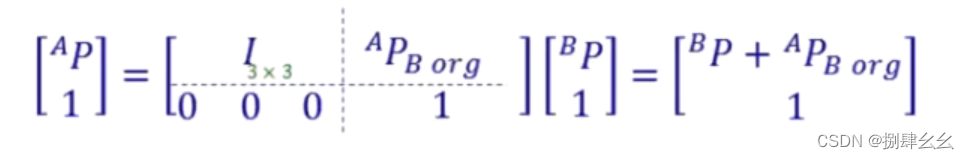
接着我们来看一下只有转动情况下的刚体的描述:
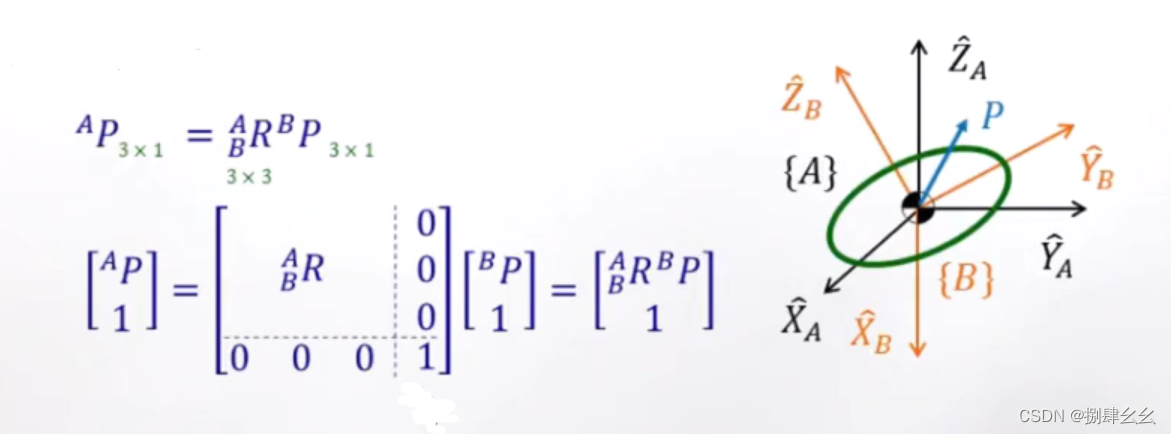
同理我们来看一下只有复合情况下的刚体的描述:

2.顺向运动学及DH表
-
运动学:讨论运动状态本身,没有考虑到产生运动的力(位移、速度、加速度、时间之间的关系)
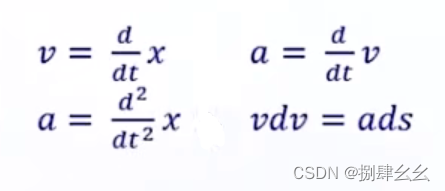
-
动力学:什么样的力造成什么样的运动 (力、力矩)
①牛顿第二定理
②功能守恒 -
顺向运动学(FK):以机械手为例,末端的状态Wp为输出,每个关节的转角Θ为变量,可得到顺向的函数式
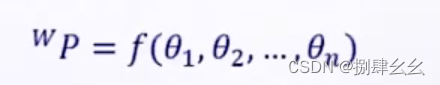
-
串联杆件之间的位置描述:需要4个参数才能确定两个转轴直接的空间关系
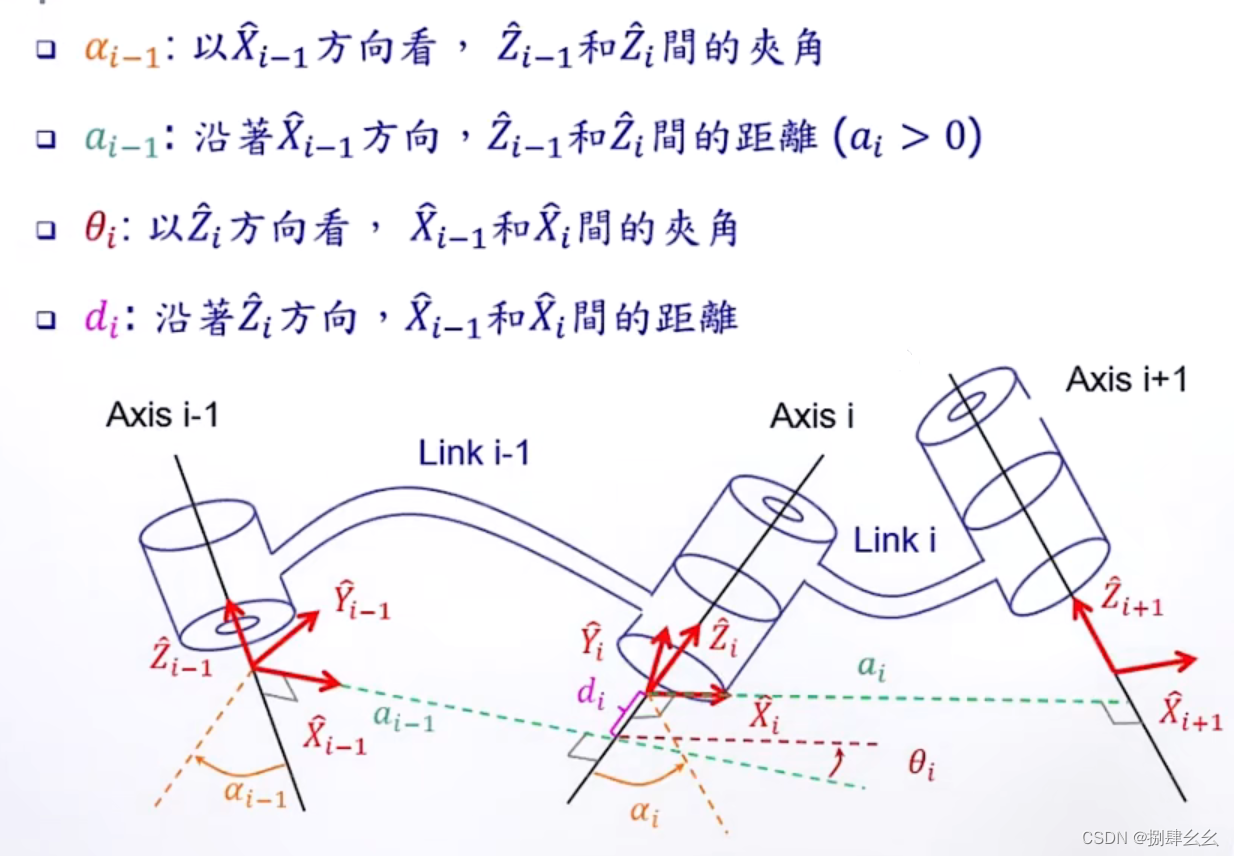
-
利用前面学的刚体转动和移动的,将两轴之间的转动 矩阵推出(四步旋转移动得到)
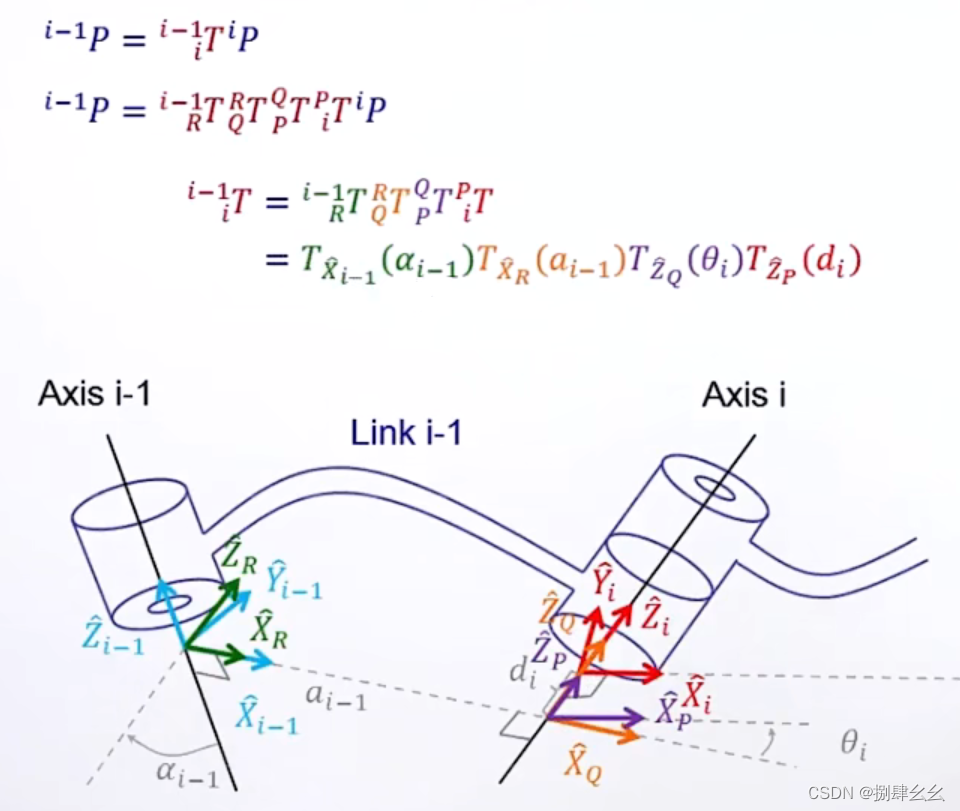
-
做个例题来感受一下:
frames0就是地杆 n是末端
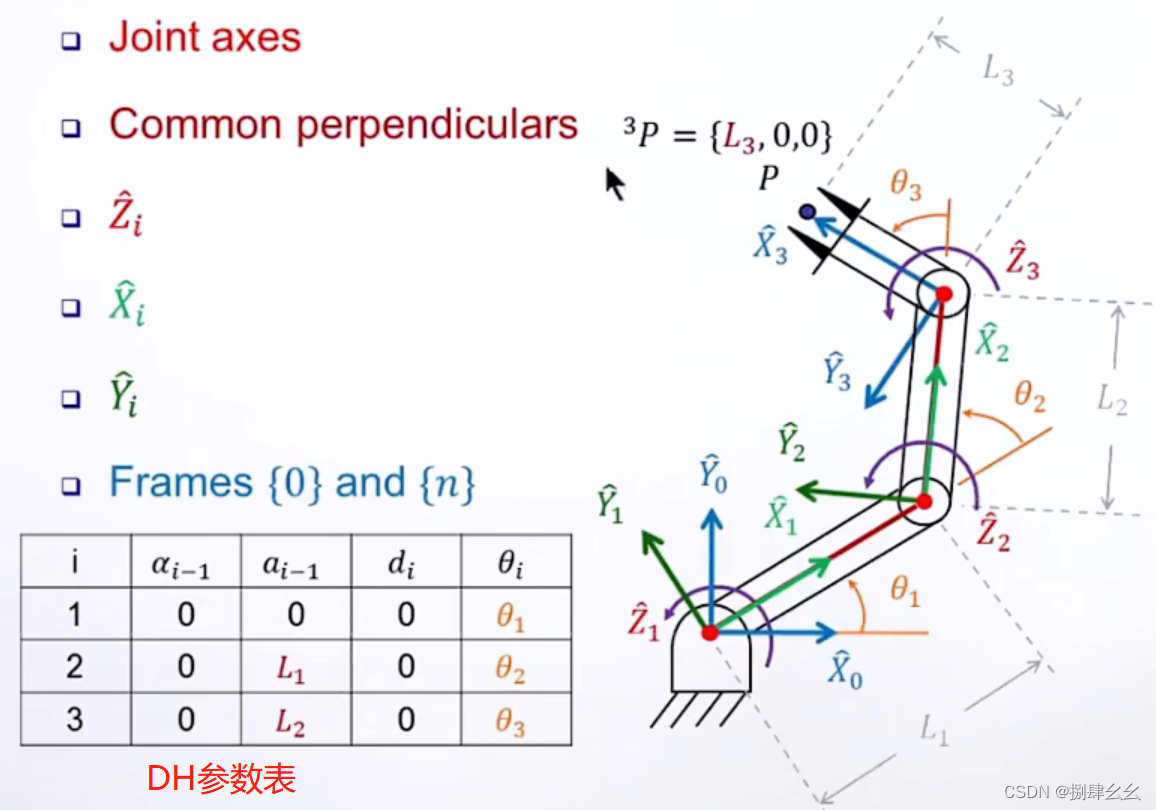
3.逆向运动学
- 和上面所说的顺向相反,通过末端点的状态来反算所需要转动的Θi对应的所有角度
- 求解方法:
对于变换矩阵,左上的33是旋转变化,其中有限制是①XYZ长度为1②XYZ两两垂直(6个限制、6个自由度)
右上方的31表示相对于原点的位移 ,有3个自由度
总结就是:12个方程式、6个未知数以及6个限制条件

- 不同解:①可以到达点的集合②任意到达点的集合


- 解的数目:和DH参数中的a有关,当轴数为6时,解的数目如下

- 具体求解方法:
①几何法
②代数法
(具体略)