( “树” 之 DFS) 617. 合并二叉树 —

( “树” 之 DFS) 617. 合并二叉树 ——【Leetcode每日一题】

news/2024/11/24 13:49:05/

617. 合并二叉树

给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

示例 1：

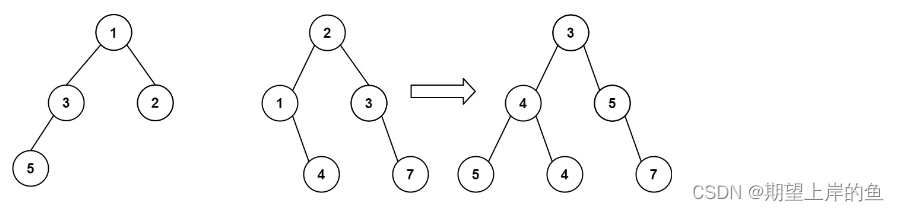
在这里插入图片描述

输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]

示例 2：

输入：root1 = [1], root2 = [1,2]
输出：[2,2]

提示：

两棵树中的节点数目在范围 [0, 2000] 内
$10^4 <= Node.val <= 10^4$

思路：递归 DFS

1、首先要清楚我们要写的递归函数返回什么？

这里的mergeTrees返回合并后的头结点；

2、然后考虑边界，就是什么时候返回return，以及是否需要合并：

如果root1和root2中有一个节点为空，则不需要合并，直接另外一个节点即可；
如果都不空，则需要合并，可以将root2合并到root1，不用再申请新的节点；
当前节点处理完，在递归处理左子树和右子树；
返回合并后的头结点root1.

代码：(Java、C++)

Java

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {if(root1 == null) return root2;if(root2 == null) return root1;root1.val += root2.val;root1.left = mergeTrees(root1.left, root2.left);root1.right = mergeTrees(root1.right, root2.right);return root1;}
}

C++

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {if(root1 == NULL) return root2;if(root2 == NULL) return root1;root1->val += root2->val;root1->left = mergeTrees(root1->left, root2->left);root1->right = mergeTrees(root1->right, root2->right);return root1;}
};

运行结果：

在这里插入图片描述

复杂度分析：

时间复杂度： $O (min (m, n))$ ，其中 m和 n 分别是两个二叉树的节点个数。对两个二叉树同时进行深度优先搜索，只有当两个二叉树中的对应节点都不为空时才会对该节点进行显性合并操作，因此被访问到的节点数不会超过较小的二叉树的节点数。
空间复杂度： $O (min (m, n))$ ，其中 m和 n 分别是两个二叉树的节点个数。空间复杂度取决于递归调用的层数，递归调用的层数不会超过较小的二叉树的最大高度，最坏情况下，二叉树的高度等于节点数。