一.聚类算法的简介

        对于"监督学习"(supervised learning)，其训练样本是带有标记信息的，并且监督学习的目的是：对带有标记的数据集进行模型学习，从而便于对新的样本进行分类。而在“无监督学习”(unsupervised learning)中，训练样本的标记信息是未知的，目标是通过对无标记训练样本的学习来揭示数据的内在性质及规律，为进一步的数据分析提供基础。对于无监督学习，应用最广的便是"聚类"(clustering)。
        "聚类算法"试图将数据集中的样本划分为若干个通常是不相交的子集，每个子集称为一个“簇”(cluster)，通过这样的划分，每个簇可能对应于一些潜在的概念或类别。
        我们可以通过下面这个图来理解：

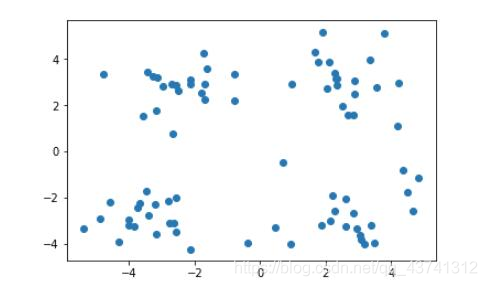
        上图是未做标记的样本集，通过他们的分布，我们很容易对上图中的样本做出以下几种划分。
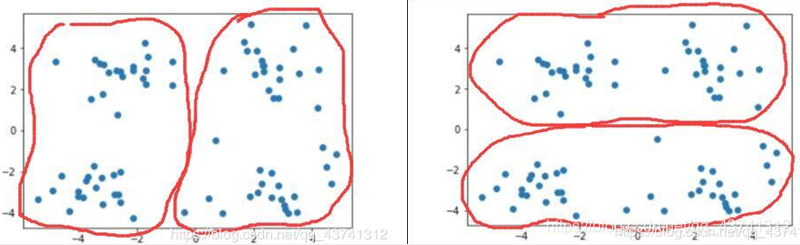
                当需要将其划分为两个簇时，即 k=2时：

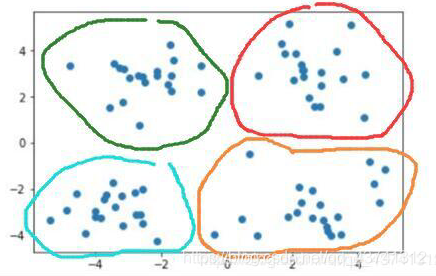
        当需要将其划分为四个簇时，即 k=4 时：

二.K-means聚类算法

        kmeans算法又名k均值算法,K-means算法中的k表示的是聚类为k个簇，means代表取每一个聚类中数据值的均值作为该簇的中心，或者称为质心，即用每一个的类的质心对该簇进行描述。
        其算法思想大致为：先从样本集中随机选取 k个样本作为簇中心，并计算所有样本与这 k个“簇中心”的距离，对于每一个样本，将其划分到与其距离最近的“簇中心”所在的簇中，对于新的簇计算各个簇的新的“簇中心”。
        根据以上描述，我们大致可以猜测到实现kmeans算法的主要四点：
          （1）簇个数 k 的选择
          （2）各个样本点到“簇中心”的距离
          （3）根据新划分的簇，更新“簇中心”
          （4）重复上述2、3过程，直至"簇中心"没有移动
        优缺点：

• 优点：容易实现
• 缺点：可能收敛到局部最小值，在大规模数据上收敛较慢

三.K-means算法步骤详解

Step1.K值的选择

k 的选择一般是按照实际需求进行决定，或在实现算法时直接给定 k 值。

说明：
A.质心数量由用户给出，记为k，k-means最终得到的簇数量也是k
B.后来每次更新的质心的个数都和初始k值相等
C.k-means最后聚类的簇个数和用户指定的质心个数相等，一个质心对应一个簇，每个样本只聚类到一个簇里面
D.初始簇为空

Step2.距离度量

        将对象点分到距离聚类中心最近的那个簇中需要最近邻的度量策略，在欧式空间中采用的是欧式距离，在处理文档中采用的是余弦相似度函数，有时候也采用曼哈顿距离作为度量，不同的情况实用的度量公式是不同的。

2.1.欧式距离

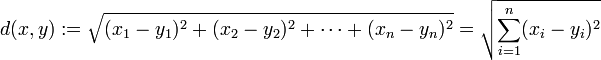
2.2.曼哈顿距离

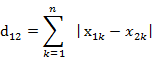
2.3.余弦相似度

        A与B表示向量(x1,y1)，(x2,y2)
        分子为A与B的点乘，分母为二者各自的L2相乘，即将所有维度值的平方相加后开方。

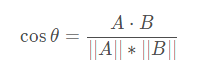
说明：
A.经过step2，得到k个新的簇，每个样本都被分到k个簇中的某一个簇
B.得到k个新的簇后，当前的质心就会失效，需要计算每个新簇的自己的新质心

Step3.新质心的计算

        对于分类后的产生的k个簇，分别计算到簇内其他点距离均值最小的点作为质心（对于拥有坐标的簇可以计算每个簇坐标的均值作为质心）

说明：
A.比如一个新簇有3个样本：[[1,4], [2,5], [3,6]]，得到此簇的新质心=[(1+2+3)/3, (4+5+6)/3]
B.经过step3，会得到k个新的质心，作为step2中使用的质心

Step4.是否停止K-means

        质心不再改变，或给定loop最大次数loopLimit

说明：
A当每个簇的质心，不再改变时就可以停止k-menas
B.当loop次数超过looLimit时，停止k-means
C.只需要满足两者的其中一个条件，就可以停止k-means
C.如果Step4没有结束k-means，就再执行step2-step3-step4
D.如果Step4结束了k-means，则就打印(或绘制)簇以及质心

四.python实现+代码详解

        以下是python得实例代码以及代码的详解，应该可以理解的。

import random
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt# 计算欧拉距离
def calcDis(dataSet, centroids, k):clalist=[]for data in dataSet:diff = np.tile(data, (k, 1)) - centroids  #相减   (np.tile(a,(2,1))就是把a先沿x轴复制1倍，即没有复制，仍然是 [0,1,2]。 再把结果沿y方向复制2倍得到array([[0,1,2],[0,1,2]]))squaredDiff = diff ** 2     #平方squaredDist = np.sum(squaredDiff, axis=1)   #和  (axis=1表示行)distance = squaredDist ** 0.5  #开根号clalist.append(distance) clalist = np.array(clalist)  #返回一个每个点到质点的距离len(dateSet)*k的数组return clalist# 计算质心
def classify(dataSet, centroids, k):# 计算样本到质心的距离clalist = calcDis(dataSet, centroids, k)# 分组并计算新的质心minDistIndices = np.argmin(clalist, axis=1)    #axis=1 表示求出每行的最小值的下标newCentroids = pd.DataFrame(dataSet).groupby(minDistIndices).mean() #DataFramte(dataSet)对DataSet分组，groupby(min)按照min进行统计分类，mean()对分类结果求均值newCentroids = newCentroids.values# 计算变化量changed = newCentroids - centroidsreturn changed, newCentroids# 使用k-means分类
def kmeans(dataSet, k):# 随机取质心centroids = random.sample(dataSet, k)# 更新质心 直到变化量全为0changed, newCentroids = classify(dataSet, centroids, k)while np.any(changed != 0):changed, newCentroids = classify(dataSet, newCentroids, k)centroids = sorted(newCentroids.tolist())   #tolist()将矩阵转换成列表 sorted()排序# 根据质心计算每个集群cluster = []clalist = calcDis(dataSet, centroids, k) #调用欧拉距离minDistIndices = np.argmin(clalist, axis=1)  for i in range(k):cluster.append([])for i, j in enumerate(minDistIndices):   #enymerate()可同时遍历索引和遍历元素cluster[j].append(dataSet[i])return centroids, cluster# 创建数据集
def createDataSet():return [[1, 1], [1, 2], [2, 1], [6, 4], [6, 3], [5, 4]]if __name__=='__main__': dataset = createDataSet()centroids, cluster = kmeans(dataset, 2)print('质心为：%s' % centroids)print('集群为：%s' % cluster)for i in range(len(dataset)):plt.scatter(dataset[i][0],dataset[i][1], marker = 'o',color = 'green', s = 40 ,label = '原始点')#  记号形状       颜色      点的大小      设置标签for j in range(len(centroids)):plt.scatter(centroids[j][0],centroids[j][1],marker='x',color='red',s=50,label='质心')plt.show()

五.K-means算法补充

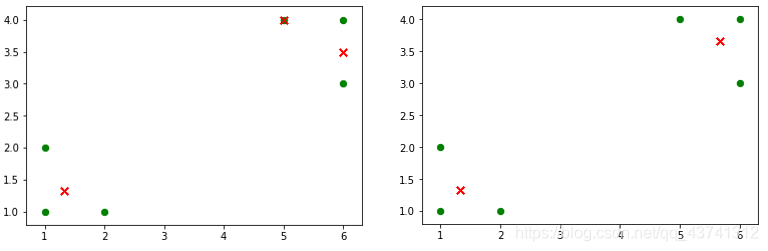
1.对初始化敏感，初始质点k给定的不同，可能会产生不同的聚类结果。如下图所示，右边是k=2的结果，这个就正好，而左图是k=3的结果，可以看到右上角得这两个簇应该是可以合并成一个簇的。

改进：
对k的选择可以先用一些算法分析数据的分布，如重心和密度等，然后选择合适的k

2.使用存在局限性，如下面这种非球状的数据分布就搞不定了：

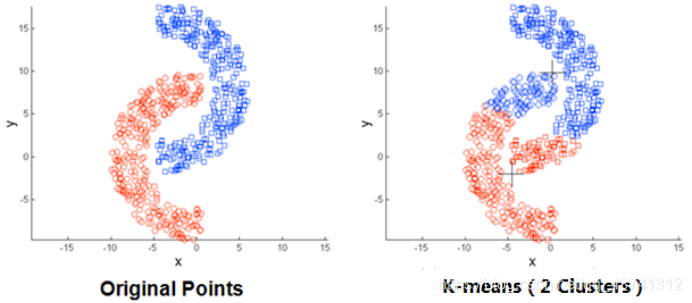
3.数据集比较大的时候，收敛会比较慢。

4.最终会收敛。不管初始点如何选择，最终都会收敛。可是是全局收敛，也可能是局部收敛。

六.小结

        1. 聚类是一种无监督的学习方法。聚类区别于分类，即事先不知道要寻找的内容，没有预先设定好的目标变量。

        2. 聚类将数据点归到多个簇中，其中相似的数据点归为同一簇，而不相似的点归为不同的簇。相似度的计算方法有很多，具体的应用选择合适的相似度计算方法

        3. K-means聚类算法，是一种广泛使用的聚类算法，其中k是需要指定的参数，即需要创建的簇的数目，K-means算法中的k个簇的质心可以通过随机的方式获得，但是这些点需要位于数据范围内。在算法中，计算每个点到质心得距离，选择距离最小的质心对应的簇作为该数据点的划分，然后再基于该分配过程后更新簇的质心。重复上述过程，直至各个簇的质心不再变化为止。

        4. K-means算法虽然有效，但是容易受到初始簇质心的情况而影响，有可能陷入局部最优解。为了解决这个问题，可以使用另外一种称为二分K-means的聚类算法。二分K-means算法首先将所有数据点分为一个簇；然后使用K-means（k=2）对其进行划分；下一次迭代时，选择使得SSE下降程度最大的簇进行划分；重复该过程，直至簇的个数达到指定的数目为止。实验表明，二分K-means算法的聚类效果要好于普通的K-means聚类算法。