牛顿法是一种用来寻找函数零点的迭代方法,它基于以下思路,如果我们知道了一个函数在某个点的切线,那么函数的零点就可以通过切线与x轴的交点来近似计算。
给定一个函数,找到零点
,过程如下:
选择初始点,然后使用这个点处的切线来近似
,也就是说,找到下面这条直线:
这样,我们可以通过将其与x轴相交一获得更接近真实零点的新估计值:
从上式可以看出,如果我们对一次,则可以计算出一个更好的估计值
,然后我们可以不断重复此过程,直到达到我们满意的精度或次数为止。
下面举例说明:
用牛顿法求解一元二次方程,程序比较简单,利用导函数与横轴的交点的横坐标不断迭代即可,程序清单如下:
#include <stdio.h>
#include <stdlib.h>
#include <math.h>//newton methond to get the root of
//equation of two degree f(x) = x^2-8x+9
//the deritive is f'(x) = 2x - 8;
static void newton_methed(void)
{// init value of start point. double x1 = 8.0, x2=0.0, y1, root;double k; // the gradient of f(x)while(fabs(x1-x2) > 1e-6) {x2=x1;k = 2 * x1 - 8;y1 = x1*x1 - 8*x1 + 9;root = (-1 * y1)/k + x1; //according y-y1=k(x-x1)x1 = root;printf("root is %f.\n", root);}return;
}int main(void)
{newton_methed();return 0;
}图解说明:
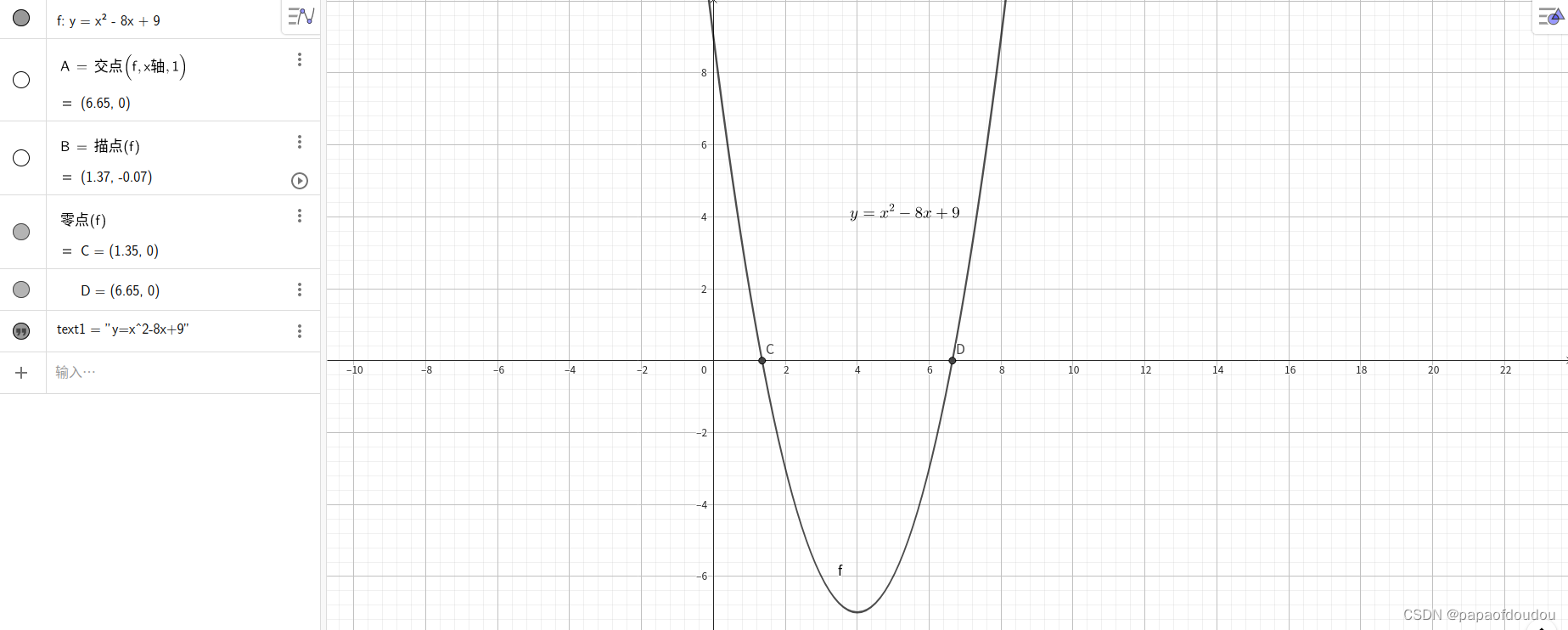
下图展示了迭代过程:
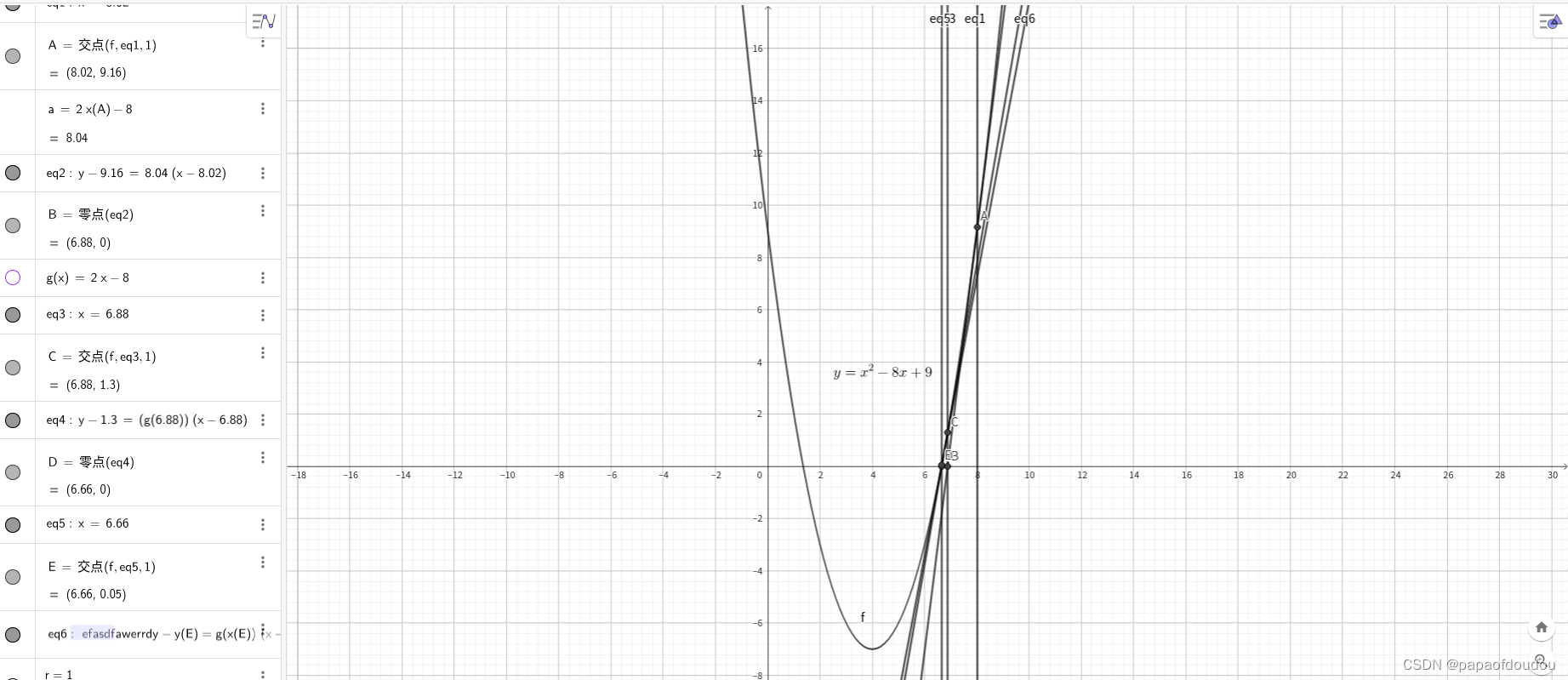
根值到了极度接近的阶段,宏观上已经看不出切线和坐标轴的交点,即便放大绘图,也会感受到工具渲染非常的吃力。下图展示了三次迭代后的效果,左边是原函数和坐标轴的交点,邮编是三伦迭代的切线和X轴的交点,可以看到,交点非常的接近了。

如果将迭代初始值甚至为一元二次函数的极点位置,程序将失效,原因是此时极点的切线位置和X轴平行,没有交点,算法无法执行下去。
对于这个例子来说,如果将初始的X1设置为4,算法将会输出非法值。

但是只要打破平衡,稍微偏离极点中心哪怕一点点,算法将给出正确的值,如果向左偏离,则得到左交点,如果向右偏离,将得到右交点,结合图形,很容易理解这些结论。




计算左边根的迭代示意图
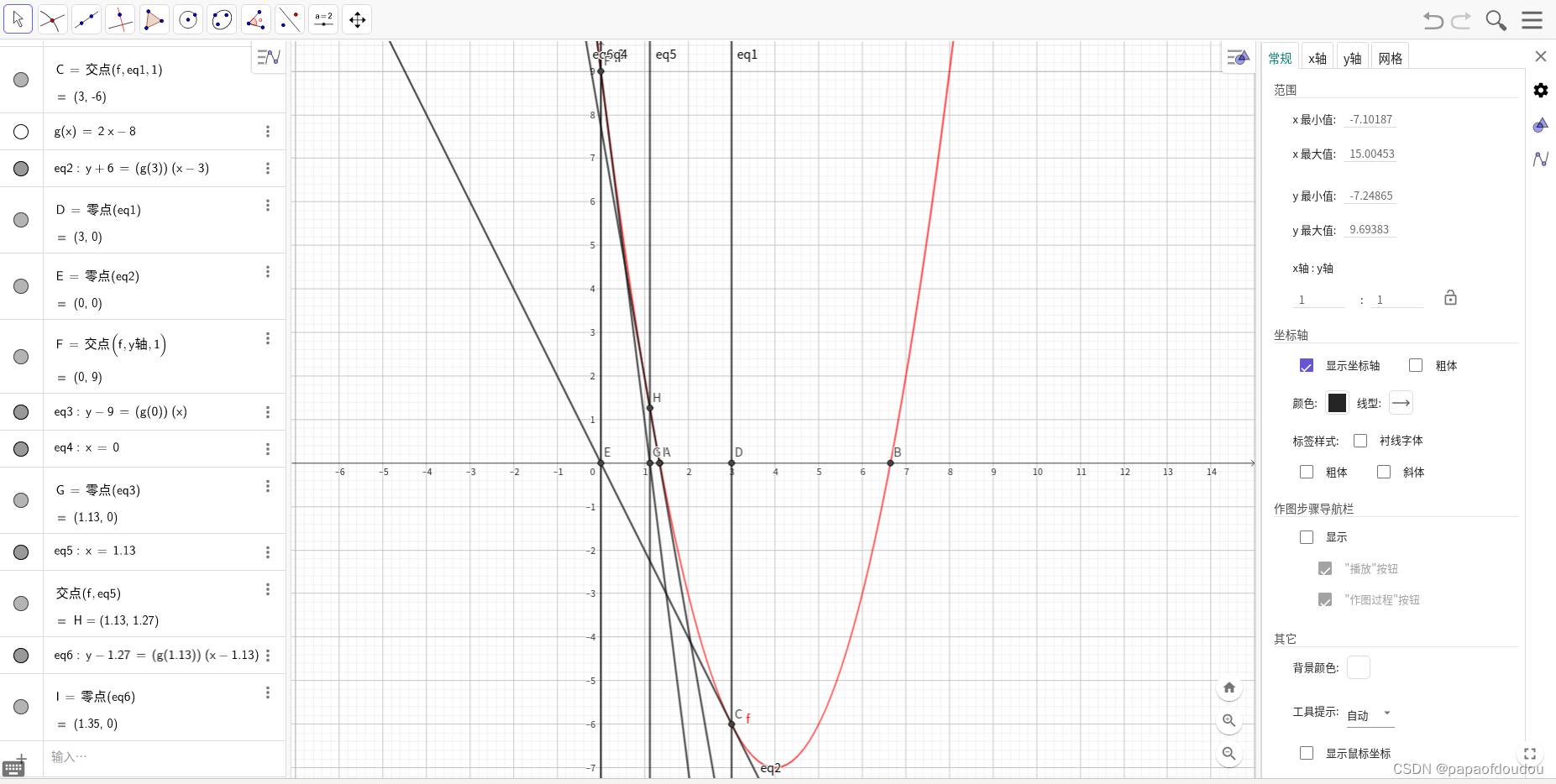
一个不算简单的解方程问题,数形结合起来后,直观了很多,看来数学从高的观点往下看,往往会更有收获。
一个新的例子,自然对数求根:
geogebra得到的两个根是+/- 1.41.
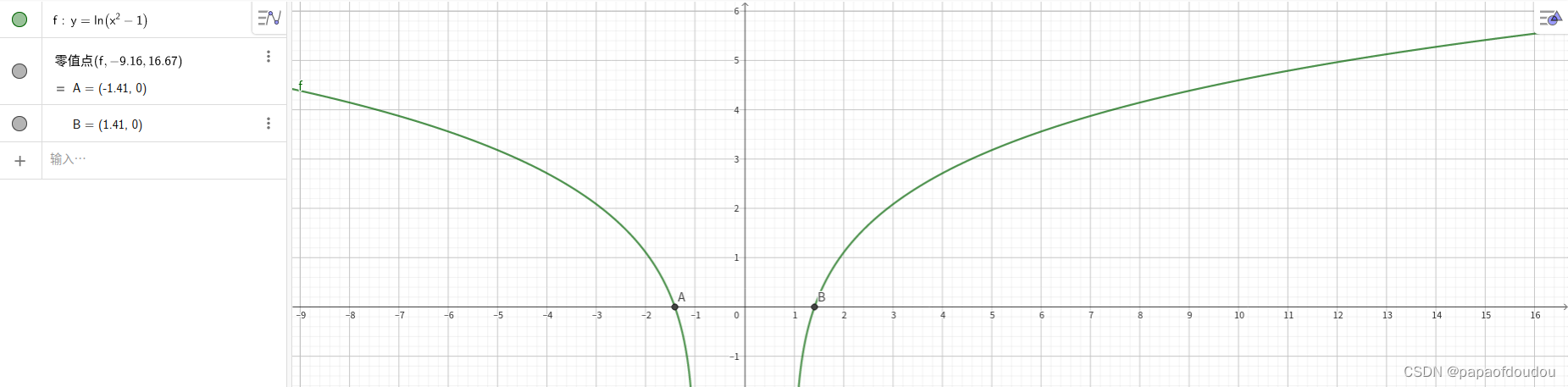
程序:
#include <stdio.h>
#include <stdlib.h>
#include <math.h>//newton methond to get the root of
//equation of two degree f(x) = x^2-8x+9
//the deritive is f'(x) = 2x - 8;
static void newton_methed1(void)
{// init value of start point. double x1 = 3.99999999, x2=0.0, y1, root;double k; // the gradient of f(x)while(fabs(x1-x2) > 1e-6) {x2=x1;k = 2 * x1 - 8;y1 = x1*x1 - 8*x1 + 9;root = (-1 * y1)/k + x1; //according y-y1=k(x-x1)x1 = root;printf("root is %f.\n", root);}return;
}//newton methond to get the root of
//equation of two degree f(x) = log(x^2-1)
//the deritive is f'(x) = 2x/(x^2-1);
static void newton_methed2(float x1)
{// init value of start point. double x2=0.0, y1, root;double k; // the gradient of f(x)while(fabs(x1-x2) > 1e-6) {x2=x1;k = 2 * x1/(x1*x1 - 1);y1 = log(x1*x1-1);root = (-1 * y1)/k + x1; //according y-y1=k(x-x1)x1 = root;printf("root is %f.\n", root);}return;
}int main(void)
{//newton_methed1();newton_methed2(3.999999999);newton_methed2(-3.999999999);return 0;
}程序迭代过程,最终得到了正确的根:

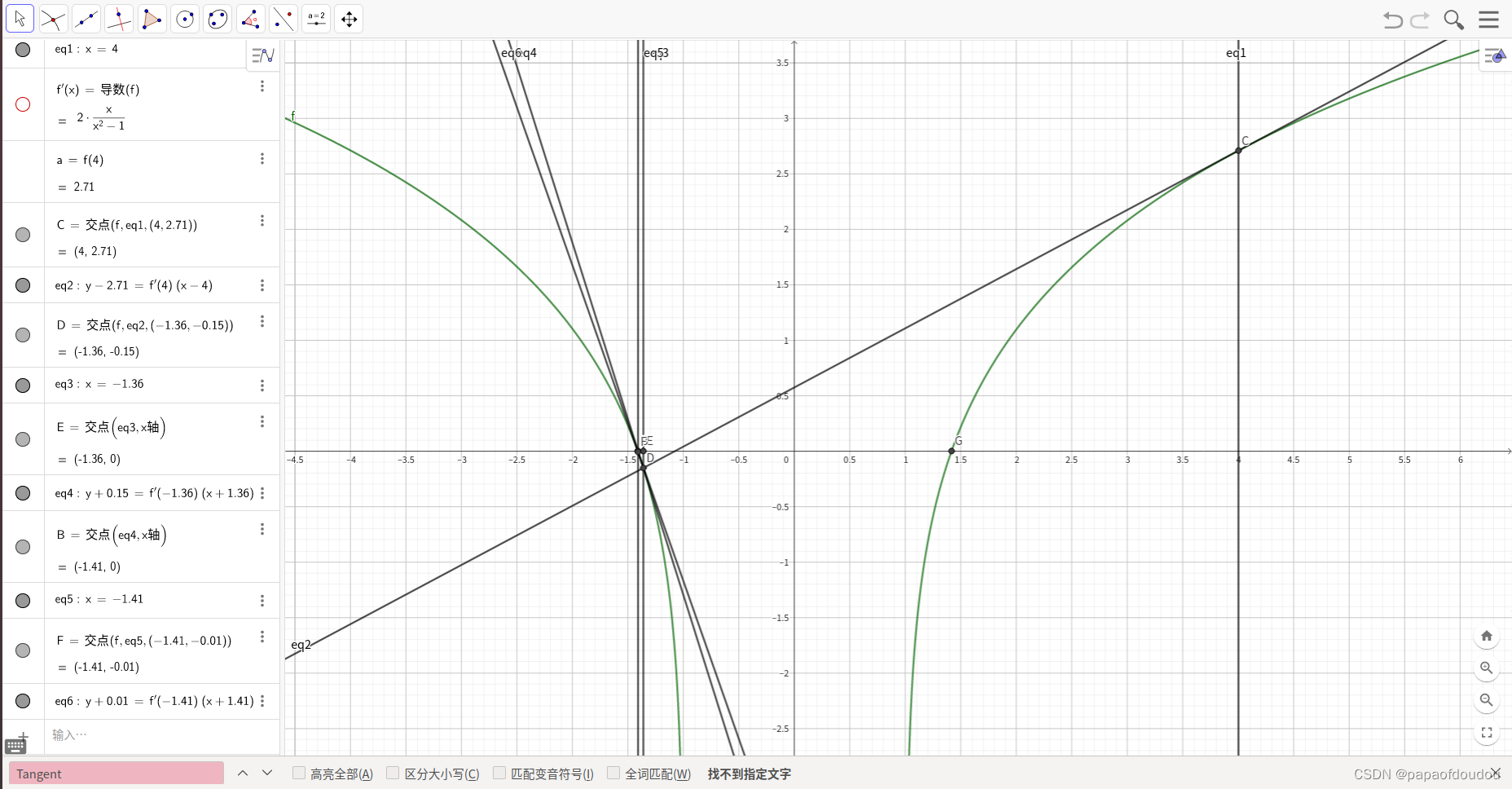
迭代数次后的逼近位置:
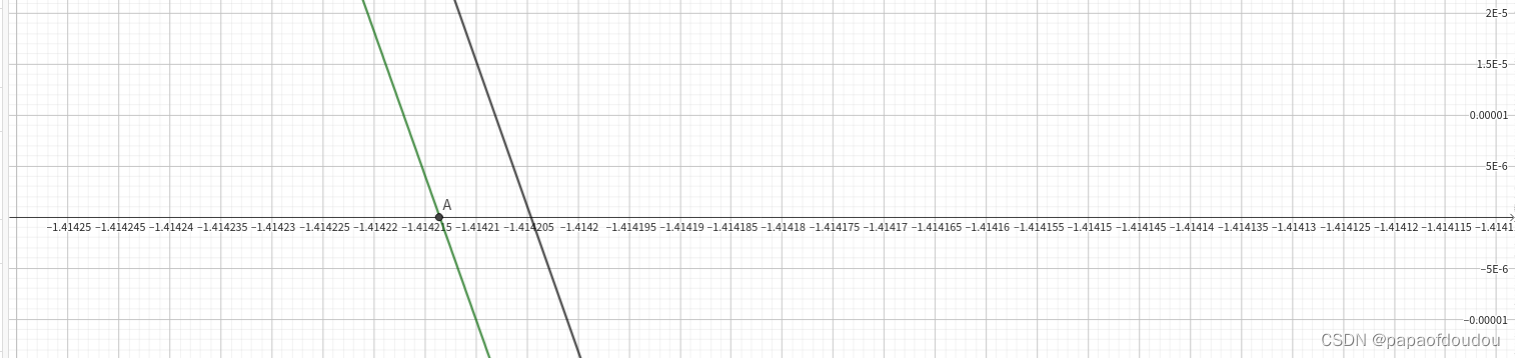
总结:
牛顿法的主要优点是,它在每次迭代中都收敛的非常快,在实践中被证明比其他迭代方法更快,但是它也有缺点,就像例子中看到的,当函数具有多个局部零点时,算法的初始值可能导致收敛到错误的根。
解方程是一种近似数学,虽然有的时候能够获得方程的解析式,但大多数的时候(5次及以上的普通方程)是没有解析式的,这个时候只能通过数值解法得到近似解。即便对于有解析式可解方程,通常根也是无理数,没有精确解,所以解方程实际上是一件“差不多”就可以的事,所以计算机能够很好的胜任这份工作。