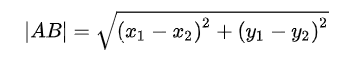欧拉回路

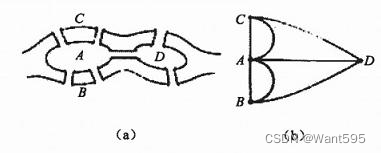
有一条名为Pregel的河流经过Konigsberg城。城中有7座桥，把河中的两个岛与河岸连接起来。当地居民热衷于一个难题：是否存在一条路线，可以不重复地走遍7座桥。这就是著名的七桥问题。它由大数学家欧拉首先提出，并给出了完美的解答，如图所示。

欧拉首先把图(a)中的七桥问题用图论的语言改写成图(b)，则问题变成了：能否从无向图中的一个结点出发走出一条道路，每条边恰好经过一次。这样的路线称为欧拉道路（enlerian path），可以形象地称为“一笔画”。
不难发现，在欧拉道路中，“进”和“出”是对应的——除了起点和终点外，其他点的“进出”次数应该相等，换句话说，除了起点和终点外，其他点的度数应该有偶数。很可惜，在七桥问题中，所有4个点的度数均是奇数（这样的点也称为奇点），因此不可能存在欧拉道路。上述条件也是充分条件——如果一个无向图是连通的，且最多只有两上奇点，则一定存在欧拉道路。如果有两个奇点，则必须从其中一个奇点出发，另一个奇点终止；如果奇点不存在，则可以从任意点出发，最终一定会回到该点（称为欧拉回路）。