今天是个好日子,要搞栈的实验
没啥就是链栈和顺序栈
和出栈入栈,强大都是从最基本开始的
来和我一起写写吧
//顺序栈
typedef struct node{int *base;int *top;int sizer;
}shed;//链栈
typedef struct Node{
int data;
struct Node* next;
}*stact,link;
//顺序栈的初始化基本的模板
接下来就是push和pop
//顺序栈的入栈
void push(shed &s,int e){if((s.top-s.base)!=s.sizer)*(s.top++)=e;elseprintf("栈满,操作无效");
}//链栈的入栈
void pushs(stact &t,int i){stact k=(stact)malloc(sizeof(stact));k->next=t->next;k->data=i;t->next=k;}一点不长但是就是脑袋要清晰一点 ,错了就要每个看一遍难受的要命
pop
//顺序栈的出栈
void pop(shed &s,int &a){if(s.base==s.top)printf("栈空操作无效");elsea=*(--s.top);
}//链表的出栈
void pops(stact t,int &e){if(t->next!=NULL){stact p=t->next;t->next=p->next;//头节点后第一个出去的e=p->data;free(p);}
}细心永远不亏!!
接下来就是遍历输出
//链栈的展示
void shows(stact t){
stact p=t->next;
while(p!=NULL){printf("%d ",p->data);p=p->next;
}
printf("\n");
}//顺序栈的输出展示
void show(shed &s){int* j=s.base;for(;j<s.top;j++)printf("%d ",*j);printf("\n");
}没有写返回栈元素数目(实验的没要求)
其他的要求都可以用这上面的函数拼成
写完有时间看看我测试没写完的题目了
FBI树
Description
我们可以把由“0”和“1”组成的字符串分为三类:全“0”串称为B串,全“1”串称为I串,既含“0”又含“1”的串则称为F串。
FBI树是一种二叉树,它的结点类型也包括F结点,B结点和I结点三种。由一个长度为2^N的“01”串S可以构造出一棵FBI树T,递归的构造方法如下:
1)T的根结点为R,其类型与串S的类型相同;
2)若串S的长度大于1,将串S从中间分开,分为等长的左右子串S1和S2;由左子串S1构造R的左子树T1,由右子串S2构造R的右子树T2。
现在给定一个长度为2^n的“01”串,请用上述构造方法构造出一棵FBI树,并输出它的后序遍历序列。
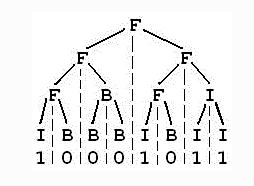
Input
第一行是一个整数N(0 < = N < = 10),第二行是一个长度为2^N的“01”串。
数据规模和约定,对于全部的数据,N < = 10。
注:
[1] 二叉树:二叉树是结点的有限集合,这个集合或为空集,或由一个根结点和两棵不相交的二叉树组成。这两棵不相交的二叉树分别称为这个根结点的左子树和右子树。
[2] 后序遍历:后序遍历是深度优先遍历二叉树的一种方法,它的递归定义是:先后序遍历左子树,再后序遍历右子树,最后访问根。
Output
包括一行,这一行只包含一个字符串,即FBI树的后序遍历序列。
Sample Input 1
3 10001011
Sample Output 1
IBFBBBFIBFIIIFF
没错是线段树,很简单的线段树
本来想用之前的线段树的模板改成答案,发现连lazy数组都不要,简直太友好了,那就直接重大一遍
关键就是对树的维护就不是加减乘除了,而是用字符判断了
#include<stdio.h>
#include<string.h>
char tree[5050];//开这末大是怕最后遍历的时候会下标越界
char a[1050];void nerw(){
for(int j=1;j<=5050;j++){tree[j]='0';
}}void he(int p){//维护数组if(tree[2*p]=='F'||tree[2*p+1]=='F'){tree[p]='F';}else if(tree[2*p]=='I'&&tree[2*p+1]=='B'){tree[p]='F';}else if(tree[2*p]=='B'&&tree[2*p+1]=='I'){tree[p]='F';}else if(tree[2*p]=='B'&&tree[2*p+1]=='B'){tree[p]='B';}else if(tree[2*p]=='I'&&tree[2*p+1]=='I'){tree[p]='I';}}void builtree(int p,int x,int y){
if(x==y){if(a[x-1]=='0'){tree[p]='B';}else{tree[p]='I';}
}
else{int mid=(x+y)/2;builtree(2*p, x, mid);builtree(2*p+1, mid+1,y);
}
he(p);
}void bianli(int p){if(tree[p]!='0'){bianli(2*p);bianli(2*p+1);printf("%c",tree[p]);}else{return ;}
}int main(){
int n;
nerw();
scanf("%d",&n);
scanf("%s",a);
int l=strlen(a);
builtree(1,1,l);bianli(1);return 0;
}通俗易懂,学过线段树的人一看就会
几天没写线段树,现在又相当于复习了哈哈
今天ok了
撒花谢幕!!!!!!