B题 洛谷P7107
题目背景
暑假期间,学校不提供午餐,Gnar 只好找伙计们一起点外卖。
尴尬的是,外卖很快送到却没人乐意去校门口拿,毕竟户外可是 35\degree\!\text{C}35°C 高温!此时 Gnar 想到了好主意:“我给一人捏了一张纸团,其中一张写有记号,不如我们抓阄决定,谁抽到带记号的谁去拿!”
于是 Gnar 连续拿了六天的外卖。
这可让他不服又委屈:“换个规则!一人准备三张纸团,五张有记号,每人抽三张,记号最多的去拿!”
Gnar 紧张地展开手中的纸团,两个记号赫然映在眼前。大伙们刚想放声大笑他的非酋运气,有人缓缓举起三张纸片说道:“我也抽到了两个记号……”
题目描述
好奇的 Gnar 想研究一般情况下抽到最多记号的人数。他给参与抓阄的 nn 人一人准备了 mm 张捏好的纸团,一共 nmnm 张,其中恰好 kk 张提前写了记号。随后每个人在均匀打乱的纸团中各抽 mm 张。
一个人抽到最多的记号,当且仅当没有人抽到的记号比他还多。请你帮 Gnar 判断是否可能会恰好 \boldsymbol{p}p 个人抽到最多的记号。Gnar 喜欢追根问底,所以如果有可能,你还需构造每个人抽的纸团中分别有多少带记号、有多少不带记号。
形式化地,假设第 ii 个人抽到了 x_ixi 张带记号的纸团和 y_iyi 张不带记号的纸团,你的构造应满足:
- x_i, y_i \ge 0xi,yi≥0,x_i + y_i = mxi+yi=m。
- \displaystyle \sum_{i = 1}^{n} x_i = ki=1∑nxi=k。
- 有且仅有 \boldsymbol{p}p 个互不相同的 jj 使 \displaystyle x_j = \max_{i = 1}^{n} \{x_i\}xj=i=1maxn{xi}。
输入格式
输入四个整数 n, m, k, pn,m,k,p,含义详见题目描述。
输出格式
第一行输出 YES 或 NO(不区分大小写,yEs / No 均可),表示是否会恰好 pp 个人抽到最多的记号。
如果第一行输出 YES,接下来 nn 行每行输出 x_i, y_ixi,yi,表示每个人抽到带与不带记号的纸团个数。
因答案可能不唯一,本题采用 Special Judge,只要构造符合题面中的要求均视为正确。
输入输出样例
输入 #1复制
3 3 5 2输出 #1复制
YES
2 1
2 1
1 2输入 #2复制
3 3 3 2输出 #2复制
NO输入 #3复制
3 3 5 3输出 #3复制
NO说明/提示
【样例解释 #1】
样例给出了一种满足题述条件的构造。
【样例解释 #2】
不论如何,记号的分布从高到低只有三种情况:\{3,0,0\}{3,0,0},\{2,1,0\}{2,1,0},\{1,1,1\}{1,1,1},抽到最多记号的人数分别对应 11,11,33。因此无法构造 p = 2p=2 的方案。
【数据规模与约定】
本题采用捆绑测试。你必须通过 Subtask 中所有的测试点才能获得该 Subtask 的分数。
- Subtask #1 (15 points):n,m \le 8n,m≤8。
- Subtask #2 (15 points):n,m \le 100n,m≤100。
- Subtask #3 (20 points):n,m \le 10^5n,m≤105。
- Subtask #4 (10 points):p = 1p=1。
- Subtask #5 (40 points):无特殊限制。
对于所有的数据,保证 1 \le p \le n \le {10}^51≤p≤n≤105,1 \le m \le {10}^91≤m≤109,0 \le k \le n m0≤k≤nm。
题意:n*m张纸条里,有k张含有标记。打乱顺序每个人抽m张纸条,其中恰好p个人拿到了最多的含标记的纸条。假设幸运儿就是拿标记最多的,这题的意思就是幸运儿不是一个,而是p个。是否有这种情况发生,如果有请列出情况。
题解:
我一开始想法是,枚举p个人该拿多少张标记纸条。每个人最多拿m张纸条,那么就直接从1枚举到m。
如果有一个i,也就是p个人每人拿i张标记纸条,使得剩下n-p个人每个人含有标记纸条都小于i,那么这个i就是答案。
但是,很明显,超时。
然后我就想调二分,既然答案已知是在1到m,二分了一下,还是有些特殊情况没弄出来。
然后就是正解:
既然有k张标记纸条,要先给p个人都拿同样的数量,然后再让剩下的n-p人分标记纸条,那么我们为啥不直接尽量让p个人拿尽量多的标记纸条呢?也就是直接让p个人拿k/p张纸条,这样子就少了之前的枚举,且符合题意。但是要注意,也有可能k/p会大于m,所以我们取p个人每人取min(m,k/p)张纸条。设q=min(m,k/p)。
按照题意,剩下的n-p的人就不能超过q,那么就让剩下的人取q-1,然后取到无为止,那不就满足条件了!
但是还是要思考一下如何出现NO,我们现在p个人取q已经是取得最多的情况了,那么只有剩下的标记纸条每人q-1张还出现多了,那就肯定是不符合题意的,就是NO的了。
也就是k-p*q > (n-p) *(q-1)的时候,就是NO的时候。
那么这样就很明显了,思路就是这样。
代码:
#include <iostream>
#include <stdio.h>
#include <math.h>
#include <algorithm>
#include <string.h>
#include <cstring>
#include <string.h>
#include <cmath>
#include <queue>
#include <stack>
#include <vector>
#include <cstdlib>using namespace std;long long n,m,k,p;void read_in()
{ios::sync_with_stdio(false),cin.tie(0);cin>>n>>m>>k>>p;}void work()
{int q=min(m,k/p);if(k-p*q>(n-p)*(q-1)){cout<<"NO";return ;}cout<<"YES"<<endl;for(int i=1;i<=p;i++){cout<<q<<' '<<m-q<<endl;k=k-q;}for(int i=p+1;i<=n;i++){if(k>=q-1){cout<<q-1<<' '<<m-q+1<<endl;k=k-(q-1);}elseif(k>0){cout<<k<<' '<<m-k<<endl;k=0;} elsecout<<0<<' '<<m<<endl;}}int main()
{read_in();work();return 0;
}
C题 洛谷P7106
题目背景
我喜欢安静,你热爱喧闹;我忠于温暖,你酷爱凉爽。
如果任何事物都有反面,那拼接这个世界的颜色呢?
只有白与黑吗?
题目描述
为了形式化地描述颜色,我们引入 RGB 颜色值,用三元组 (r,g,b)(r,g,b) 表示一种颜色,其中 r,g,br,g,b 分别为该颜色的 R 值、G 值、B 值,满足 0 \le r,g,b \le 2550≤r,g,b≤255 且皆为十进制整数。
显然,这套颜色系统一共可以表示 256 \times 256 \times 256 = 16\,777\,216256×256×256=16777216 种不同的颜色。对于颜色 (r,g,b)(r,g,b),定义其反色的 RGB 颜色值为 (255-r,255-g,255-b)(255−r,255−g,255−b)。
然而人们发现,单纯地使用 RGB 颜色值很不方便,复制颜色时要复制三个值。
于是诞生了十六进制颜色码,即形如 #EBA932 长度为 77 的字符串。具体而言:
- 字符串的第一位是
#,为颜色码标识符。 - 字符串的第二、三位是十六进制数码,拼成的十六进制数等于十进制下所示颜色的 R 值。
- 字符串的第四、五位是十六进制数码,拼成的十六进制数等于十进制下所示颜色的 G 值。
- 字符串的第六、七位是十六进制数码,拼成的十六进制数等于十进制下所示颜色的 B 值。
十六进制数码从小到大包含 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F,注意 A,B,C,D,E,F 均为大写。
现在你收到了一组十六进制颜色码,请你输出其反色的十六进制颜色码。
提示:颜色的 RGB 值与十六进制码之间可以相互转换(参考样例解释 #2)
输入格式
一行,输入长度为 77 的字符串,表示原色的十六进制颜色码。
输出格式
一行,输出长度为 77 的字符串,表示反色的十六进制颜色码。
输入输出样例
输入 #1复制
#FFFFFF
输出 #1复制
#000000
输入 #2复制
#EBA932
输出 #2复制
#1456CD
说明/提示
【样例解释 #1】
转换后原色的 RGB 值为 (255,255,255)(255,255,255),反色的 RGB 值为 (0,0,0)(0,0,0),对应十六进制码 #000000。
【样例解释 #2】
转换后原色的 RGB 值为 (235,169,50)(235,169,50),反色的 RGB 值为 (20,86,205)(20,86,205),对应十六进制码 #1456CD。
为避免理解偏差,此处特别解释 #EBA932 转换后 B 值为 5050 的原因:提取字符串的第六、七位,拼成的十六进制数为 (32)_{16}(32)16,则有 (32)_{16} = 3 \times 16^1 + 2 \times 16^0 = 50(32)16=3×161+2×160=50。
【数据规模与约定】
本题共有 10 个测试点,每通过一个测试点可获得 10 points。
对于 10\%10% 的数据,为样例 #1。
对于另外 30\%30% 的数据,输入与输出字符串均不包含大写字母。
对于所有的数据,保证给定字符串为合法十六进制颜色码。
题意:
两个字符组成一个十六进制数,一共3个十六进制数,将其转化为十进制后,设其十进制为x,则将其转化成255-x,然后再重新组成十六进制。
题解:
没什么好说,直接模拟。
#include <iostream>
#include <stdio.h>
#include <math.h>
#include <algorithm>
#include <string.h>
#include <cstring>
#include <string.h>
#include <cmath>
#include <queue>
#include <stack>
#include <vector>
#include <cstdlib>using namespace std;string st;
int len=7;
char c[16]={'0','1','2','3','4','5','6','7','8','9','A','B','C','D','E','F'};void read_in()
{cin>>st;
}void out_ans(int k)
{cout<<c[k/16]<<c[k%16];
}void work()
{int r,g,b,sum=0,ki=1;for(int i=6;i>0;i--){int k;if(st[i]<='Z' && st[i]>='A')k=st[i]-'A'+10;elsek=st[i]-'0';sum=sum+k*ki;ki*=16;if(i==1)r=sum;if(i==3)g=sum;if(i==5)b=sum;if(i%2==1)sum=0,ki=1;}r=255-r;g=255-g;b=255-b;cout<<"#";out_ans(r);out_ans(g);out_ans(b);}int main()
{read_in();work();return 0;
}
D题 P7108
题目背景
遥远的圣地生长着一棵不为人知的灵树,或有万山之高。
但有一日,藏匿于根系的腐朽力量爆发,灵树已无法支撑往日屹立冲天的高度。
题目描述
灵树最初的形态可以看作一棵高度为 {10}^{{10}^{{10}^{10}}}10101010 的满 aa 叉树,高度定义为根结点到叶子结点之间的边数。
受腐朽力量影响,灵树只能维持高度恰好为 hh 的满 bb 叉树形态。为了转换至该形态,灵树有两种魔法:
- 移花:选择一条边 u \to vu→v(uu 是 vv 的父结点),移除这条边以及以 vv 为根的整棵子树。
- 接木:选择一条边 u \to vu→v(uu 是 vv 的父结点)和一个结点 ww(ww 不能是 vv 子树中或已移除的结点),将这条边原先 uu 一端改接到 ww。该魔法只能在根结点到 \boldsymbol{u}u 之间的边数 \le 10^{10^{10}}≤101010 时使用。
灵树累积的魔法力量有限,它不得不用最少次数的魔法完成转换。这是个漫长的过程,即使次数最少也会显得异常大,你只需要求出最少次数对 10^9 + 7109+7 取模的结果。
输入格式
输入首行给定数据组数 TT。
接下来 TT 行,每行包含三个整数 a,b,ha,b,h,表示一组数据。
输出格式
对于每组数据输出一行一个整数,表示该数据的答案对 10^9 + 7109+7 取模的结果。
输入输出样例
输入 #1复制
2 1 2 1 3 2 1
输出 #1复制
2 7
说明/提示
【样例解释 #1】
下为 a=1a=1,b=2b=2,h=1h=1 时的两步转换过程,图中高度极大的冗余子树已用省略号代替。
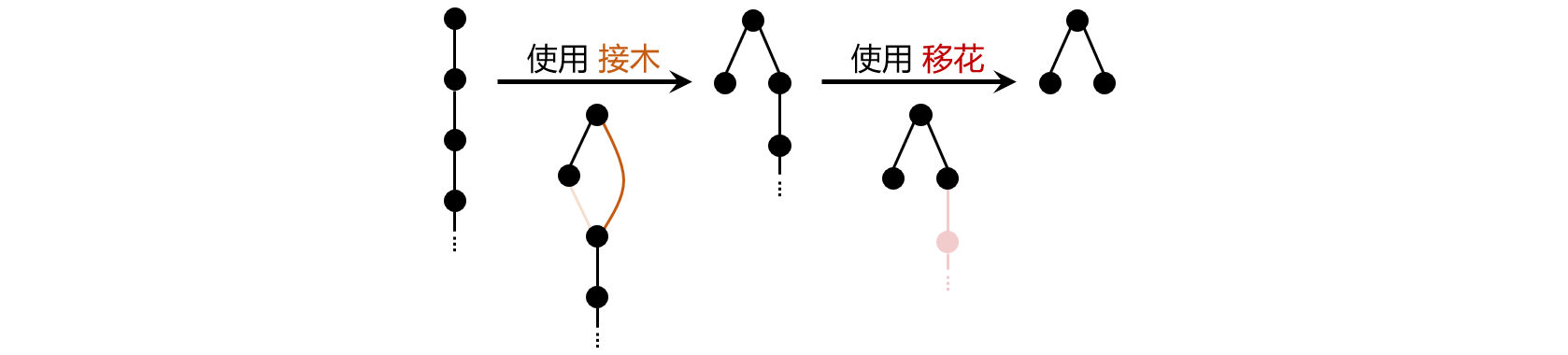
可以证明,该数据的答案不可能低于 22。
【数据规模与约定】
本题采用捆绑测试。你必须通过 Subtask 中所有的测试点才能获得该 Subtask 的分数。
- Subtask #1 (3 points):h = 0h=0。
- Subtask #2 (4 points):a = ba=b。
- Subtask #3 (8 points):a = 1a=1。
- Subtask #4 (8 points):b = 1b=1。
- Subtask #5 (17 points):h \le 10h≤10。
- Subtask #6 (15 points):h \le 10^6h≤106,各测试点存在 \overline{a},\overline{b}a,b,其数据满足 a=\overline{a}a=a,b=\overline{b}b=b。
- Subtask #7 (15 points):h \le 10^6h≤106。
- Subtask #8 (30 points):无特殊限制。
所有测试点(样例除外)均含有 10^6106 组数据,即 T = 10^6T=106。请务必采用较快的 IO(输入/输出)方式。
对于所有的数据,保证 1 \le a,b \le 10^91≤a,b≤109,0 \le h \le 10^90≤h≤109。
题意:
理解为无限高度的满a叉树通过割边舍弃这条边,或者把这条边接到点上,运用这两个操作变成高度为h的满b叉树。
题解:
分类讨论,推公式。
当b>a 的时候的公式很好推,只需要不断的拆h+1层的分支去补,然后再把剩下的h+1层全割掉。很容易推出来公式为 a*(b^h)
当a>=b时,公式有点难推,当时我推出来的是(a-b)(b^h-1)/(b-1)+a*(b^h),但是不知道为什么错了。
但是,即使我们改不对这道题,我们也还是要在其中学到知识。
这题正解需要 “逆元” 来维护,以前就常听逆元是什么了,现在稍微学习一下。
什么是逆元?
如果 b * i 1 (mod p)成立,那么i就是b在mod p 的条件下的逆元。
逆元有什么作用呢?当计算a / b (mod p) 的值时,如果b很大,则经度可能会爆,则我们可以转换为 a * i (mod p),这样子就能避免经度的损失。
如何求逆元?
现在先学了一种快速幂求逆元的方法先。
这个方法运用了费马小定理:若gcd(a,p)==1 ,则 存在 (mod p )。
那么有 (mod p)那么
就是a的逆元。
实话讲现在越打信心越低,慢慢来吧。


