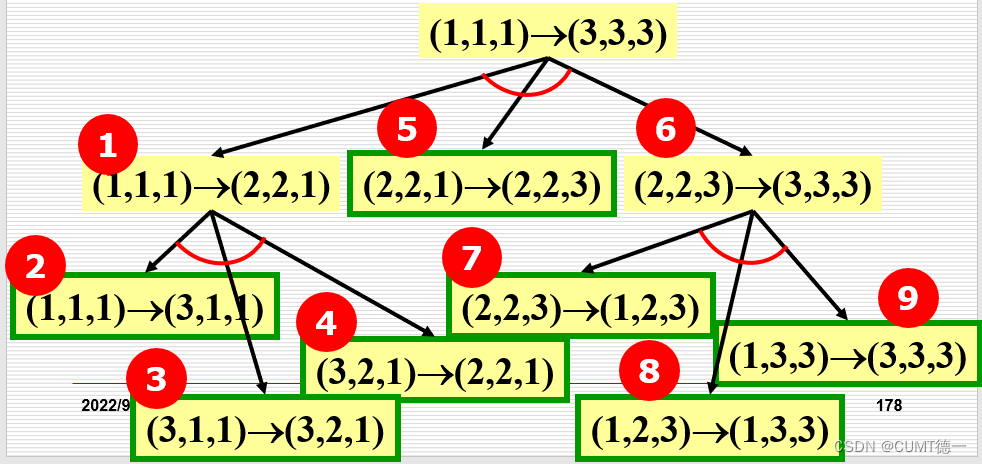
第一下拿到这道题，我的脑袋轰一下就大了。如果说用”括号匹配“来做的话，这其实很简单。但是如果要用广义表来做的话，难度哗哗哗的就涨上来了。为什么呢？首先，要把读入的字符串存到广义表里面去，这里就需要第一次用到递归；然后，对已经构造好了的广义表，还需要进行求深度的递归，这就用到了第二次递归。上面这两次递归就已经足够让人头疼的了，更不用说处理输入中的逗号了。

当然，在这片文章的最后会有完整的代码实现，但是我还是更想去和大家分享一下，在这道题中，应该怎么去构建递归函数，当然这是我今天下午摸索出的一套构建的方法，也有了一些自己的思考，总结了一些好用的技巧。下面跟大家分享一下：

老师曾经教过说读代码可以使用”走读“的方式，也就是说不用电脑，而是只在纸上写写画画。同样的道理，我们在写程序中的算法时，也可以采用这种方法。以两个递归函数中的”字符串存到广义表“为例，我们可以先拿出来一个综合性很强的例子，比如说“(a,(b,c)),(c,(d,e)))"，然后沉下心来一步一步地画它的广义表，在画的时候，你就会情不自禁的想把你发现的东西给写下来，没错，你的感觉是对的！把你发现的东西写到纸上（比如，你会发现”如果表头是a、b、c之类的字母，那么表头上要新创一个tag为0并且变量值为a、b、c这些字母的结点“）。等到你画完了一个完整的广义表，你也会在纸上写下了很多东西。没错，下一步就是编制程序。把你在纸上写下来的东西转换成为具体的代码（这时我发现最有效的方法），你就会发现写程序明显没有之前那么痛苦了。为什么这很有效呢？因为你要知道，电脑是根据人脑制造出来的，所以当你走到程序进程中的某一个地方时，你对于下一步的下意识想法或者行动，很有可能就是你程序中的那个困扰你的那个步骤。

此外，很多情况下，我们写一个成熟的程序经常需要很长时间，经常是一不小心一个上午就过去了，而且临近中午的时候，脑子几乎就是不动的，效率会慢慢变得越来越低。为了应对这种困境，我发现了一种特别好用的方法，就是把一个问题拆分成为几个小问题，然后分时间段完成这几个小问题，最后就能解决这个大问题。以之前的实验”高精度pi值得求解“为例，我是怎么拆分的呢？看下面：

1.搭建用来存放高精度小数的双链表；

2.完成双链表表示的小数与一个整数的乘法（没有发生进位的那种）；

3.完成双链表表示的小数与一个整数的乘法（有发生进位的那种）；

4.完成双链表表示的小数与一个整数的除法；

5.构建主函数。

通过这5步，我总共用了4个小时的时间，从无到有得做完了这个实验。有人会说，可其他不这样做的人，他们也是用的这种方法，思路和你一样，而且用的时间也没有比你慢多少，你能有多少优势？对，没错，优势确实很小，但这是一个很有效的思维工具。当面对简单问题的时候，这种分解复杂问题的思维会拖累你的思维，让问题复杂化，做的还不如其它人快，在考试时如果你用这种方法，那你十有八九会做不完卷子，最后拿一个不及格，因为考试题都是极简单不需要过多思考的题，这是它的局限性。但是当问题很复杂，或者问题综合性特别强，抑或者说这是一个你从来没有见过的工程问题时，这种思维工具就会变得特别有用。当别人束手无策不知从何下手时，你已经明确了自己需要完成几个小任务，每个小任务又需要完成什么，而且因为这些小任务往往比较简单，不需要很多的思考，往往都是可以完成的，这也给了你完成任务之后的成就感。这样子成就感给了你积极的反馈，你就会有更大的信心去完成下一个小任务。这样子相比其他人，你就有了更大更多的优势，最后你就是第一。

话题回到这道题的递归上，就我个人来说，咱们初学者没必要也不应该追求简洁的递归实现，也不应该执着于”直接调用“上，相反，”间接调用“是学习递归的一个很好的桥梁，它能够很好地帮你完成程序的编制，最后很快很好的写出行之有效的程序来。

最后，大一作为一个过渡阶段，纸和笔还是有着它无可替代的作用，不要眼高手低，低下头来踏踏实实做事情，在纸上写写画画，往往能提供给你写程序的关键思路。

最后还是真心求赞啦，你们的鼓励是对我创作的最大支持！

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<math.h>
typedef enum{ATOM,LIST}ElemTag;
//ATOM==0,原子,LIST==1,子表
typedef char AtomType;
typedef struct _GLNode{ElemTag tag;union{AtomType atom;struct{struct _GLNode* head;struct _GLNode* tail;}ptr;};
}*GList;GList InitGList(){//创建空的广义表LGList L=(GList)malloc(sizeof(struct _GLNode));if(L==NULL){printf("Out of space!\n");return NULL;}else{L->ptr.head=NULL;L->ptr.tail=NULL;return L;}
}void StringDividing(GList L,char* ori_str,char* s_head,char* s_tail);
void Head_Recursion(GList L,char* s_head){if(*s_head=='('){char sub_s_head[50]={0};char sub_s_tail[50]={0};StringDividing(L,s_head,sub_s_head,sub_s_tail);}
}void Tail_Recursion(GList L,char* s_tail){if(*s_tail!='0'){char sub_s_head[50]={0};char sub_s_tail[50]={0};StringDividing(L,s_tail,sub_s_head,sub_s_tail);}
}void StringDividing(GList L,char* ori_str,char* s_head,char* s_tail){char* temp=ori_str+1;//将字符串分成“表头字符串”和“表尾字符串”//然后用"s_head"存放表头字符串//再用"s_tail"存放表尾字符串 //下面先处理"s_head": //如果s_head中只有一个字符，那么： if(*temp!='('){*s_head=*temp;//并且创建一个原子结点 GList Atom=InitGList();Atom->tag=ATOM;Atom->atom=*temp;//然后让当前结点的表头指针指向它L->ptr.head=Atom;}//但如果s_head中不止一个字符，就应该： else{//首先，确定"s_head"中要放多少字符： int fre=0;while(1){temp++;if((*temp!='(')&&(*temp!=')'));else if(*temp=='(') {fre++;}else if(*temp==')') {if(0!=fre) fre--;else break;}}//确定好了之后，就可以往"s_head"中放字符了： char* record=ori_str+1;//记录s_head的初始位置，如果不这样做，那么递归传过去的数组指针就有问题for(char *p=ori_str+1;p<=temp;){*s_head=*p;p++;s_head++;}//最后不要忘记末尾置0 *s_head='0';//并且新建一个子表结点GList list=InitGList();list->tag=LIST;//然后让当前结点的表头指针指向它 L->ptr.head=list;//再然后，还需要把当前的"s_head"送去递归分割 Head_Recursion(list,record);//record记录的是s_head的初始位置 }//然后再处理"s_tail"://分两种情况来讨论：//1.如果表尾是空表的话，那么：if(*(temp+1)==')'){//当前结点的表尾指针置为NULL即可L->ptr.tail=NULL; }//2.如果表尾不是空表的话，那么： else{//因为表尾一定是表，所以还需要用"()"，把它再给包起来 //先在数组头儿上放"("：char* record=s_tail; //记录s_tail的初始位置，如果不这样做，那么递归传过去的数组指针就有问题 *s_tail='(';s_tail++;//然后放中间，因为很容易确定"s_tail"中要放多少字符，所以直接往里面放就可以：for(char *p=temp+1;*p!='\0';){*s_tail=*p;p++;s_tail++;}//最后需要在数组尾儿上放")"，但是因为ori_str最后自带一个")"，所以不用多费心 *s_tail='0';//并且新建一个子表结点GList list=InitGList();list->tag=LIST;//然后让当前结点的表尾指针指向它L->ptr.tail=list; //再然后，还需要把当前的"s_tail"送去递归分割 Head_Recursion(list,record);//record记录的是s_tail的初始位置 }
}int GListDepth(GList L){//递归获取广义表深度if(L==NULL) return 1;//空表深度为1else if(L->tag==ATOM) return 0;int max=0;GList pp=L;for(;pp!=NULL;pp=pp->ptr.tail){int dep;dep=GListDepth(pp->ptr.head);if(dep>max) max=dep;}return (max+1);
}int main(){//创建最初的广义表 GList L=InitGList();L->tag=LIST;//从键盘中录入原始字符串 char ori[250]={0};scanf("%s",ori);//对原始字符串进行处理，去除里面的逗号char ori_str[250]={0};char* p1=ori;char* p2=ori_str;while(*p1!='\0'){if(*p1==','){p1++;}else{*p2=*p1;p1++;p2++;}}char s_head[50]={0};char s_tail[50]={0};StringDividing(L,ori_str,s_head,s_tail);int depth=0;depth=GListDepth(L);//获取广义表深度 printf("%d\n",depth);printf("%d\n",depth);return 0;
}