算术逻辑单元ALU

请添加图片描述
运算器的内部除了包含一些必要的寄存器之外，用于实现运算的核心部件就是算术逻辑单元(ALU)。
ALU主要有以下功能：

算术运算：加、减、乘、除等
逻辑运算：与、或、非、异或等
辅助功能：移位、求补等

ALU的大致结构如下：
请添加图片描述
$A_i$ 和 $B_i$ 为输入信号，比如说要实现两个8比特二进制数的加法，那么其中一个从 $A_i$ 端输入，另一个从 $B_i$ 端输入，输入的本质是一些电信号（高低电平），输出信号（运算结果）从 $F_i$ 端输出， $K_i$ 为控制信号，由控制单元CU发出。

例子：74181芯片
在这里插入图片描述
右边的 $S_3 S_2 S_1 M$ 是来自控制单元的控制信号，控制单元会负责解析指令的含义，然后根据这个指令的含义发出一些控制信号，如： $M=1,S_3 S_2 S_1 S_0=1001$ 时，做逻辑运算 $\oplus B$ , $S_3 S_2 S_1 S_0$ 有4比特信息，即对应 $2^4=16$ 中状态，说明此芯片支持16种算数运算或16种逻辑运算。 $A_i、B_i和F_i$ 与上一张图对应上分别为输入信号和输出信号。

机器字长，指计算机能够同时处理多少个比特位的整数运算，即ALU里面可以支持同时输入多少个比特的信息。一般来说，ALU可以处理多少比特的数据，通常就会把寄存器 $X$ 的位数和ALU的位数保持一致。上图种，ALU输入了两个4bit的信息，然后输出一个4bit的运算结果，这个结果要放回到某一个寄存器里面，为了能让ALU与寄存器能够完美地适配，ALU是多少位，寄存器也对应设计为多少位。

左边的输出信号和下边的 $C_{-1}$ 输入信号是为了和其他芯片进行串联而设计的。

最基本的逻辑运算

请添加图片描述
A和B是输入信号，Y是输出信号。比如说，对于与门，A输入5V的电信号为1，B输入1V的电信号为0，则Y会输出1V的电信号为0，即1和0相与得到0.
注：非门的电路图种右边有一个小圆圈。

类比乘法、加法

与运算和或运算的优先级：与>或（Eg：AB+CD先算与，再算或）
A(C+D)=AC+AD ——分配律
ABC=A(BC) ——结合律
A+B+C=A+(B+C) ——结合律

这有何意义？
本质上，逻辑表达式是对电路的数学化描述，简化逻辑表达式，就是在简化电路，而这些器件是需要钱的，那么简化电路就是在省钱。
例子：
电路实现AC+AD=A(C+D)
可以看到，右边的实现方式比左边的实现方式少了一个与门。
请添加图片描述

复合逻辑运算

请添加图片描述
反演率（德摩根率）： $\overline{A+B}=\overline{A}\cdot \overline{B},\overline{A\cdot B}=\overline{A}+\overline{B}$

任何使用与、或、非实现异或运算？
->A和B不同则为1
->A=0且B=1 或者 A=1且B=0
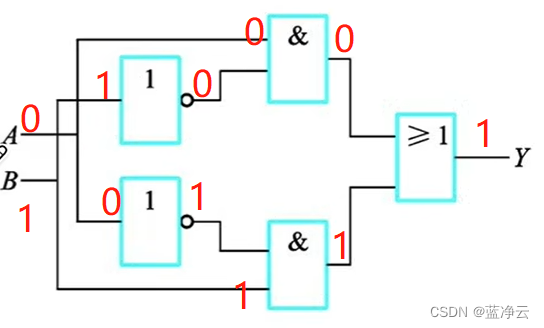
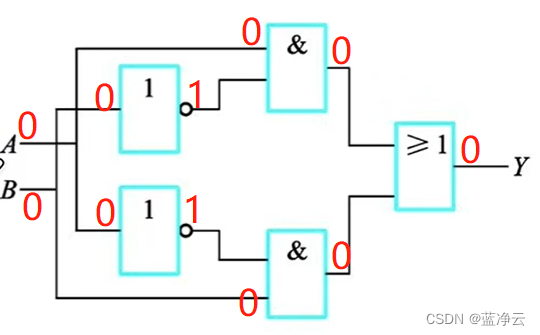
-> $\overline{A}\cdot {B}+{A}\cdot \overline{B}$
电路实现：
请添加图片描述

用门电路求偶校验位

“异或”的天然逻辑：“加法”“奇偶校验”
偶校验就是当我们加入了这个校验位之后，整体来看，1的数量总共有偶数个。
在这里插入图片描述

偶校验的逻辑和异或的逻辑对应，对偶数个1进行异或，最终得到的结果是0，对应于偶校验需要得到的校验位。奇校验的逻辑和异或的逻辑对应，对奇数个1进行异或，最终得到的结果是0，对应于奇校验需要得到的校验位。
在这里插入图片描述
下面位求偶校验位的电路图：
请添加图片描述

一位全加器

异或门如何实现加法运算？
首先从手算加法出发。
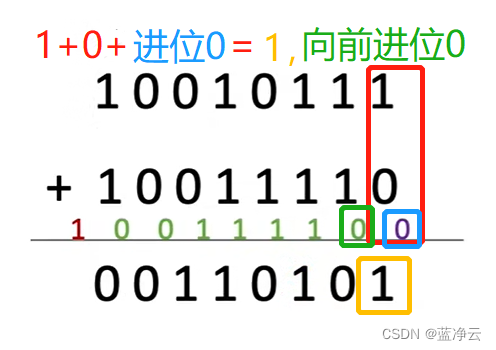
请添加图片描述
$S_i和C_i$ 如何确定？
输入中有奇数个1时， $S_i$ 为1（异或） $S_i=A_i \oplus B_i \oplus C_{i-1}$ ;有两种情况 $C_i$ 为1，第一种是两个本位为1，即 $A_iB_i$ 都为1，即 $A_iB_i=1$ ，另一种情况是两个本位中有一个1，且来自低位的进位 $C_{i-1}$ 是1，即 $(A_i \oplus B_i )C_{i-1}=1$ 。
在这里插入图片描述
根据这两个逻辑表达式就可以得到与之相对应的电路，如下图

这就是一位全加器，根据两个本位和低位的进位作为输入，可以确定本位和 $S_i$ 和向高位的进位 $C_i$ ，将上图简化，屏蔽它内部的电路细节，如下图
请添加图片描述

串行加法器

接下来看一下如何用一位全加器来实现多位加法。
顾名思义，所谓串行就是一位一位地加，增加一个进位触发器，用来保存进位位，以此来实现一位一位地加。
请添加图片描述
$A_iB_iC_{i-1}$ 经过一位全加器可以确定 $S_i$ 和 $C_i$ ， $C_i$ 保存到进位触发器中，接下来就可以输入更高位的信息 $A_{i+1}B_{i+1}C_i$ , $C_i$ 的值来自于进位触发器作为输入信号，以此类推。

串行加法器：只有一个全加器，数据逐位串行送入加法器进行运算。进位触发器用来寄存进位信号，以便参与下次运算。
如果操作数长n位，加法就要分n次进行，每次产生一位和，并且并且串行逐位送回寄存器，所以这种串行加法器的效率是比较低的。

并行加法器

请添加图片描述
串行进位的并行加法器：把n个全加器串接起来，就可以进行两个n位数的相加。

这样就可以同时输入两个n位的数，A和B这两个操作数都有n位，每一组对应的位都会用全加器进行相加，并且低位的加和产生的进位会作为下一个全加器的输入信号，虽然刚开始我们就可以同时输入A和B这两个数的各个数值位信息，电器的实际运行速度很快，然而，这些电信号的传递依然是需要时间的，也就是说，只有更低位的运算执行结束之后，才可以确定应该往高位进一个什么样的信号，如果往高位进的信号发生了改变，高位的和还有往更高位的进位信号也会发生改变。所以，这种并行加法器称为串行进位的并行加法器，进位信息都是串行着一位一位往前进的。

串行进位行波进位，每一位进位直接依赖于前一级的进位，即进位信号是逐位形成的，所以这种加法器的运算速度很大程度上依赖于每一位进位的产生速度和传输速度。那这个问题如何优化呢？

ALU的改进

如何更快地产生进位呢？让我们将进位 $C_i$ 的表达式展开：
请添加图片描述
如果把 $C_i$ 一直展开，总有一天可以展开到 $C_0$ ，而 $C_0$ 是最开始就拥有的信息。

结论：第i位向更高位的进位 $C_i$ 可根据被加数和加数的第1~i位，再结合 $C_0$ 即可确定。

记 $G_i=A_iB_i,P_i=A_i\oplus B_i$ ，得到以下表达式：
请添加图片描述

从以上展开式可以看出，即使我们要计算的是 $C_4$ 这个进位信息，刚开始就把所有的计算所需要的数据都准备好了，那么只需要根据表达式设计相应的电路就可以在第4个全加器那里直接算出全加器的值。这样的设计方案几乎每一位的进位信息都是同时产生的，无需再像之前的设计那样要等待后面的进位一位一位地往上传，所以这种加法器的计算速度会快很多。我们把它称为并行进位的并行加法器：各级进位信号同时产生，有称为先行进位、同时进位。
请添加图片描述
这种设计的缺陷：从 $C_1到C_4$ 我们一度往下套娃，套得越深，逻辑表达式就越长，电路就越复杂。

比较经典你的做法是，套到 $C_4$ 的位置，即可以支持4位加4位的运算。
请添加图片描述
如果我们需要更多的比特位进行加法，只需要将4位CLA加法器进行串联即可。

并行加法器的优化

单级先行进位方式，又称为组内并行、组间串行进位方式。
请添加图片描述
组内进位可同时得出，但组间的进位又会产生之前的问题，即要先确定第一组的 $C_4$ ，第二组的 $C_8S_8S_7S_6S_5$ 才可以确定，要一步一步往前传，那么如何优化此问题呢？
继续套娃！！！

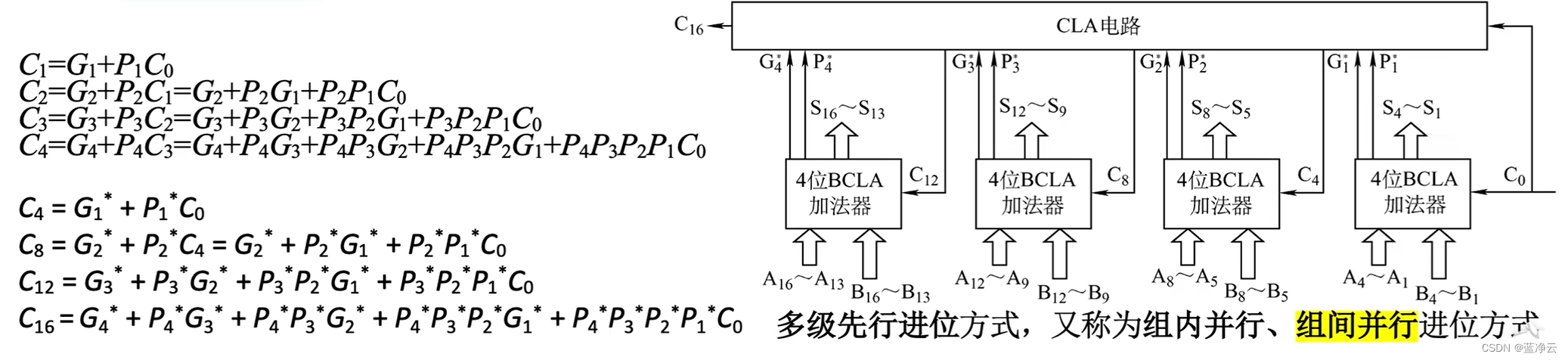
记 $G_{1}^{*}=G_4+P_4G_3+P_4P_3G_2+P_4P_3P_2G_1；$
$P_{1}^{*}=P_4P_3P_2P_1$
请添加图片描述

核心特性：根据本组的4×2个输入位即可确定本组的 $G_{i}^{*}P_{i}^{*}$ 。

组间进位信息的运算规则与组内进位信息的运算规则完全可以对应上，也就是说，把 $G_{1}^{*}、P_{1}^{*}、G_{2}^{*}、P_{2}^{*}、G_{3}^{*}、P_{3}^{*}、G_{4}^{*}、P_{4}^{*}$ 作为CLA的输入，那么CLA内部的电路就可以帮我们完成对 $C_4、C_8、C_{12}、C_{16}$ 的运算。

ALU芯片的优化

把上面的电路进行改造，将每4个比特进行一个分组，进行4bit+4bit的运算，将CLA的内部线路进行改造（BCLA），让它输出这个分组的 $G_{i}^{*}和P_{i}^{*}$ ，然后 $G_{i}^{*}和P_{i}^{*}$ 作为CLA电路的输入，而CLA内部则可以并行得出 $C_4、C_8、C_{12}、C_{16}$ 的值，即每一个分组在计算本位和的时候需要作为参考的进位信息不需要像之前那样等着从后面一个一个往前传，所以采用这种思想来实现电路，可以实现组内并行、组间并行的进位方式，每一组所需的进位信息都是并行产生的，因此电路的运算效率再一次提升。
请添加图片描述
74181芯片支持实现4位的加法运算，下图中 $C_{n+4}$ 为两个4位的比特信息相加之后向更高位的进位， $C_{-1}$ 是来自低位的进位。

所以利用线路把4个74181串行起来就可以实现16位的组内并行、组间串行的进位ALU。
请添加图片描述
如果再接上一个SN74182芯片，那么我们就可以实现16位的组内并行、组间并行的进位ALU。

总结：串行加法器→串行进位的并行加法器→组内并行、组间串行进位的加法器→组内并行、组间并行进位的加法器