前言

上一节内容我们学习了链表的有关内容，今天我们将进行栈的学习；栈也是一种十分重要的数据结构；就让我们一起进入到今天的学习当中吧！！！！！！

提示：以下是本篇文章正文内容，下面案例可供参考

一、栈的基本认识

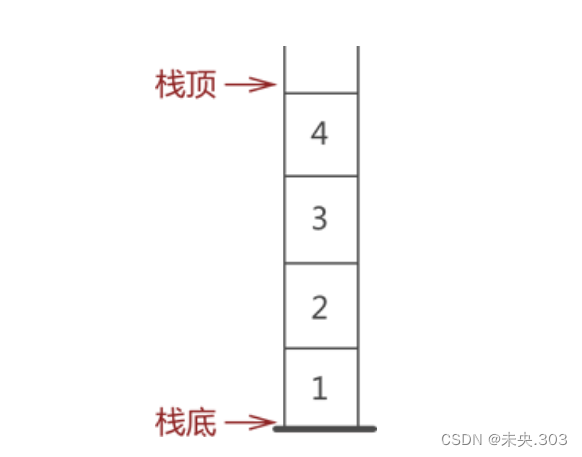
同链表和顺序表一样，栈也是用来存储逻辑关系为 "一对一" 数据线性数据结构，如图所示。

从图中我们看到，栈存储结构与之前所学的链表和顺序表有所差异，这缘于栈对数据 "存" 和 "取" 的过程有特殊的要求：

1.栈只能从表的一端存取数据，另一端是封闭的；
2.在栈中，无论是存数据还是取数据，都必须遵循"先进后出"的原则，即最先进栈的元素最后出栈。拿图中的栈来说，从图中数据的存储状态可判断出，元素 1 是最先进的栈。因此，当需要从栈中取出元素 1 时，根据"先进后出"的原则，需提前将元素 3 和元素 2 从栈中取出，然后才能成功取出元素 1。

因此，我们可以给栈下一个定义，即栈是一种只能从表的一端存取数据且遵循 "先进后出" 原则的线性存储结构。

通常，栈的开口端被称为栈顶；相应地，封口端被称为栈底。因此，栈顶元素指的就是距离栈顶最近的元素，同理，栈底元素指的是位于栈最底部的元素；

那么了解了栈的基本结构，在栈中我们如何实现元素的增加和删除呢？

从上面的图我们不难发现，在栈中我们无论是放元素还是取元素，顺序都是从上到下，即都是从栈顶开始、到栈底结束，所以增加和删除的也是通过栈顶来实现的，即我们删除一个元素就是把当前栈顶的元素给挪开，让该元素下面的元素变成新的栈顶；我们增加一个元素就是让新增加的元素变成我们新的栈顶；

我们存放数据的过程就叫做入栈
我们取出数据的过程就叫做出栈

二、栈模拟实现：

别看说了这么多其实栈的实现很简单，不信你看

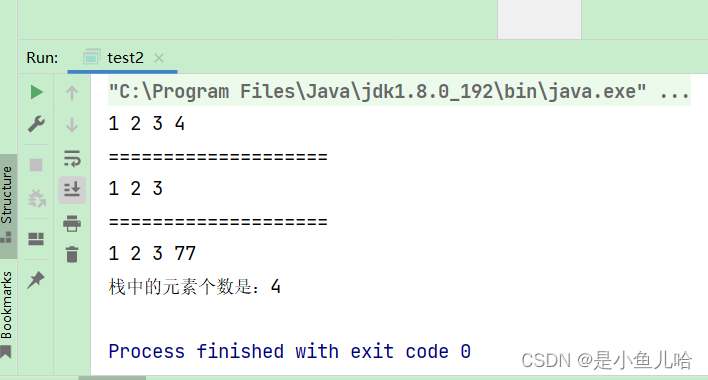
public class MyStack {public int[] elem;public int usedSize;MyStack() { // 栈的初始化elem = new int[]{1, 2, 3, 4};usedSize = elem.length;}public void push(int val) { // 默认相当于是尾插, 来入栈elem[usedSize] = val;++usedSize;}public void pop() { // 出栈if (empty()) {System.out.println("当前栈为空，你的操作不合法！");return;}--usedSize;}// 判断栈是否为空, 空则返回true，非空则返回falsepublic boolean empty() {if (usedSize == 0) return true;return false;}// 获取栈中元素的个数public int size() {return usedSize;}// 顺序打印当前栈中的所有元素public void printMyStack(){for (int i = 0; i < usedSize; i++) {System.out.print(elem[i] + " ");}System.out.println();}
}

运行结果如图所示：

三、栈的实战演练

3.1 有效的括号

题目链接 ：

有效的括号——力扣

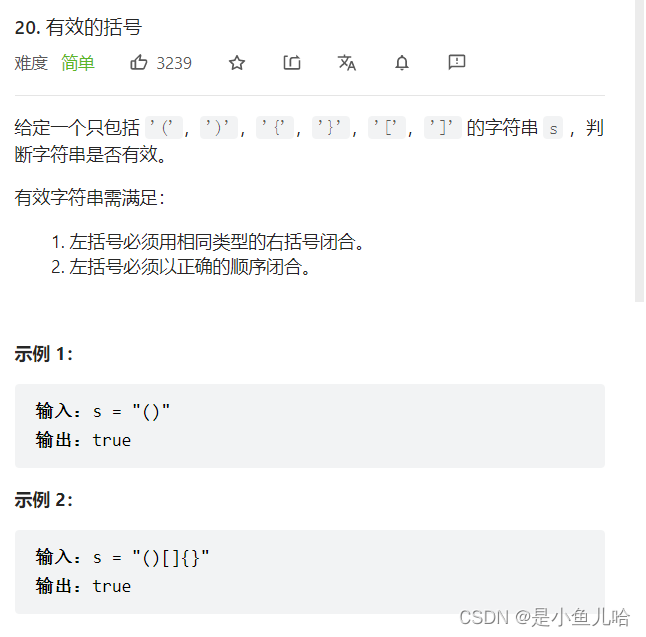
本题的思路：

只要所给字符串的左右两边是对称的——就合法；

即字符串中左右括号的个数是相当的，注意这里所说的左右括号各有三种类型——"{}、[]、()"

我们不妨用栈来储存左括号，借助栈来看看左右括号的个数是否相等；

再对该字符串进行遍历的过程，如果我们的右边的元素和储存在栈中的左括号相对于，则把当前栈中的所匹配的元素出栈，继续对字符串遍历；

🍑当字符串遍历完后，如果栈中的元素刚好为空，则说明该字符串有效；

🍑如果字符串遍历完后，栈中依然有元素，说明左括号多；

🍑如果字符串还没遍历完，栈就为空了，说明右括号多；

代码分析：
class Solution {public boolean isValid(String s) {Stack<Character> stack = new Stack<>();for(int i = 0; i < s.length(); ++i) {char ch = s.charAt(i);if (ch == '{' || ch == '[' || ch == '(') {stack.push(ch);  // 如果是左括号则入栈}else { // 如果是右括号则与栈中左括号相比，看是否相匹配if (stack.empty()) return false; // 当然如果右括号所对应的右边元素为空，自然是不匹配// 注意此时我们并没有取出栈中的元素（因为还不确定这对括号是否匹配），只是显示当前的堆栈元素char top = stack.peek();if ( (top == '{' && ch == '}') || (top == '[' && ch == ']') || (top == '(' && ch == ')') ) {stack.pop();}else{return false; // 说明此时右边的元素和栈中所存放的左边的元素不匹配}}}if (!stack.empty()) {return false;}return true;}
}

3.2 逆波兰表达式

原题链接

对于这个题目，首先我们需要先补充一点知识；

中缀表达式转后缀表达式

比如（1 +（2 * 3））+ （（4 * 5） + 6）* 7）这样的中缀表达式要变成像123*+45*6+7*+这样的后缀表达式。

🍑步骤如下：

1、首先将中缀表达式的各个括号对都用不同的颜色清晰的标出来，像这样：

2、然后把运算符符移动到相邻的最近的括号对的后边，（先移动里面的运算符，再移动外面的运算符，然后从前往后的进行移动）

比如对于（1 +（2 * 3））就是先把*号移动——》（1 +（23）*）

然后再是+号——》（1（23）*）+

3、最后再把括号去掉才变成了123*+45*6+7*+这种形式

总结：

1)先按照运算符的优先级对中缀表达式加括号，变成( ( a+(b*c) ) + ( ((d*e)+f) *g ) )

2)将运算符移到括号的后面，变成((a(bc)*)+(((de)*f)+g)*)+

3)去掉括号，得到abc*+de*f+g*+

后缀表达式求值：

那么如何像这种后缀表达式123*+45*6+7*+如何进行求值你呢？这就要借助我们的栈了。

1.建立一个空栈 stack。
2.遍历后缀表达式（此后将遍历到的字符称为 s）。
3.当 s 为数字时，将其压入 stack 栈。
4.当 s 为运算符时，弹出 stack 栈顶和次栈顶的两个数字，并将两个数字按照运算符 s 进行运算，然后将运算结果压入stack 栈。
5.当遍历结束时，存留在栈 stack 中还剩下唯一一个数字，该数字便是运算结果。

下面用例子来解释一下：

举例说明：

假定待求值的后缀表达式为：6 5 2 3 + 8 * + 3 + *，则其求值过程如下：

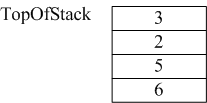
1）遍历表达式，遇到的数字首先放入栈中，此时栈如下所示：

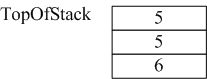
2）然后遇到了 + 这个运算符，那么就把当前的栈顶和次栈顶取出来，进行加法运算，但要注意运算时候次栈顶再前面，栈顶再后面，即次栈顶+栈顶的顺序来进行运算（其他的减乘除也都是按照次栈顶、栈顶这样的前后位置来进行运算的）

3）再把刚才的运算结果5放到栈中，成为新的栈顶；

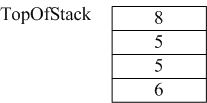
4）然后又继续向后走，把接下来的数字8入栈，成为栈顶；

5）遇到 * 号后，取出栈顶和次栈顶进行 * 的运算——》5，把新的运算结果作为新的栈顶放到栈中；

6）这样当遍历结束时，存留在栈 stack 中还剩下唯一一个数字，该数字便是运算结果；

代码分析：

class Solution {public int evalRPN(String[] tokens) {Stack<Integer> stack = new Stack();for (int i = 0; i < tokens.length; ++i) {String s = tokens[i]; if (charge(s)) { // 如果是运算符，则进行运算操作int num1 = stack.pop();int num2 = stack.pop();switch(s) { // 对从栈顶和次栈顶取出的元素进行运算case "+":stack.push(num2 + num1); // 把运算的结果放回栈中break;case "-":stack.push(num2 - num1);break;case "*":stack.push(num2 * num1);break;case "/":stack.push(num2 / num1);break;        }}else { // 不是运算符，就存在栈中stack.push(Integer.parseInt(s)); // 因为我们的栈中储存的是字符，所以要用Integer中的parseInt进行类型转换}}return(stack.pop()); // 栈中最后一个元素给出栈}public boolean charge(String str) { // 判断当前字符串是否是有效的运算符if (str.equals("+") || str.equals("-") || str.equals("*") || str.equals("/")) {return true;}return false;}
}

3.3 栈的压入、弹出序列

原题链接:

栈的压入和弹出——牛客

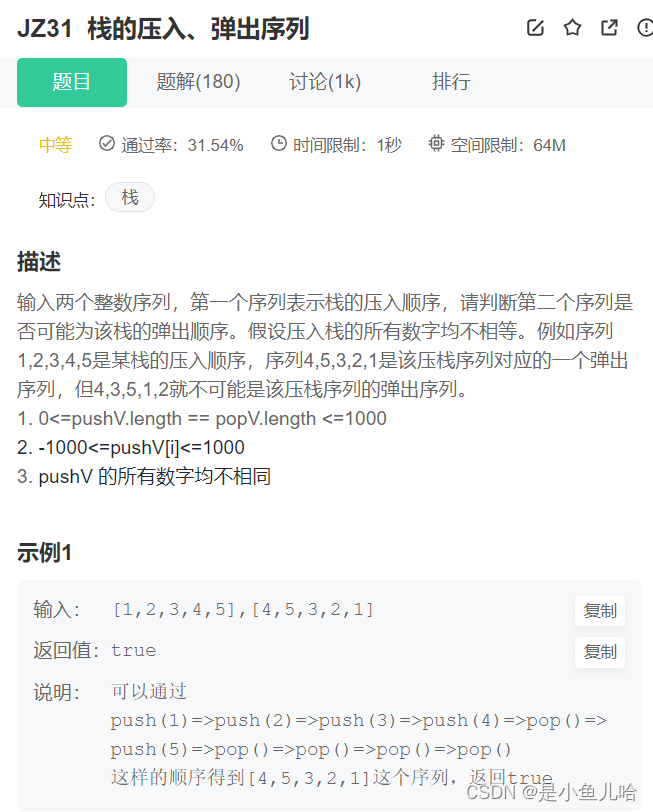
详细的题解和思路可以看看这篇文章:

转载：栈的压入和弹出题解——牛客

代码解析：

import java.util.*;public class Solution {public static boolean IsPopOrder(int [] pushA,int [] popA) {int j = 0;// 用到了一个辅助栈Stack<Integer> stack = new Stack<>();for (int i = 0; i < pushA.length; i++) {stack.push(pushA[i]); // 把while (!stack.empty() && j < popA.length && stack.peek() == popA[j]) {stack.pop();++j;}}if (stack.empty()) {return true;}return false;}}