k-均值（k-means)聚类

k-均值聚类实际上是多元统计分析中的聚类分析部分的内容，但是也是机器学习的基础算法。它的目的就是把数据（无标签）进行分类，但是具体分多少个类却不知道，只能我们先认为的假设分为多少个类进行计算。

聚类与分类是有着本质区别的。对于分类问题及其算法算法（如逻辑回归、支持向量机等分类算法），它们属于监督学习——根据原有的数据（有标签类别）和对应的类别进行训练，训练后可以把新的未知类别的数据进行预测判别其属于哪一类；而聚类则是只有一堆数据，我们不知道类别（即无标签），而是人为地进行分类。简单来说，分类问题，就好比人们经过了以往的学习，我们知道绿豆是绿色的，红豆是红色的，当看到一个红色的圆状物体我们就认为他很可能是红豆；聚类问题，就好比我们收获了很多苹果，然后把大一点的放一堆，中等放一堆，小一点的放一堆，做一下分类，具体分多少堆以及大小指标在于人们的意愿。

所以，当我们了解聚类问题后，就应该去想如何进行聚类。而k-均值聚类就属于聚类算法之一，也是一种比较简单的算法。

（1）算法思想

我们前面讲到了苹果分堆的聚类例子。比如我们就分两堆苹果，那通常肯定是大的放一堆，小的放一堆，所以每一堆里面苹果大小差别不大，比较相似。

而对于数据聚类，也是同样的思想，我们让每一类内的数据距离尽可能的近（即相似）。那么数据间的距离（相似度）如何度量呢？

在多元统计中，数据之间的距离有很多的度量方法，如欧式距离、切比雪夫距离、马式距离、兰式距离等等。关于距离的度量方法兔兔在另外的文章单独讨论。本文为了方便讲述算法，采用欧式距离度量方法，即

$d(X^{(i)},X^{(j)})=\sum_{k=1}^{p}\sqrt{|X^{(i)}_{k}-X^{(j)}_{k}|^{2}}$

其中 $X^{i},X^{j}$ 分别表示第i组、第j组数据。k表示每组数据内第k个指标，总共有p个指标。对应苹果，如果只根据大小分类，指标p=1个；如果根据大小、颜色、味道进行分类，那么指标p=3个。每一组数据就对应一个苹果。

在采用了欧式距离度量方法之后就是该进行聚类了。在开始时，我们需要人为确定聚类成多少个种类。当我们确定分为n个种类后，初始时把所有数据随机分成n类。并计算每一类的中心点。（这里的中心点就是求和平均，例如对于第i组数据（x11,x12),（x21,x22),(x31,x32),那么这个组的中心点就是 $(\frac{x11+x21+x31}{3},\frac{x12+x22+x32}{3})$ 。

之后就是对所有的点（数据）遍历一遍，每一个点计算到n个类中心的距离，然后把这个点归到那个距离最近的那个类。比如数据 $x^{(i)}$ 到第n组的数据中心是最近的，那么就把这个数据放到第n类。所有点变量后，就形成了新的n个类。

之后对这新的n个类再求中心点，再遍历所有的点，重复前面的过程，就又更新一遍。

这样，执行循环多次，最终就可以实现聚类了。这个也就是k-均值聚类的所有过程。

（2）算法流程

（1）初始时把m个数据随机分成n类（一般都是平均分，每个类里面数据个数相同）。

（2）计算每个类里面数据的平均值，得到n个类的中心点。

（3）计算所有数据（每个点）到各个中心的距离，把这个点归到距离最近的那一类。

（4）所有点遍历后得到新的聚类。再计算这n个类的n个中心点。

（5）重复（3）的操作，再（4），一直循环多次。

（6）多次循环结束后，得到聚类结果。

（3）算法实现

我们以下面的数据为例，该数据有两个指标，可以表示为二维平面的点。

x=[1,2,3,4,3,2,6,5,4,3,10,12,24,33,45,44,22,50,44,30,31,29,20,21,24,24,22,23,15,12,11,9,15,14,12,8,6,29,22,44]
y=[5,2,8,1,9,3,9,2,1,5,11,33,20,22,39,42,50,50,40,40,31,40,30,20,31,44,50,48,9,8,10,3,3,4,8,7,8,25,39,20]
data=list(zip(x,y))

散点如下所示：

我们通过直觉可以发现左下角可以分成一堆，右上也可以分为一堆，所以可以设分为两类。

class k_mean:def __init__(self,data,n=2,circle=10):self.circle=circleself.data=data #待聚类的数据self.n=n #把数据分成的类数self.category=[]self.m=len(data) #数据个数self.mean=[] #用来储存每个类的中心点for i in range(n):self.category.append([])def distance(self,x,y):'''计算数据之间的距离,采用欧式距离'''n=len(x) #判断数据的维数s=0for i in range(n):s+=(x[i]-y[i])**2return np.sqrt(s)def main(self):'''聚类过程'''l=int(self.m/self.n) #l为初始的每个类里面元素的个数for i in range(self.n-1):self.category[i]=data[i*l:i*l+l] #把数据分别分到各个类中self.category[-1]=data[l*(self.n-1):self.m] #防止m无法被n整除的情况，把剩下的数据放最后一类数据for i in range(self.circle):'''开始循环'''category=[[] for i in range(self.n)] #用来储存遍历后点的分类print('the {} epoch'.format(i))for j in range(self.n):self.mean.append(np.mean(self.category[j],axis=0)) #求各个类的中心点并保存到mean中for j in range(self.m): #开始遍历各个点：d=[] #用来保存数据点j到各个中心的距离for k in range(self.n):d.append(self.distance(data[j],self.mean[k]))index=d.index(min(d)) #找到离这个点最近的那一类,类为第indexcategory[index].append(data[j]) #把这个点加到那一类中self.category=category #把新聚类传递到self.category中，用于下一次计算中心点，同时下一次category清空return self.categoryif __name__=='__main__':x=[1,2,3,4,3,2,6,5,4,3,10,12,24,33,45,44,22,50,44,30,31,29,20,21,24,24,22,23,15,12,11,9,15,14,12,8,6,29,22,44]y=[5,2,8,1,9,3,9,2,1,5,11,33,20,22,39,42,50,50,40,40,31,40,30,20,31,44,50,48,9,8,10,3,3,4,8,7,8,25,39,20]data=list(zip(x,y))k=k_mean(data=data)c=k.main()print(c)for i in c:x=[]y=[]for j in i:x.append(j[0])y.append(j[1])plt.scatter(x,y)plt.show()

其实如果自己定义分类个数和已知指标个数，算法实现要比上面简单很多，距离就直接两点做差求平方和后开方；而且如果知道分类个数，可以初始类C1、C2...，构造这些空列表，每次往里加数值，之后求平均，而且初始时也不需考虑数据个数是否被类整除的情况。但是兔兔上面写的k-mean则更具有普适性，如果打算把样本分几类，只需改变参数n即可，而且样本的指标的个数也是任意的，可以是二维、三维、四维等，但是处理过程也更复杂一些。所以k-均值算法难点不在流程，而在于算法的完整实现。程序结果如下：

我们发现，运行结果于预想的是一致的。如果我们把它分成三类，则结果如下：

我们发现，效果也是可以的。

其实，对应一些随机的散点，也都是可以用k-均值计算的，虽然我们看起来这些点没有太多规律。但这种情况有时聚类也是没有太大意义的。如下图所示。

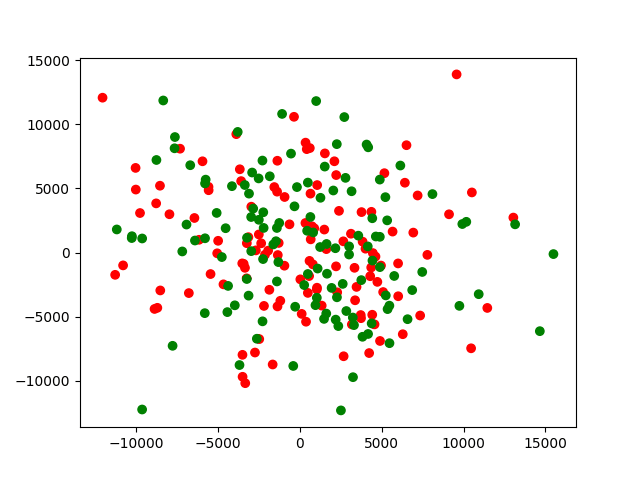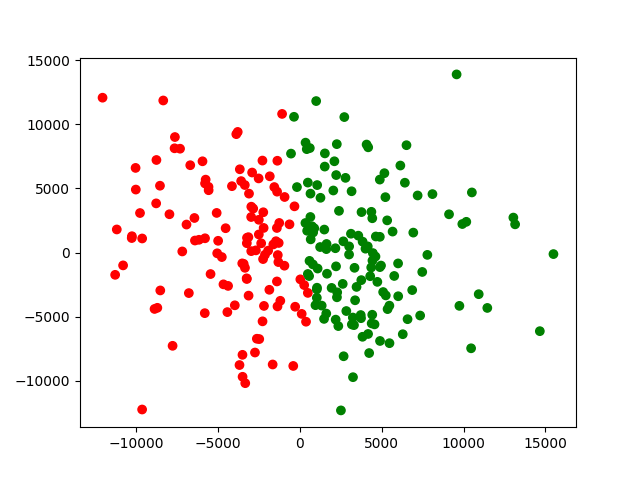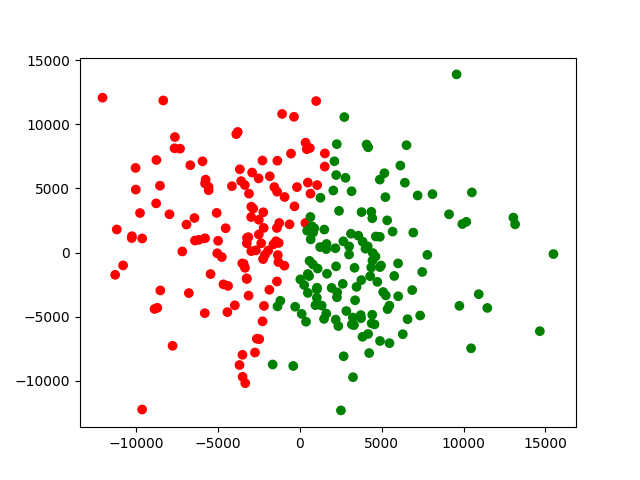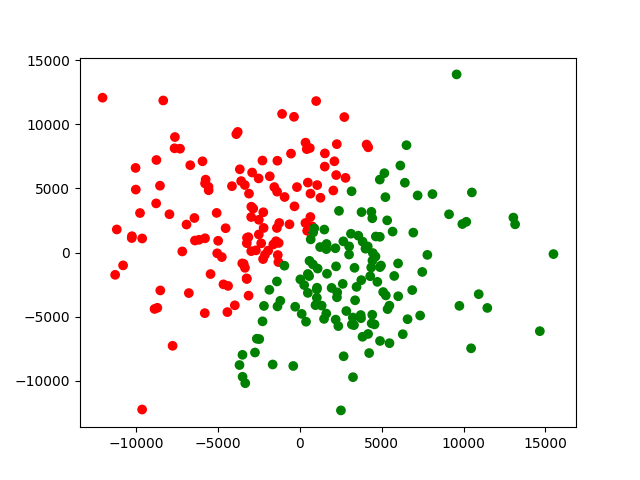
我们看到，开始还是随机是混合散点，但是k-均值算法可以很快就完成聚类。上面的图片的迭代十次的情况。

下面的代码对应的是处理指标个数为2的数据，分成两类，对应G1、G2，所以实现起来比较简单，但是却不具普遍性，一旦更改聚类个数或是数据不是二维的，代码就又要重新修改。

import numpy as np
def distance(x,y):return np.sqrt((x[0]-y[0])**2+(x[1]-y[1])**2)
for i in range(10):'''循环10次'''print('the {} epoch'.format(i))m1=np.mean(G1,axis=0)m2=np.mean(G2,axis=0)g1=[];g2=[]for j in range(len(G1)):d1=distance(G1[j],m1)d2=distance(G1[j],m2)if d1<=d2:g1.append(G1[j])else:g2.append(G1[j])for j in range(len(G2)):d1=distance(G2[j],m1)d2=distance(G2[j],m2)if d1<=d2:g1.append(G2[j])else:g2.append(G2[j])G1=g1;G2=g2