题型:
1.思维题/杂题:数学公式,分析题意,找规律
2.BFS/DFS:广搜(递归实现),深搜(deque实现)
3.简单数论:模,素数(只需要判断到 int(sqrt(n))+1),gcd,lcm,快速幂(位运算移位操作),大数分解(分解为质数的乘积)
4.简单图论:最短路(一对多(Dijstra,临接表,矩阵实现),多对多(Floyd,矩阵实现)),最小生成树(并查集实现)
5.简单字符串处理:最好转为列表操作
6.DP:线性DP,最长公共子序列,0/1背包问题,最长连续字符串,最大递增子串
7.基本算法:二分,贪心,组合,排列,前缀和,差分
8.基本数据结构:队列,集合,字典,字符串,列表,栈,树
9.常用模块:math,datetime,sys中的设置最大递归深度(sys.setrecursionlimit(3000000)),collections.deque(队列),itertools.combinations(list,n)(组合),itertools.permutations(list,n)(排列) heapq(小顶堆)
目录
题型:
模板回顾:
1.DFS代码框架(搜图建议↓为x方向,→为y方向)(找有多少条路径)
搜路径模板
搜索组合模板
BFS+DFS
2.BFS逐层搜索(找最短路径)
搜索模板
BFS搜索示例 (通过set()去重)
3.并查集(连通子图,最小生成树)
4.DP动态规划 ( 完全背包 http://t.csdn.cn/HnkGN)( http://t.csdn.cn/jSSby)
0/1背包问题:
最长公共子序列
最长递增子序列(LIS)
编辑距离(字符串转换)
5.数论
LCM和GCD
快速幂
矩阵乘法
埃式筛
大数分解(质因数分解)
6.组合数学
加法原理
鸽巢原理
杨辉三角编辑
7.计算几何
点积
叉积
点跟直线关系
8.图论算法(图论章节http://t.csdn.cn/pitI6)
存边方式
Floyd算法
Dijstra算法
Bellman-ford算法
9.常用库
10.前缀和、差分
模板回顾:
1.DFS代码框架(搜图建议↓为x方向,→为y方向)(找有多少条路径)
(BFS章节:http://t.csdn.cn/iv8UO)

标记数组,记录数组,全局变量ans
搜路径模板

搜索组合模板

BFS+DFS
import sys #设置递归深度
import collections #队列
import itertools # 排列组合
import heapq
sys.setrecursionlimit(100000)s="01010101001011001001010110010110100100001000101010 \
10000001100111010111010001000110111010101101111000"vis=[[0]*60 for _ in range(60)] # 标记是否访问过
fa=[['']*60 for _ in range(60)] # 记录父结点
flag=['D','L','R','U'] # ↓x → y
##a = list(s.split(' '))
##print(a)
##ss=[]
##for i in s: #转为2维列表
## ss.append(i)
##print(ss)
ss=[]
for i in range(30):ss.append(list(map(int,input())))def dfs(x,y): # 通过DFS遍历找路径if x==0 and y==0:returnif fa[x][y]=='D':dfs(x-1,y)if fa[x][y] =='L': dfs(x,y+1)if fa[x][y] =='R': dfs(x,y-1)if fa[x][y] =='U': dfs(x+1,y)print(fa[x][y],end='')def bfs(x,y):global faglobal visdeque=collections.deque()walk=[[1,0],[0,-1],[0,1],[-1,0]] # 下,左,右,上vis[x][y]=1deque.append((0,0)) # 添加进队列while deque:x,y=deque.popleft()#print(x,y)if x==29 and y==49:print("找到终点!!")breakfor index in range(4):dx,dy=walk[index]nx=x+dx;ny=y+dyif 0<=nx<=29 and 0<=ny<=49 :if vis[nx][ny]==0 and ss[nx][ny]==0: # 坐标合法且没有走过vis[nx][ny]=1deque.append((nx,ny))fa[nx][ny]=flag[index]bfs(0,0)
dfs(29,49)用栈记录路径,即在保护现场是入栈,恢复现场时出栈。
2.BFS逐层搜索(找最短路径)
(BFS章节:http://t.csdn.cn/G1kgx)
搜索模板

BFS搜索示例 (通过set()去重)
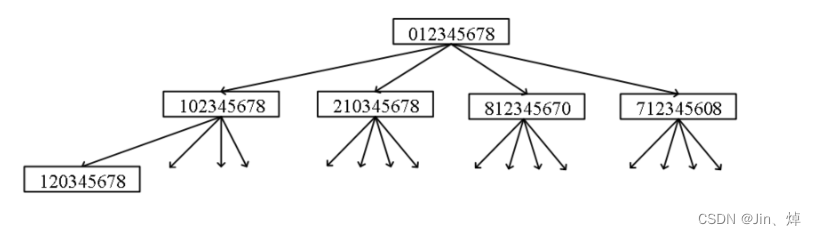
3.并查集(连通子图,最小生成树)

4.DP动态规划 ( 完全背包 http://t.csdn.cn/HnkGN)( http://t.csdn.cn/jSSby)
0/1背包问题:
def solve(N,C): # 从左到右,从上到下 (先种类,再体积)for i in range(1,N+1): # N种物品,先1种,再2种......for j in range(1,C+1): # 当前背包体积if c[i]>j : dp[i][j] = dp[i-1][j] # 新增的第i种物品的体积大于背包重量,只有不选,继承上一个选择else: dp[i][j] = max(dp[i-1][j-c[i]]+w[i],dp[i-1][j]) # 装或者不装,找最大值return dp[N][C]
N,C= map(int,input().split())
n=3010
dp = [[0]*n for i in range(n)] # 初始化dp数组,预留更大空间
c=[0]*n # 记录体积
w=[0]*n # 记录价值
for i in range(1,N+1): #读入N种物品的价值和体积c[i],w[i] = map(int,input().split())
print(solve(N,C))最长公共子序列
n,m = map(int,input().split()) # B n个元素 A m个元素
a = [0] + list(map(int,input().split()))
b = [0] + list(map(int,input().split()))
dp = [[0]*(m+1) for _ in range(2)] # 注意这里是m,不是n
now = 0 ;old = 1
for i in range(1,n+1):now,old = old,nowfor j in range(1,m+1):dp[now][j] = max(dp[now][j-1],dp[old][j])if a[i]==b[j]: # 相同的元素dp[now][j] = max(dp[now][j],dp[old][j-1]+1)
print(dp[now][m])最长递增子序列(LIS)

N =int(input()) # 对手个数
a = [0]+[int(i) for i in input().split()] # 记录对手战力值
dp = [0]*(N+1) # 记录以第i个数为结尾的最长递增子序列
dp[1]=1
for i in range(2,N+1): # 从2-N循环for j in range(1,i): # 查找前面的比a[i]小的if a[j]<a[i] and dp[j]>dp[i]: #找到小的同时给他赋值max(dp[j])dp[i]=dp[j]dp[i]+=1 # 加1,即本身编辑距离(字符串转换)



5.数论
LCM和GCD


快速幂
位运算
通过 n&1=True,则n最低位就是1
n>>,n右移动def fast(a,n,mod):ans=1a%=mod # 提升运算效率,Python不用担心大数月越界问题while(n)>0:if n&1 :ans=(a*ans)%mod#a=a*a # 翻倍a=(a*a)%mod # 翻倍n=n>>1 # 右移一位
a,b,mod = map(int,input().split())
print(fast(a,b,mod))矩阵乘法

埃式筛

大数分解(质因数分解)
import sys #设置递归深度
import collections #队列
import itertools # 排列组合
import heapq #小顶堆
import math
sys.setrecursionlimit(300000)#对一个数进行大数分解
ans=0
n=int(input())
for i in range(2,int(math.sqrt(n))+1):if n%i==0: #发现质数ans+=1#print(i) # 打印质数约数while n%i==0: # 消除这个质数n=n//i
if n>1:#print(n) # 打印质数约数ans+=1
print(ans)6.组合数学
加法原理

鸽巢原理

杨辉三角
import os
import sys# 骗分写法
n=int(input())
a=[[1],[1,1]]
for i in range(1,500): # 50-1+2行b=[]temp=0for j in range(i): # 根据上一行i计算temp=a[i][j]+a[i][j+1]b.append(temp)a.append([1]+b+[1])
# print(a)
b=[]
for i in range(501): #进行队列拼接b=b+a[i]
print(b.index(n)+1) # 直接通过队列值找索引import os
import sys# 请在此输入您的代码
n=[0,1,1,1,1,2,1]
#n=[[0],[1,1],[1,2,1]]
last=[1,2,1]
for i in range(50):new=[]for a,b in zip(last+[0],[0]+last):new.append(a+b)n.append(new)last=newm=int(input())
print(n.index(m))
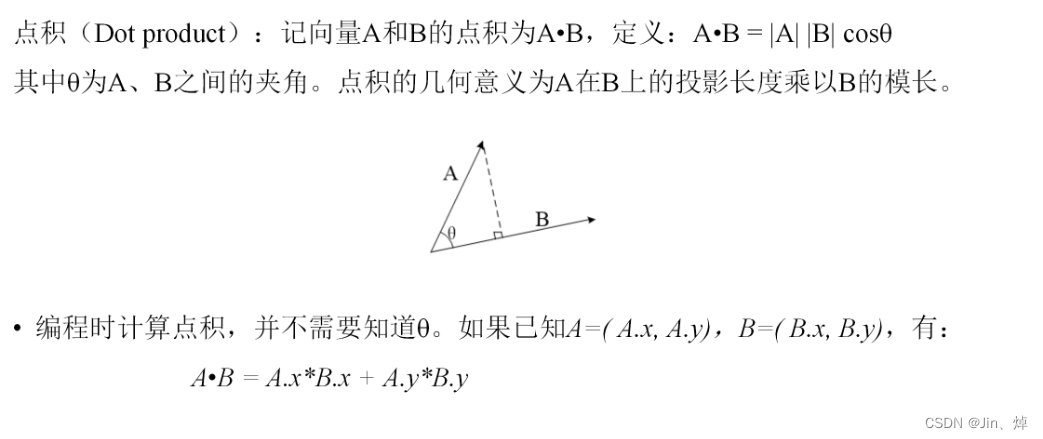
7.计算几何
点积

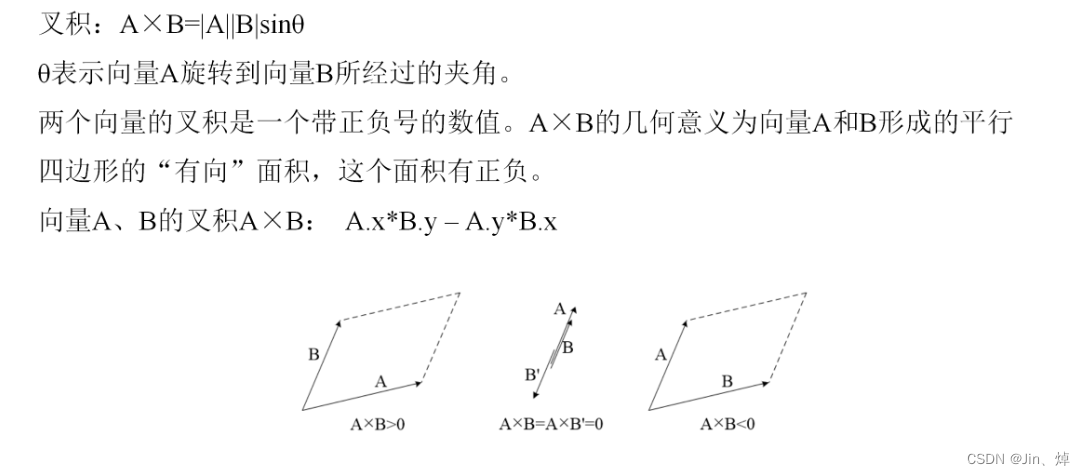
叉积

点跟直线关系



8.图论算法(图论章节http://t.csdn.cn/pitI6)
存边方式
数组存边

临接矩阵
 邻接表
邻接表

Floyd算法

import os
import sys# 请在此输入您的代码
#floyd算法,多对多def floyd():global dpfor i in range(1,n+1):for j in range(1,n+1):for k in range(1,n+1):dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j])n,m,q = map(int,input().split())
inf=2**120
dp=[[inf]*(n+1) for i in range(n+1)]
choice=[]
for i in range(m):u,v,w=map(int,input().split())dp[u][v]=wdp[v][u]=w
for i in range(q):s,d = map(int,input().split())choice.append((s,d))
floyd()
for s,d in choice:if dp[s][d]!=inf:print(dp[s][d])continueprint(-1)Dijstra算法
import heapq # 导入堆
def dij(s):done=[0 for i in range(n+1)] # 记录是否处理过hp=[] #堆dis[s]=0heapq.heappush(hp,(0,s)) #入堆,小顶堆while hp:u=heapq.heappop(hp)[1] #出堆元素结点if done[u]: #当前结点处理过continuedone[u]=1for i in range(len(G[u])): #遍历当前结点的邻居v,w =G[u][i]if done[v]:continuedis[v]=min(dis[v],dis[u]+w) # 更新当前结点邻居的最短路径heapq.heappush(hp,(dis[v],v))n,m = map(int,input().split())#
s=1 # 从1开始访问
G=[[]for i in range(n+1)] #邻接表存储
inf = 2**50
dis = [inf]*(n+1) #存储距离
for i in range(m):# 存边,这里是单向边u,v,w = map(int,input().split())G[u].append((v,w)) #记录结点u的邻居和边长dij(s)
for i in range(1,n+1):if dis[i]==inf:print("-1",end=' ')else:print(dis[i],end=' ')import sys #设置递归深度
import collections #队列
import itertools # 排列组合
import heapq #小顶堆
import math
sys.setrecursionlimit(300000)def dij():dist[1]=0 #很重要for _ in range(n-1): # 还有n-1个点没有遍历t=-1for j in range(1,n+1):if st[j]==0 and (t==-1 or dist[t]>dist[j]): #找到没处理过得最小距离点t=jfor j in range(1,n+1):dist[j]=min(dist[j],dist[t]+gra[t][j]) # t-j的距离,找最小值st[t]=1 # 标记处理过return dist[n]n,m=map(int,input().split())#下标全部转为从1开始
stay=[0]+list(map(int,input().split()))
stay[n]=0
gra = [[float('inf')] * (n+1) for _ in range(n+1)]
dist = [float('inf')] * (n+1)
st=[0]*(n+1) # 标志是否处理for i in range(m):u,v,w=map(int,input().split()) #这里重构图gra[u][v]=stay[v]+wgra[v][u]=stay[u]+wprint(dij())Bellman-ford算法
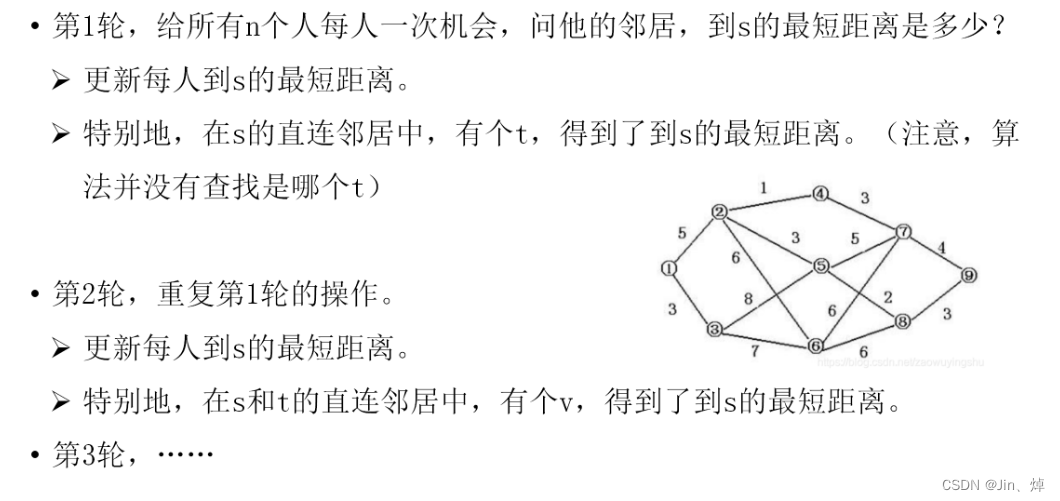
n,m=map(int,input().split())
t=[0]+list(map(int,input().split()))
e=[] #简单的数组存边for i in range(1,m+1):a,b,c = map(int,input().split())e.append([a,b,c]) # 双向边e.append([b,a,c])dist=[2**50]*(n+1)
dist[1]=0for k in range(1,n+1): # 遍历每个点,n个点,执行n轮问路for a,b,c in e: # 检查每条边,每一轮问路,检查所有边res=t[b]if b==n:res=0dist[b]=min(dist[b],dist[a]+c+res) # 更新路径长度print(dist[n])9.常用库
math
datetime datetime.date() date.days() date.timedelta
sys中的设置最大递归深度(sys.setrecursionlimit(3000000)) sys.exit()
collections.deque(队列)
itertools.combinations(list,n)(组合),itertools.permutations(list,n)(排列)
heapq(小顶堆) heapq.heappush(list,(0,s)) # 将list堆化,向list添加元素(0,s)
10.前缀和、差分
http://t.csdn.cn/rQs6M