1 欧拉角概念

• 百度百科：欧拉角，用来确定定点转动刚体位置的3个一组独立角参量，欧拉角由章动角θ、旋进角（即进动角）ψ和自转角Φ组成。欧拉角为欧拉首先提出而得名。
• 维基百科：Euler angles，莱昂哈德·欧拉用欧拉角来描述刚体在三维欧几里得空间的取向。对于任何参考系，一个刚体的取向，是依照顺序，从这参考系，做三个欧拉角的旋转而设定的。所以，刚体的取向可以用三个基本旋转矩阵来决定。换句话说，任何关于刚体旋转的旋转矩阵是由三个基本旋转矩阵复合而成的。

2 欧拉角定义

对于在三维空间里的一个参考系，任何坐标系的取向，都可以用三个欧拉角来表现。参考系又称为实验室参考系，是静止不动的，而坐标系则固定于刚体，随着刚体的旋转而旋转。
以下规定：XYZ坐标轴是旋转的刚体坐标轴；而xyz坐标轴是静止不动的实验室参考轴。
参考下图，坐标系XYZ原与参考系xyz重合，旋转后，称xy平面与XY平面的交线为交点线，用英文字母N代表。zXZ顺规的欧拉角可以静态地定义如下：

• α是x轴与交点线的夹角；
• β是z轴与Z轴的夹角；
• γ是交点线与X轴的夹角。
  

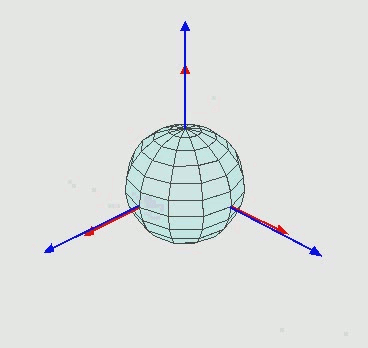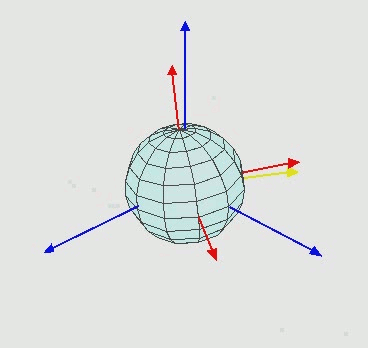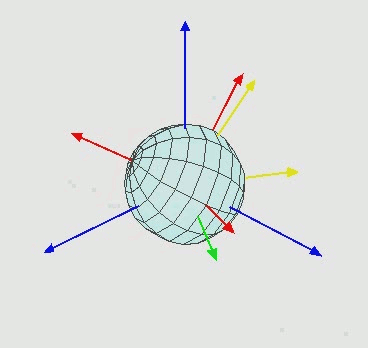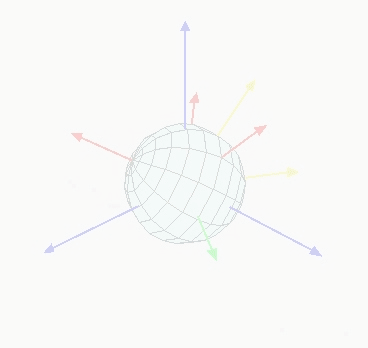
右图用动画描述了旋转的过程：即第一绕z轴旋转α，第二绕交点线（即X轴旋转后的轴）旋转β，第三绕Z轴旋转γ.
因此，此过程可分解为三个基本的旋转，从左到右依次代表绕着z轴的旋转、绕着交点线的旋转、绕着Z轴的旋转。即其旋转矩阵为
$$\begin{gathered} R=R_Z(\alpha )R_X(\beta )R_z(\gamma )=\left[\begin{array}{ccc}cos\alpha & -sin\alpha & 0\\ sin\alpha & cos\alpha & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& cos\beta & -sin\beta \\ 0& sin\beta & cos\beta \end{array}\right]\left[\begin{array}{ccc}cos\gamma & -sin\gamma & 0\\ sin\gamma & cos\gamma & 0\\ 0& 0& 1\end{array}\right] \\ =R_z^{-1}(\gamma )R_X^{-1}(\beta )R_Z^{-1}(\alpha )=\left[\begin{array}{ccc}cos\gamma & sin\gamma & 0\\ -sin\gamma & cos\gamma & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& cos\beta & sin\beta \\ 0& -sin\beta & cos\beta \end{array}\right]\left[\begin{array}{ccc}cos\alpha & sin\alpha & 0\\ -sin\alpha & cos\alpha & 0\\ 0& 0& 1\end{array}\right] \end{gathered}$$
合法的欧拉角组中，唯一的限制是，任何两个连续的旋转，必须绕着不同的转动轴旋转。因此，一共有12种顺规，分别被划分为两类：

• 经典欧拉角：z-x-z, x-y-x, y-z-y, z-y-z, x-z-x, y-x-y
• 泰特-布莱恩角（Tait–Bryan angles）：x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z

可以看出两者的区别是：经典欧拉角的第一个旋转角度和第三个旋转角度都是围绕同一个轴的（例如z-x-z,或者 z-x’-z’‘），而Tait-Bryan角使用三个轴上的旋转角度去表示（例如 x-y-z或者x-y’-z’‘）。
泰特-布莱恩角（Tait–Bryan angles）又常称为：yaw（偏航，绕z旋转）-pitch（俯仰，绕y’旋转）-roll（翻滚，绕x’'旋转)

3 欧拉角的计算

同样的一个旋转，按旋转的坐标系又可分为内旋和外旋：
定义A：内旋，绕着XYZ坐标轴旋转，旋转轴是动态的：最初，两个坐标系统xyz与XYZ的坐标轴是重合的。开始先绕着Z轴旋转α角值。然后，绕着X轴旋转β角值。最后，绕着Z轴作角值γ的旋转。上面动态图表示的就是这个内旋过程。实际上，内旋就是以上的欧拉角静态定义
内旋的旋转矩阵：
$$R=R_Z(\alpha )R_X(\beta )R_Z(\gamma )$$
内旋按顺序右乘。
定义B：外旋，绕着xyz坐标轴旋转，旋转轴始终不变：最初，两个坐标系统xyz与XYZ的坐标轴是重合的。开始先绕着z轴旋转γ角值。然后，绕着x轴旋转 β角值。最后，绕着z轴作角值α的旋转。
外旋的旋转矩阵：
$$R=R_z(\alpha )R_x(\beta )R_z(\gamma )$$
外旋按顺序左乘。

可以证明，以上定义A和定义B两者是等效的。
（原证明方法存在疑义，已移除，谢谢热心读者指点）。

4 万向锁

万向锁（Gimbal lock）是在使用动态欧拉角表示三维物体的旋转时出现的问题。一旦选择±90°作为pitch角，就会导致第一次旋转和第三次旋转等价，整个旋转表示系统被限制在只能绕竖直轴旋转，丢失了一个表示维度。

参考

https://blog.csdn.net/qq_38288618/article/details/77195271
https://blog.csdn.net/qq_21834027/article/details/85144454