• 问题 1 :对这些玻璃文物的表面风化与其玻璃类型、纹饰和颜色的关系进行分析；结合玻璃的类型，分析文物样品表面有无风化化学成分含量的统计规律，并根据风化点检测数据，预测其风化前的化学成分含量。
• 问题 2 :依据附件数据分析高钾玻璃、铅钡玻璃的分类规律；对于每个类别选择合适的化学成分对其进行亚类划分，给出具体的划分方法及划分结果，并对分类结果的合理性和敏感性进行分析。
• 问题 3 :对附件表单 3 中未知类别玻璃文物的化学成分进行分析，鉴别其所属类型，并对分类结果的敏感性进行分析。
• 问题 4 :针对不同类别的玻璃文物样品，分析其化学成分之间的关联关系，并比较不同类别之间的化学成分关联关系的差异性。

1、参赛感受

本人作为一个建模新手参加了22年的数模国赛，由于AB题都是物理题，最终我们团队选择了C题，在参赛过程中，主要担任了建模手和编程手，因为我是一名计算机科班生，学了很多编程语言，但自己平时都是以python为第一语言，c++为第二语言，为了不增加自己的学习压力，就没有深入学习matlab这门语言，而且相对于科班生来说，python语言使用价值远远大于matlab，所以我选择了python作为建模语言，后续我也会将自己备赛过程中，使用python进行数学建模的相关资料和代码进行分享，本次我将这次的参赛思路进行分享，本人建模新手，思路不佳还请大家见谅。

2、问题一

首先我们将问题一划分为以下三个小问：

1. 对玻璃文物的三个数据特征与表面是否风化的关系进行分析。
2. 并结合玻璃类型总结出玻璃表面化学成分含量的统计规律。
3. 预测风化文物在风化前的化学成分组成。

2.1、关系分析

方差分析是通过数据分析找出对该事物有显著影响的因素， 各因素之间的交互作用，以及显著影响因素的最佳水平等。
所以，我们构建玻璃类型、纹饰、颜色特征与表面风化关系模型：首先对表单一中的数据进行数据预处理，即采用多重插补法将缺失值补全，并进行深层次的数据挖掘。再探讨玻璃类型、纹饰、和颜色与表面是否风化之间的关系，探究三种特征是否对文物表面是否风化产生显著性影响。

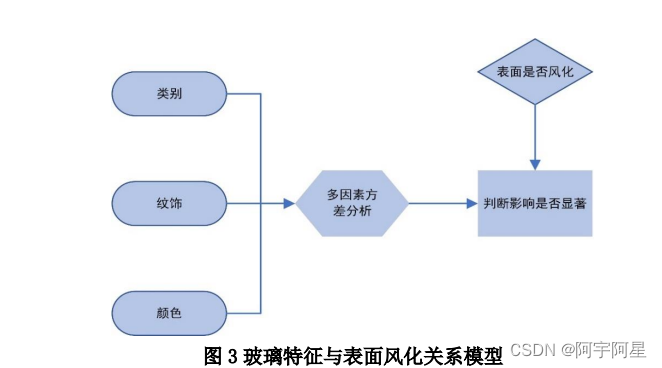
2.1.1、模型求解

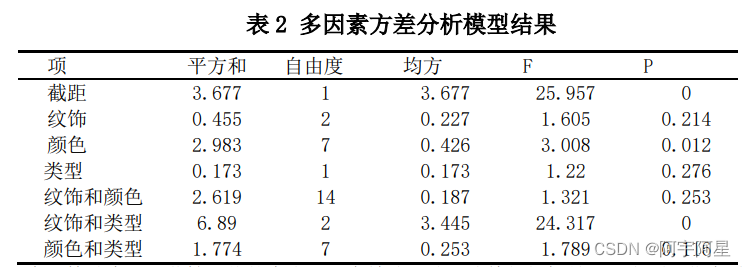
在 F 检验中，显著性 P 值的大小可以有效地反映出该特征指标是否对表面风化有重要影响，以及是否存在主效应，在一定范围内，P 值越小，说明该因素对表面风化影响的显著性越强，存在主效应。具体分析结果如下：
对于变量：纹饰，从 F 检验的结果分析可以得到，显著性 P 值为 0.214，水平上不呈现显著性，对表面风化没有显著性影响，不存在主效应。
对于变量：颜色，从 F 检验的结果分析可以得到，显著性 P 值为 0.012，水平上呈现显著性，对表面风化有显著性影响，存在主效应。
对于变量：类型，从 F 检验的结果分析可以得到，显著性 P 值为 0.276，水平上不呈现显著性，对表面风化没有显著性影响，不存在主效应。
对于交互项纹饰和颜色，从 F 检验的结果分析可以得到，显著性 P 值为 0.253，水平上不呈现显著性，对表面风化没有显著性影响，不存在交互作用。
对于交互项纹饰和类型，从 F 检验的结果分析可以得到，显著性 P 值为 0，水平上呈现显著性，对表面风化有显著性影响，存在交互作用。
对于交互项颜色和类型，从 F 检验的结果分析可以得到，显著性 P 值为 0.116，水平上不呈现显著性，对 Q5-表面风化没有显著性影响，不存在交互作用。

2.2、统计规律

我们按照玻璃类型进行划分数据，再继续按照是否风化、纹绣等进行划分数据，对比观察玻璃表面化学成分。


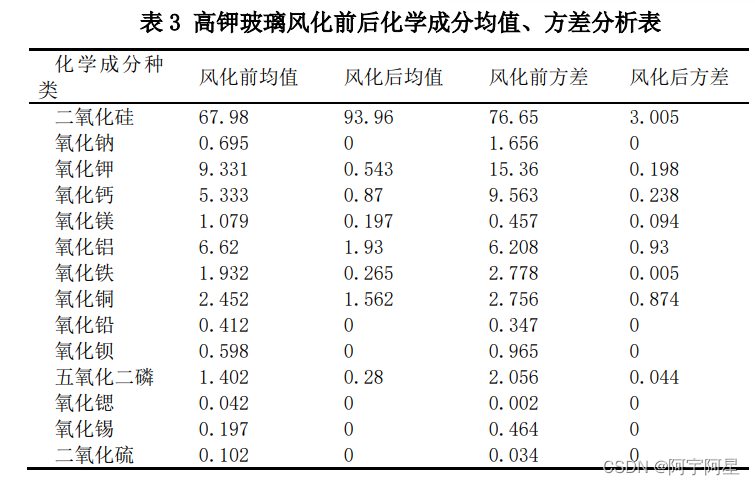
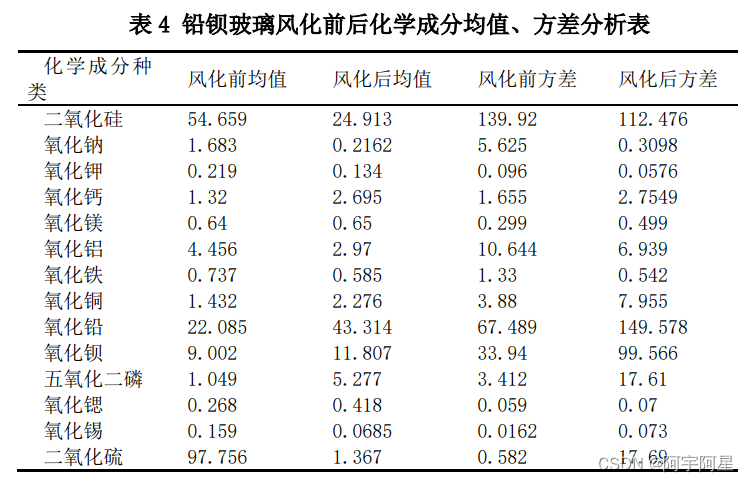
由上表所知，高钾玻璃文物风化后大多数化学成分会减少，而铅钡玻璃文物风化后大多数化学成分基本保持相对平稳；高钾玻璃文物风化后，同一类型物品化学成分的方差较小，而铅钡玻璃文物风化后，同一类型物品化学成分的方差较大。

2.3、成分预测

风化前化学成分的预测：通过对数据的深入挖掘与相关性分析，我们发现纹饰、类型、颜色三类指标对表面分化的影响显著性之和占比高达 99.7%，关系极其密切，相关性非常高，因此我们可近似认为若两份玻璃样品纹饰、类型、颜色三者指标相同，两份样品的化学组成成分相同，基于上述分析，可以预测出文物风化点风化前的化学组成成分。

3、问题二

问题二要求分析高钾玻璃与铅钡玻璃的分类规律，并在此基础上求出对每个类别合适化学成分的亚类划分方法与结果，并对其进行合理性与敏感性分析。本问题思路主要分为以下五步：
（1）数据标准化：本文首先对采样点的化学成分数据取平均值中心化，再按照数据的标准差进行缩放，得到以 0 为均值，方差为 1 的正态分布。
（2）降低文物采样点化学成分的维度：本文先对标准化的数据求解出相关系数矩阵，再计算出相关系数矩阵 的特征值与对应的标准正交化特征向量，最后求解出主成分的贡献率，按照累积贡献率选取前三个主成分，降低了表单化学成分维度。
（3）提炼出高钾玻璃与铅钡玻璃的分类规律：在上述工作的基础上，首先以排序得到的主要成分为决策树的判断特征，接着从根节点出发选择信息增益最大的特征为节点特征，生成新的子节点，多次迭代生成，最后对决策树剪枝处理得到两类玻璃的分类规律。
（4）总结出亚类划分方法：根据表单数据以及查阅资料，本文对已风化的玻璃进行亚类分析，运用 K-means 聚类算法，首先将 k 定为 2（聚类成两类：严重风化，一般风化），随机选定初始点为质心，计算每一个样本与质心之间的欧式距离，将样本点聚到最相似的类中，反复迭代，直到质心不再改变，最终确定每个样本所属的亚类。
（5）敏感性分析：通过控制变量法，探究模型某参数改变，其他参数不变情况下，模型准确率的变化；添加数据扰动处理，即数据的合理放缩，对模型敏感性分析研究。

3.1、分类规律模型

首先对表单二的化学成分比例数据采用 Z-Score 算法，使其标准化。再对表单二中各化学成分比例运用主成分分析算法，筛选出其中累计贡献度大于 90%的化学成分比例指标，达到降维的目的。在 14 种主成分中筛选出累积贡献率 90%的主成分，按贡献度依次对排序结果分别为：第一主成分、第二主成分、第三主成分。
根据主成分分析结果，各主成分贡献度占比母子饼状图为：

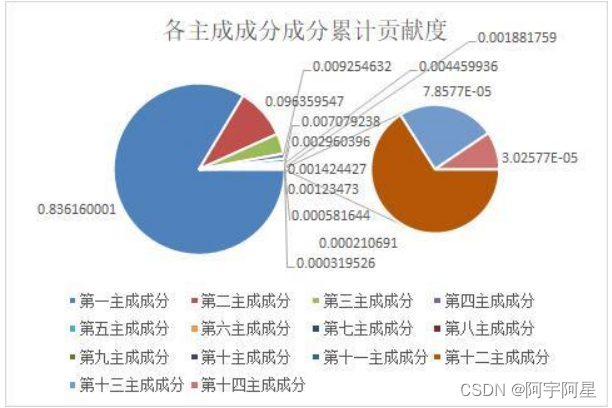
3.1.1、分类规律

通过决策树对其主成分氧化钾(K2O)进行第一节点判断，若含钾则继续下一节点，若不含钾则为铅钡玻璃，在下一节点对氧化钠(Na2O)含量是否达到预设阈值进行判定，若达到阈值，则说明其虽有钾，但其含量较低，因此判定为铅钡玻璃，若纳含量低于阈值，则说明钾含量达标，为高钾玻璃。

3.2、亚分类模型

本文对附件中按类型筛选后的数据再按照其风化程度进行亚分类，将高钾玻璃和铅钡玻璃按照严重风化和一般风化两类进行分析，分别对已风化的高钾玻璃和铅钡玻璃进行 k-means 聚类，然后根据附件中已知严重风化点的所在类别，进行类型判别，利用 python 进行求解。

3.3、模型检验与敏感性分析

3.3.1、决策树模型检验

Kappa 系数可以用来对有监督学习的结果的精度进行评价，本文采用其对决策树模型的分类结果进行精度评价。
$$Kappa=\frac{p_0-p_e}{1-p_e}$$
解得 Kappa=0.8374>0.81，可以证明决策树模型的分类几乎完全一致，即精度非常高。

3.3.2、K-means模型检验

采用肘部对 K-means 聚类的最佳 k 值进行检验，随着类别数选取的增加，SSE 的趋势在通过拐点后，即最佳 k 值，SSE 下降趋势将会变缓。

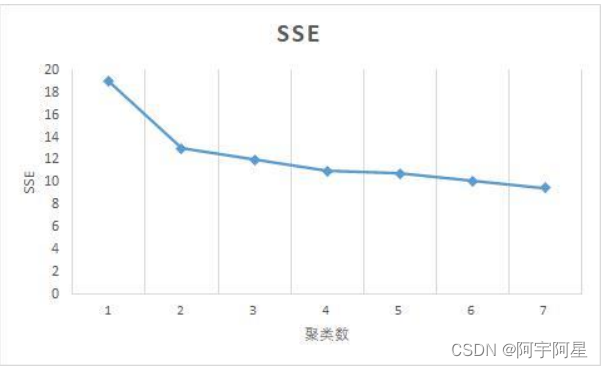
由图可知，当 K=2 过后，SSE 下降趋势逐渐平缓，所以问题二的亚分类数量最佳为 2，即模型对 K 值的设定合理(严重风化类和一般风化类)。

3.3.3、模型敏感性分析

我们通过对原始数据进行小扰动处理，即进行合理放缩，进行敏感性分析，对处理后的数据的预测结果与原始数据的预测结果进行比对，结果如下所示：

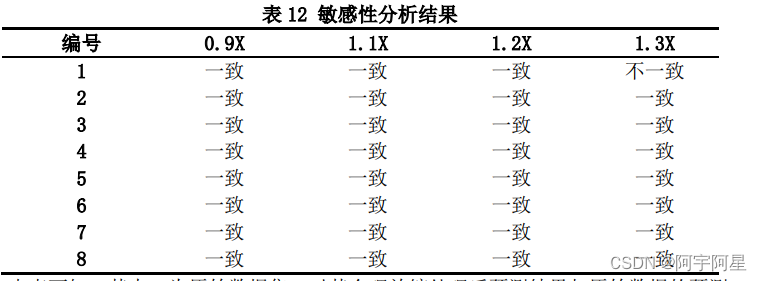
由表可知，其中 X 为原始数据集，对其合理放缩处理后预测结果与原始数据的预测结果几乎一致，准确率达 96.875%，说明模型的鲁棒性较好，准确率较高。

4、问题三

问题三要求对表单 3 中未知类别的玻璃文物进行类别分类。本题求解步骤分以下两步：在第二问的基础上首先综合运用问题二的决策树模型对未知类别玻璃分类为高钾玻璃或者铅钡玻璃，再用 K-means 聚类算法来对上一步分好的大类进行亚类划分。本文在问题二模型结论的基础上再次使用主成分分析法，鉴别出未知玻璃大类。接着使用 K-means 聚类分析，选择出合适的亚分类指标作为亚类分析的判据。利用 python 编程求解上述模型，得到 8 份未知玻璃文物的样品分类结果如下表：

敏感性分析思路同问题二，这里就不在重述了，感兴趣的同学翻看问题二的敏感性分析方法，进行套用。

5、问题四

问题四要求针对高钾玻璃与铅钡玻璃样品分类，分析其化学成分之间的关系。本文考虑利用皮尔逊系数构建相关系数矩阵来分析化学成分之间的关系。问题四的整体思路流程图如下：

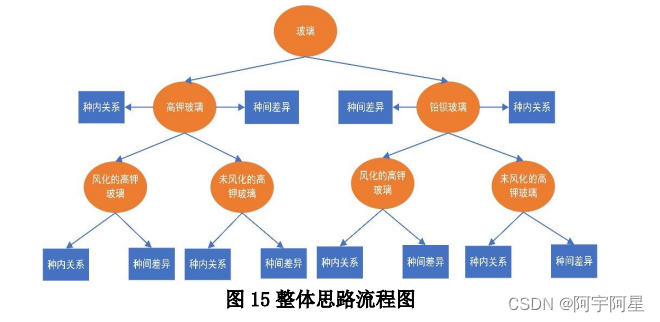
我们可以发现：高钾玻璃化学成分之间的相关性与铅钡玻璃化学成分之间的相关性存在显著性差异，而且对高钾玻璃和铅钡玻璃再按表面风化进行分类分析，对比发现表面风化也会对化学成分之间的相关性造成影响，所以不同类别之间的化学成分关系有着显著差异。

6、参考文献

[1]司守奎，孙兆亮.数学建模算法与应用[M].北京，国防工业出版社，2017
[2]魏晓，文雪峰，杨瑞东. 贵州从江县大融砖厂新元古界浅变质岩现代风化壳剖面中微量元素分布特征与相关性分析[J]. 地球与环境. 2010,38(03)
[3]虞颖，孟彦菊.中国 31 个主要城市空气质量的聚类分析和主成分分析[J]. 科技和产业. 2022,22(05)
[4]钟琪，罗津，齐述华.随机森林分类算法提取橘果园的样本数量敏感性分析[J].江西学.019,37(05)
[5]何坤龙,赵伟,刘晓辉,刘蛟.云雾覆盖下地表温度重建机器学习模型的训练集敏感性分析[J].遥感学报,2021,25(08):1722-1734.

7、完整论文

玻璃文物化学成分分析与鉴别