目录
一、二叉查找树概念
二、结点内部类代码实现:
三、二叉查找树的插入原理编辑
四、遍历的方式(中序遍历):
五、二叉查找树实现指定值删除对应的结点
六、main方法测试
一、二叉查找树概念
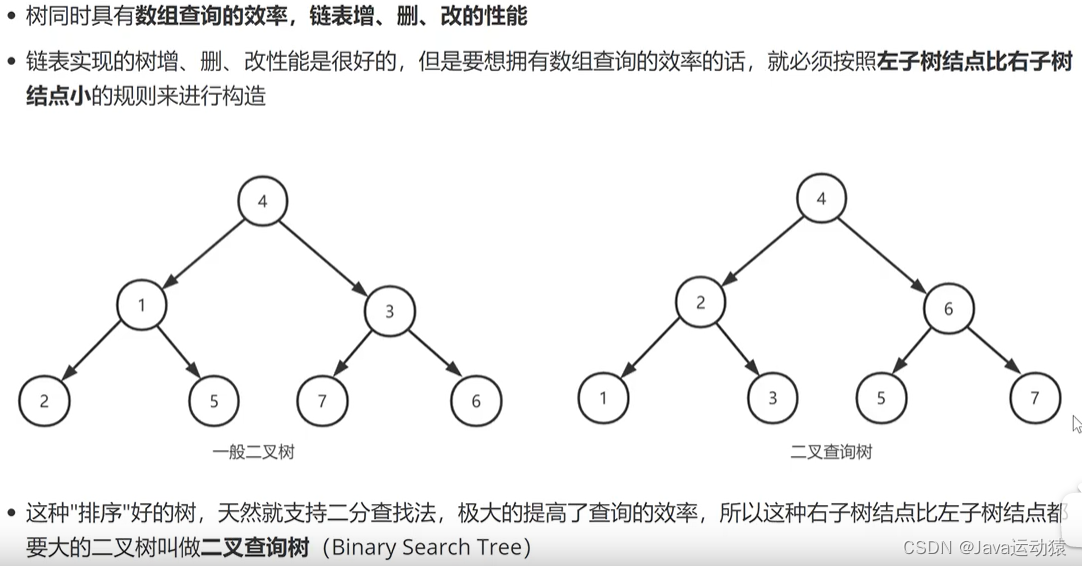
二、结点内部类代码实现:
public class BinarySearchTree {//写一个结点内部类public static class Node{int value;Node left;Node right;public Node(int value){this.value = value;}}//先定义一个根节点Node root;
} 三、二叉查找树的插入原理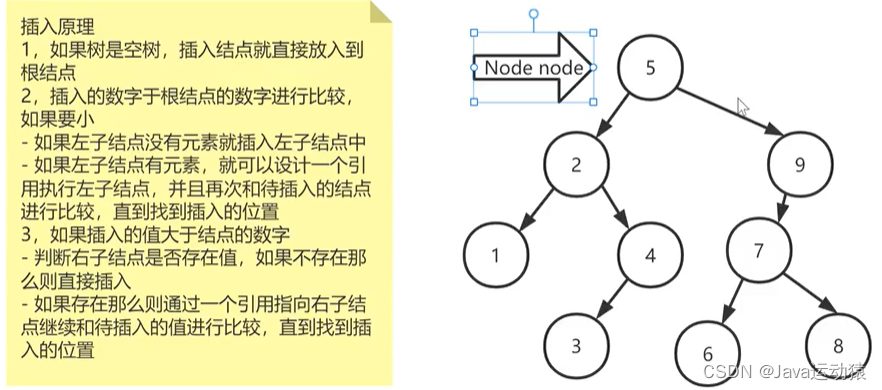
//写一个插入类public void insert(int value){//如果树为null,则直接插入在根节点上if (root == null){root = new Node(value);}//声明一个游标结点,开始指向根节点Node node = root;//如果树不为null,则比较插入的值与根节点的大小,小放左边大放右边while(true){if (value < node.value){//如果root.left为null,则直接插入到root.left中if (node.left == null){node.left = new Node(value);break;}else{//将游标指向左子节点node = node.left;}}else {if (node.right ==null){node.right = new Node(value);break;}else {//将游标指向右子节点node = node.right;}}}}四、遍历的方式(中序遍历):
1.通过中序遍历就可以将二叉查找树进行顺序输出。
2.中序遍历的特征:左、根、右
通过中序遍历,刚好可以把二叉查找树从小到大进行遍历输出。
//实现中序遍历public void midTraversal(Node node){if (node == null){return;}//先遍历左子节点midTraversal(node.left);//打印根节点System.out.print(node.value+" ");//再遍历右子节点midTraversal(node.right);}五、二叉查找树实现指定值删除对应的结点
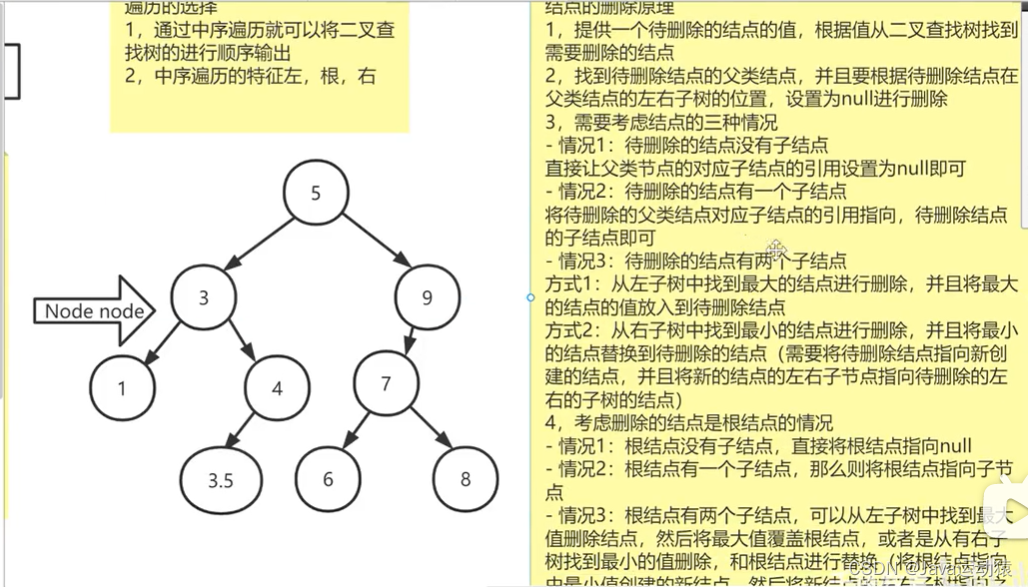
public static final int LEFT = 0;public static final int RIGHT = 1;//实现删除指定结点public void deleteNode(int value){//定义一个游标指针Node node = root;//定义一个目标结点Node target = null;//定义一个target的父类结点Node parent = null;//定义一个结点类型,左结点为0,右节点为1int nodeType = 0;//先进行查找目标元素while (node != null){//当node等于null的时候说明树中没有目标结点if (node.value == value){//找到结点了target = node;break;}else if (value < node.value){parent = node;//先记录node的父节点node = node.left;//node往左下方遍历nodeType = LEFT;}else {parent = node;node = node.right;nodeType = RIGHT;}}//如果target为null,则表示树中没有此节点if (target == null){System.out.println("没有找到要删除的结点");}//删除结点的三种方式,原理有两种,一种是将父类结点的指针指向新的子节点,// 另一种是将一个子节点的值替换掉目标结点,同时删除那个替换的子节点。//1.如果结点是叶子结点,也就是没有子节点的情况if (target.left == null && target.right == null){//如果树只有一个根节点,删除根节点的情况if (parent == null){//将root设置为null即可root = null;return;}//判断目标的结点是左子节点还是右子节点if (nodeType == LEFT){parent.left = null;}else{parent.right = null;}}else if (target.left != null && target.right != null){//2.如果删除的结点有两个子节点的情况//这种情况下,我们可以选择目标结点的左子树中最大的结点替换目标结点,// 也可以选择右子树中最小的结点替换掉目标结点//从target的右子树中查找最小的值Node min = target.right;while (min.left != null){min = min.left;}//将右子树中最小的值的结点删除deleteNode(min.value);//将最小值覆盖到目标结点上,完成目标结点的删除target.value = min.value;}else{//如果删除的是根节点,且根节点只有一个子节点if (parent == null){if (target.left != null){root = target.left;}else {root = target.right;}return;}//3.如果删除的结点只有一个子节点的情况if (nodeType == LEFT){if (target.left != null){//将父类的子节点指向待删除子节点的左子节点parent.left = node.left;}else {//将父类的子节点指向待删除子节点的右子节点parent.left = node.right;}}else {if (target.left != null){//将父类的子节点指向待删除子节点的左子节点parent.right = node.left;}else {//将父类的子节点指向待删除子节点的右子节点parent.right = node.right;}}}}六、main方法测试
package Tree.BinarySearchTree;public class TestBinarySearchTree {public static void main(String[] args) {int[] arr2 = {5,2,1,4,3,9,7,6,8};BinarySearchTree bst2 = new BinarySearchTree();
// //将数组中的元素构造成二叉查询树for (int i = 0;i<arr2.length;i++){bst2.insert(arr2[i]);}//中序遍历bst2.midTraversal(bst2.root);//删除指定元素bst2.deleteNode(9);System.out.println();bst2.midTraversal(bst2.root);}
}