思维导图：

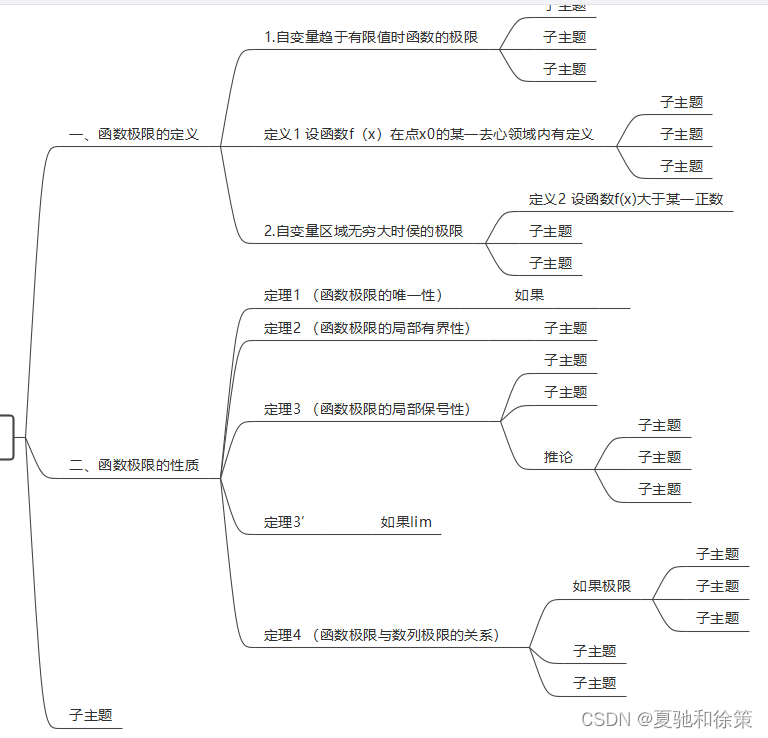
一 、函数极限的定义

因为数列111可看作自变量为n的的数：5，=/(口)，nEN.，所以，数列！士。1的
极限为a,就是:当自变量n取正整数而无限增大(即n一,∞)时,对应的两数值
rn)无限接近于确定的数。.把数列极限概念中的西数为/(，而自安量的变化过
程为n-∞0 等特殊性撒开，这样可以 出阿数城限的一-般概恐：在自空量的某个变
化过程中，如果对应的两数值无限接近于某个确定的数,那么这个确定的数就叫做
在这一变化过程中两数的极限．这个极限是与自变量的变化过程密切相关的,由于
自变量的变化过程不同，西数的极限就表现为不同的形式• 数列极限看作西数((几)
当n一∞时的极限，这里自变量的变化过程是n一∞.下面讲述自变量的变化过程
为其他情形时西数广(工)的极限，主要研究两种情形：
（1）自变量,任意地接近有限值x0,或者说趋于有限值x0,不(记作x一>x0)时，对应的西数值广(工)的变化情形；
（2）自变量，的绝对值lzl无限增大即哲丁无穷大(记作一∞)时,对应的
雨数值广(x）的变化情形

我的理解：

在数学中，函数极限是指当自变量趋近于某个值时，函数输出值的趋势和极限值的概念。更具体地说，给定一个函数f(x)，我们说f(x)在x趋近于a时的极限为L，如果对于任意给定的正数ε，存在另一个正数δ，使得当0<|x-a|<δ时，|f(x)-L|<ε。

这个定义可以解释为：当x在a附近，但不等于a时，f(x)趋近于L。也就是说，无论我们想让f(x)多接近L有多少，只要我们取得x足够接近a，就能够保证f(x)接近L，但不等于L。

这个定义有一些重要的性质。首先，如果函数的极限存在，那么它是唯一的。其次，如果函数在某个点处连续，那么该点的极限和函数值相等。最后，如果一个函数的极限不存在，那么它被称为发散。

函数极限是微积分和数学分析的重要概念，它在求导、积分和级数的计算中都有应用。了解函数极限的定义和性质对于学习这些主题是非常重要的。

要点：

函数极限的概念有以下几个要点：

趋近某个值：函数极限的定义中，自变量x必须趋近于某个特定的值a。这意味着我们要考虑函数在a的邻域内的行为，而不仅仅是在a处的函数值。(做题目尤其是选择题时要注意)
趋势和极限值：当自变量x趋近于a时，函数f(x)的输出值可以有多种趋势。极限L是当x趋近于a时，f(x)的趋势所达到的极限值。因此，L不一定是函数f(x)在a处的函数值。
精度和邻域：函数极限的定义中，要求对于任意正数ε，都存在另一个正数δ，使得当0<|x-a|<δ时，|f(x)-L|<ε。这意味着函数f(x)在a的邻域内必须足够接近极限值L，而且这个“足够接近”要求可以根据我们给定的精度ε来控制。
唯一性和连续性：如果函数在某个点处连续，那么该点的极限和函数值相等，即f(a) = lim_{x→a} f(x)。如果函数的极限存在，那么它是唯一的，也就是说，一个函数不能同时趋近于两个不同的极限。
这些要点对于理解函数极限的概念和计算函数极限非常重要。在实际应用中，我们需要利用这些要点来确定函数极限是否存在，以及如何计算函数极限。

1. 自变量趋于有限值时函数的极限

现在考虑自变量， 的变化过程为，-2•如果在，一北的过程中,对应的两数值
了元)无限接近于确定的数值 4,那么就说4 是的数广(心)当大天时的极限．当然,这里
我们首先假定两数广(x)在点，的某个去心邻城0内是有定义的
在，1的过程中,对应的两数值厂(工)无限接近于A,就是U/(北)-41能任意
小小•如数列极限概念所述，(x)-41能任意小这件事可以用1(*)-41<8米表达，
其中：是任意给定的正数 因为两数值广八)无限接近于A 是在，一的过程中实
现的，所以对于任意给定的正数：.只要求充分接近于，的，所对应的两数值

大(，)满足不等式11(×)-A1<e;而充分接近于玉的，可表达为0<lt-5ol<8,其中8
是某个正数，从儿何上看,适合不等式0<1*一51<8的，的全体，就是点去的去心8
邻域①,而邻城半径。则体现了，接近士的程度

通过以上分析，我们给出*-元时的数的极限的定义如下：
定义1设函数广不在点环的某一去心邻域内有定义． 如果存在常数A,对
手任意给定的正数e(不论它多么小),总存在正数8，使得当，满足不等式
0<1x-*,1<8 时,对应的西数值爪士)都满足不等式
If(a)-A1<E,

那么常数^就叫做西数（*)当，天,时的极限，记作
lim/（x)=4 或厂 一A（当x-下)
我们指出，定义中0<1x-501表示*天5所以工一去时广地)有没有极限，与
f(*在点和是否有定义并无关系
定义1可以简单地表述为
Linf( =ASve>0,38>0，当0<1x-501<8时,有1/(=1-41<6
两数广(i)当，點时的极限为4的几何解释如下-任意给定一正数E，作平
行于，轴的两条直线 了=A+e 和y=4-4，界于这两条直线之问是一横条区城． 根
据定义,对于给定的e,存在着点3的一个。邻城(56-6,56+8)
当y=/（天）的图形
上的点的横坐标＜在邻城（50一5,50+8)内但
*天时,这些点的纵坐标厂(x)满足不等式
1f（×)-41≤5.
或
A-6<f(x)<4+E
亦即这些点落在上面所作的横条区域内
（图 1-23)
例1证明limc=e,此处c为-
一常数.
10 ol
E8 1-23
证这里 -A1=16-cl=0,因此
Va>0.可任取 6-0,当 O<1-x01<8 时,能使不等式
I/(x) -Al = Ic-el = 0<8
成立.所以iime=e
S1

例2证明lima =x0。
•证这里1*)-41=1x-11,因此Ve>0,总可取8=6,当0<18-401<6=6时
能使不等式1(*-41=lx-501<e成立•所以lima=xo
例3证明lim(2x-1)=1.
证 由于
为了使IK(x)-Al<e,只要
1×=41=12×-1)派11=21×-11
18-11€
所以，Vo0,可取8-号,则当大适合不第式
0<x=11<8
时,对应的两数值广(¢）就满足不等式
1£×=11=1(2×-1)-11<8
从而
lim(2x-1) = 1.

证明lim
- = 2.
x-1
证这里,西数在点x=1是没有定义的,但是西数当×一1时的极限存在或
不存在与它并无关系•事实上，VE>0.将不等式
13-2z0
约去非零因子，-1后就化为
1x+1-21= 1×-11<8
因此，只要取8=6,那么当0<1x-11<8 时，就有
--2 <€.

所以

=2
例5证明：当对>0时,limva
证
Ve>0.因为
If(x) -Al = I Vx
-r|:
x-to要使1（5)-41<e,只要1x-x01<3。8且x三0,而x三0可用1-t01≤大保证,因此
•取8=min i xowtoei（这式子表示,6是，。和、/a。：两个数中较小的那个数），则
当x适合不等式 0<1x-x01<8 时,对应的两数值 、t就满足不等式
IVx -vtolse.
所以
上述x一时西数广(，）的极限概念中，x 是既从工的左侧也从工的右侧趋于
5的但有时只能或只需考虑，仪从工的左侧趋手5（记作*
一，的情形，或¢
仅以工的右侧道于北(记作x一*)的情形在，-的情形,士在…的左侧,t<
x在linf()=4的定义中,把0<14-501<8改为50-8<x<z。那么』就叫做两数
广x)当一地时的左极限，记作
limr(s)=A 或大x)=4
类似地，在limf(x)=4 的定义中,把0<15-501<8改为55x<56+5,那么4 就叫
做雨数广(x)当xx时的右极限,记作
limf(心)=4或大5=A
左极限与右极限统称为单侧极限
根据，x时两数广(s)的极限的定义以及左极限和右极限的定义,容易证
明：西数了(工)当，-x时极限存在的充分必要条件是左极限及右极限各自存在
并且相等，即
£1)=1 ).
因此，即使八好)和八心)都存在，但若不相等，则limr(）也不存在存在（图 1-24)
12自变量趋于无穷大时西数的极限
如果在，一∞的过程中，对应的西数值广(*)无限接
近于确定的数值 4,那么4叫做两数广：首大-西时的
极限． 精确地说,就是

定义2设西数f(x）当1x1大于某一正数时有定
义•如果存在常数A,对于任意给定的正数，(不论它多
么小)，总存在着正数不使得当，满足不等式
图 1-24

Ixl二X时,对应的西数值广(，)都满足不等式
mFxD-Alse.
;那么常数4 就叫做西数，（a)当*一口时的极限，记作
limf(x) = A
或大x-A（当业∞）

定义2可简单地表达为
limr(o=A V8>0.3x>0.省1x12x时，有1(x-A1<E.
如果 北>0且无限增大（记作t+∞)那么只要把上面忘义中的1x1>x改为
s>X,就可得lim f(x=4的定义同样，如果，<0日11无限增大（记作
2-∞）•那么只要把1x1>X改为大-不便得hin f(t-A的定义
从几何上来说，Himf(a）=4的意叉是：作直线y=A-6和y=A+8,则总有一个
正数x 存化，使得当路一x或子二天时，阿数，二大女)的图在位于这两直线之同(图
1-25）．这时•直线，=A 是两数了=f(:)的图形的水平渐近线.
例7证明lm
-=0.
证
不等式
-0∞
成立• 因这个不等式相当于
1aTSe或12151
图 1-25
1

我的理解

V7．函数极限的性质

与收敛数列的性质相比较，可得两数极限的一些相应的性质．它们都可以根
据两数极限的定义,运用类似于证明收敛数列性质的方法加以证明．由于丽数极
限的定义按自变量的变化过程不同有各种形式，下面仅以“lim/(a)“这种形式为
Lenaisi
代表给出关于两数极限性质的一些定理，并就其中的儿个给出证明． 至于其他形
式的极限的性质及其证明，只要相应地做一些修改即可得出

定理1（函数极限的唯一性）如果limf(s）存在,那么这极限唯一
40

定理2（函数极限的局部有界性）如果lim/(s)=4,那么存在常数M>0和8
>0,使得当 0<1x-x01<8 时，有1f(=21≤.M

证
因为limf(x)三A,所以取§=1,则日6>0,当0<12-x01<8时，有
1£-41≤1=1£1≤1$-41+141≤141+1.
记 M=1A1+1,则定理2就获得证明

定理 3（西数极限的局部保号性）
如果limf(=)=A,且A>0（或A<0）,那么
存在常数6-0,使得当 0<1z

-51<8 时，有广(+)>0（或f(*)<0)
证就A>0的情形证明
因为IinF(s)=A>0,所以,取。=2
->0,则35>0，当0<lx-t01<8 时，有
A
A
= f(x) >A -2
=2
A>0.
类似地可以证明 A<0 的情形
siy
从定理3的证明中可知,在定理了的条件下,可得下面更强的结论：
定理 3”
如果limf(D=A （A*0),那么就存在着北的某一去心邻域U(5）,
当xE0（）时，就有1/rC+）1I41
由定理3,易得以下推论：
推论 如果在，的某去心邻域内八 =0（或八 ≤0）,而且limr=4.那左极限与右极限统称为单侧极限．
根据x-1时两数广(x）的极限的定义以及左极限和右极限的定义
明：西数f工)当，50时极限存在的充分必要条件是左极限及右极限秀
并且相等，即
因此,即使广(下。）和f( ）都存在，但若不相等,则江nf(工)也不存在
例6
设
f(x) =
10.!
1<0.
+ =0
*>0
证明：当二0时大的极限不存在
证
仿例3可证当1-0时长的左极限
limf(a)= lim(x-1)=
_1,
-0
-0
而右极限
lim/(x) = lim (x+1) = 1
因为左极限和右极限存在但不相等，所以不存在（图 1-24)
12自变量趋于无穷大时西数的极限
如果在，一∞的过程中，对应的西数值广(*)无限接
近于确定的数值 4,那么4叫做两数广：首大-西时的
极限． 精确地说,就是

定义2设函数f(x）当1x1大于某一正数时有定
义•如果存在常数A,对于任意给定的正数，(不论它多
么小)，总存在着正数不使得当，满足不等式
图 1-24

Ixl二X时,对应的西数值广(，)都满足不等式
mFxD-Alse.
;那么常数4 就叫做西数，（a)当*一口时的极限，记作
limf(x) = A
或大x-A（当业∞）
定义2可简单地表达为
limr(o=A V8>0.3x>0.省1x12x时，有1(x-A1<E.
如果 北>0且无限增大（记作t+∞)那么只要把上面忘义中的1x1>x改为
s>X,就可得lim f(x=4的定义同样，如果，<0日11无限增大（记作
2-∞）•那么只要把1x1>X改为大-不便得hin f(t-A的定义
从几何上来说，Himf(a）=4的意叉是：作直线y=A-6和y=A+8,则总有一个
正数x 存化，使得当路一x或子二天时，阿数，二大女)的图在位于这两直线之同(图
1-25）．这时•直线，=A 是两数了=f(:)的图形的水平渐近线.
例7证明lm
-=0.
证
不等式
-0∞
成立• 因这个不等式相当于
1aTSe或12151
图 1-25
1
V7-、西数极限的性质
与收领数列的性质相比较,可得两数极限的一些相应的性质， 它们都可以根
据兩数极限的定义,运用类似手证明收敛数列性质的方法加以证明．由于两数极
限的定义按自变量的变化过程不同有各种形式，下面仅以“lim(*)*这种形式为
代表给出关于两数极限性质的一些定理,并就其中的几个给出证明… 至手其他花
式的极限的性质及其证明，只要相应地做一些修改即可得出

定理1（函数极限的唯一性）如果lim(z)存在,那么这极限唯

定理2（函数极限的局部有界性）如果limr(a)=4,那么存在常数1>0和8

＞0,使得当 0<1x-x01<8时，有If(=21≤4
证因为limf(5)=4,所以取5=1列96-0当0<11-50158时，有
1£=41≤1=1×1≤1×-41+141≤141+1
记 M=1A1+1,则定理2就狹得证明
定理 3（西数极限的局部保号性）如果lim/(*)=4,旦4>0（或A<0）,那么
存在常数6>0,使得当 0<1*-101<8时，有大( 二0（或九地<0
证就A>0的情形证明
因为lir(x=4>0.所以取a=
A
2
>0. 38>0, 40<- I <8
A
If(x)-Al<2
- f(x)>A-.
A =2
类似地可以证明 A<0的情形.
sing
从定理3的证明中可知，在定理3的条件下，可得下面更强的结论：

定理3，
如果limr(N)=A （A*0）,那么就存在著，的某一去心邻域U(玉）
当*E0（元)时,就有1r( 13141
由定理3.易得以下推论：

推论
如果在，的某去心邻域内八 ≥0（或八 ≤0）,而且linr()=4,那A≥0（或4≤0）.

•定理 4（西数极限与数列极限的关系）
妇果极限limf(x)存在，1.！为函
+20
数广(心）的定义域内任一收敛于×的数列，且满足：2.*50（nEN.）,那么相应的
函数值数列if(2)」必收敛，且limf(x.)=limf(2).

^-
证设limf()=A,则Ve>0,38>0,当0<15-501<8时，有1/(1)-A1<E.
-+.0
叉因limx.三x,故对8>0,彐N,当几>N时，有15.-501<8.
由假设，X
•大心（nEN.），故当几＞N时,0<1x.一501<0，从而
Ifx.)-A1<e．即limf(xn)=4.

总结：