试题 A: 空间

题目

【问题描述】
小蓝准备用 256MB 的内存空间开一个数组，数组的每个元素都是 32 位
二进制整数，如果不考虑程序占用的空间和维护内存需要的辅助空间，请问
256MB 的空间可以存储多少个 32 位二进制整数？

解析

答案：67108864
1MB=1024KB
1KB=1024B
1B=8bit
1位即是1bit
ans=256*1024*1024*8/32=67108864

试题 B: 卡片

题目

【问题描述】
小蓝有很多数字卡片，每张卡片上都是数字 0 到 9。
小蓝准备用这些卡片来拼一些数，他想从 1 开始拼出正整数，每拼一个，
就保存起来，卡片就不能用来拼其它数了。
小蓝想知道自己能从 1 拼到多少。
例如，当小蓝有 30 张卡片，其中 0 到 9 各 3 张，则小蓝可以拼出 1 到 10，
但是拼 11 时卡片 1 已经只有一张了，不够拼出 11。
现在小蓝手里有 0 到 9 的卡片各 2021 张，共 20210 张，请问小蓝可以从 1
拼到多少？
提示：建议使用计算机编程解决问题。

解析

答案：3181
直接编程：

#include<bits/stdc++.h>
using namespace std;using namespace std;
int cnt[10]; 
int main() {int n=2021,i,x,k=1;for(i=0;i<10;i++)cnt[i]=n;while(1){x=k;while(x){if(cnt[x%10]>0)cnt[x%10]--,x/=10;else break;}if(x)break;else k++;}cout<<k-1<<endl;return 0;
}

运行结果：
在这里插入图片描述

试题 C: 直线

题目

【问题描述】
在平面直角坐标系中，两点可以确定一条直线。如果有多点在一条直线上，
那么这些点中任意两点确定的直线是同一条。
给定平面上 2 × 3 个整点 {(x, y)|0 ≤ x < 2, 0 ≤ y < 3, x ∈ Z, y ∈ Z}，即横坐标
是 0 到 1 (包含 0 和 1) 之间的整数、纵坐标是 0 到 2 (包含 0 和 2) 之间的整数
的点。这些点一共确定了 11 条不同的直线。
给定平面上 20 × 21 个整点 {(x, y)|0 ≤ x < 20, 0 ≤ y < 21, x ∈ Z, y ∈ Z}，即横
坐标是 0 到 19 (包含 0 和 19) 之间的整数、纵坐标是 0 到 20 (包含 0 和 20) 之
间的整数的点。请问这些点一共确定了多少条不同的直线

解析

答案：40257
直接编程，用y=kx+b把所有的直线存起来，最后加上20条斜率不存在和21条斜率为0的直线。有个细节是，如果直接用kb的话，精度会炸。
我比赛时的关键代码

#include<bits/stdc++.h>
using namespace std;using namespace std;
pair<double ,double>t;
map<pair<double ,double>,int>q;
int main() {int x1,x2,y2,y1,n=20,m=21;for(x1=0;x1<n;x1++){for(x2=0;x2<n;x2++){for(y1=0;y1<m;y1++){for(y2=0;y2<m;y2++){if(x1!=x2){t.first=1.0*(y1-y2)/(x1-x2);t.second=y1-t.first*x1;q[t]++;}}}}}cout<<q.size()+n;return 0;
}

运行结果：
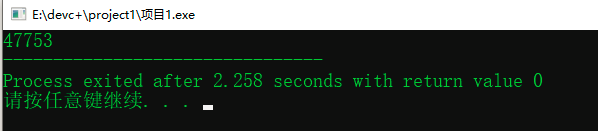
在这里插入图片描述
然后精度炸了，数字偏大。

比赛结束后，写了一份换成分数形式：

#include<bits/stdc++.h>
using namespace std;
pair<int ,int>t1,t2;
pair<pair<int ,int>,pair<int ,int> >tt;
map<pair<pair<int ,int>,pair<int ,int> >,int>q;
int gcd(int a,int b){if(a<b)return gcd(b,a);if(b==0)return a;return gcd(b,a%b);
} 
void ggcd(int &a,int &b){int t=gcd(abs(a),abs(b));if(a>0&&b>0)a/=t,b/=t;else if(a<0&b<0)a/=-t,b/=-t;else if(a!=0&&b!=0){a/=t;b/=t;if(a<0)a=-a,b=-b;}else {a=0;b/=t;}
}
int main() {int x1,x2,y2,y1,n=20,m=21;for(x1=0;x1<n;x1++){for(x2=0;x2<n;x2++){for(y1=0;y1<m;y1++){for(y2=0;y2<m;y2++){if(x1!=x2&&y1!=y2){t1.first=y1-y2;t1.second=x1-x2;ggcd(t1.first,t1.second);//y=kx+b-->b=y-kx-->b=(y*t1.second-t1.first*x)/t1.second;t2.first=y1*t1.second-t1.first*x1;t2.second=t1.second;ggcd(t2.first,t2.second);tt.first=t1;tt.second=t2;q[tt]++;//printf("y=(%d/%d)x+(%d/%d)\n",t1.first,t1.second,t2.first,t2.second);}}}}}cout<<q.size()+n+m;return 0;
}

运行结果：
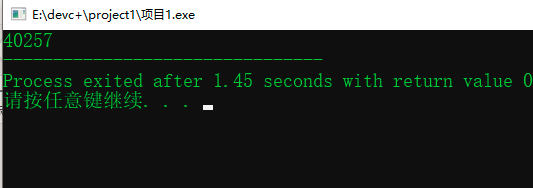
在这里插入图片描述

总结反思一下：直接暴力用double居然炸了精度，，，，，蓝桥再也不是我认识的那个暴力蓝桥杯了。。。

试题 D: 货物摆放

题目

小蓝有一个超大的仓库，可以摆放很多货物。
现在，小蓝有 n 箱货物要摆放在仓库，每箱货物都是规则的正方体。小蓝
规定了长、宽、高三个互相垂直的方向，每箱货物的边都必须严格平行于长、
宽、高。
小蓝希望所有的货物最终摆成一个大的立方体。即在长、宽、高的方向上
分别堆 L、W、H 的货物，满足 n = L × W × H。
给定 n，请问有多少种堆放货物的方案满足要求。
例如，当 n = 4 时，有以下 6 种方案：1×1×4、1×2×2、1×4×1、2×1×2、 2 × 2 × 1、4 × 1 × 1。
请问，当 n = 2021041820210418 （注意有 16 位数字）时，总共有多少种
方案？
提示：建议使用计算机编程解决问题。

解析

涉及数学组合问题。
假设体积是V, 那么找出所有的质因子放进LWH三个位置，答案就是看有几种放法。
质因子不同时：
比如6=2*3
那就是（2的放法）*（3的放法）。即3*3=9。
质因子相同时：
我们可以看成下面这样的问题：
假设现在有n个一样的球，放进3个盒子（盒子可以不放球），求几种放法。
解决：用挡板法，用两个挡板把球隔开，这样三个部分放进三个盒子。第一块挡板有（n+1）种放法，第二块挡板有（n+2）种放法，/2除去重复，所以就是（n+1）*（n+2）/2。
说明：4(两个质因子2)
加粗的是第一块挡板
第一块挡板：（两个因子下第一块挡板三个放法，最左到最右）
① | 2 2，或者②2 | 2，或者③2 2 | ；
第二块挡板：（两个因子下+一块挡板，第二块挡板四个放法，最左到最右）
①的情况下：| | 2 2， | |2 2， | 2|2， | 2 2|
②的情况下：|2 | 2，2| | 2，2 || 2，2 | 2 |
③的情况下：|2 2 | ，2|2 | ，2 2| | ，2 2 | |
所以3*4=12
第一块挡板放在a位置、第二块挡板放在b位置与第一块挡板放在b位置、第二块挡板放在a位置相同,去重/2
4分成2^2,有3*4/2=6种放法。

找出2021041820210418所有因子。
在这里插入图片描述
所以ans=3*3*3*3*3*((3+1)*(3+2)/2)=243*10=2430

源码：

#include<bits/stdc++.h>
using namespace std;using namespace std;
#define ll long long
map<ll,int>q;
int main() {ll n= 2021041820210418,i;for(i=2;i*i<=n;i++){while(n%i==0){q[i]++;n/=i;}}if(n!=1)q[n]++;for(map<ll,int>::iterator it=q.begin();it!=q.end();it++){cout<<it->first<<" :"<<it->second<<endl;}return 0;
}

试题 E: 路径

题目

【问题描述】
小蓝学习了最短路径之后特别高兴，他定义了一个特别的图，希望找到图
中的最短路径。
小蓝的图由 2021 个结点组成，依次编号 1 至 2021。
对于两个不同的结点 a, b，如果 a 和 b 的差的绝对值大于 21，则两个结点
之间没有边相连；如果 a 和 b 的差的绝对值小于等于 21，则两个点之间有一条
长度为 a 和 b 的最小公倍数的无向边相连。
例如：结点 1 和结点 23 之间没有边相连；结点 3 和结点 24 之间有一条无
向边，长度为 24；结点 15 和结点 25 之间有一条无向边，长度为 75。
请计算，结点 1 和结点 2021 之间的最短路径长度是多少。
提示：建议使用计算机编程解决问题。

解析

答案：10266837
dij不会写
Floyd已经忘了
那就猜吧
从1到2021，那么我只要走得尽量少，且边尽量短就好。
lcm（a,b）=a*b*gcd(a,b)
如果a!=b&&a>1&&b>1，那么gcd(a,b)肯定<=abs(a-b)，所以gcd最大就是21,我让gcd(a,b)始终保持21
取点1,21,42,63,84，… ，2016,2021
运行结果：
在这里插入图片描述
ans=10266837