论文全名:Beyond Correlation Filters: Learning Continuous Convolution Operators for Visual Tracking
论文摘自ECCV 2016,由Martin Danelljan(目标跟踪大神)、Gustav Häger、Fahad Shahbaz Khan、Michael Felsberg撰写
附上C-COT的变体ECO的预训练网络地址:预训练网络参数
摘要
DCF(判别相关滤波器)特点:通过包括训练样本的所有移位来提取负样本(只限于单分辨率特征图)。
作者基于DCF,提出训练连续卷积滤波器:在连续空间域中,用隐式插值模型训练。
特点:(1)在多分辨率深度特征图中处理高效;(2)算法可以进行亚像素定位,对精确特征点跟踪任务表现突出;(3)同时在广泛特征点跟踪实验中表现不错。
1 前言
(1)DCF:利用离散傅立叶变换解决训练样本的所有空间移位(在VOT2014、OTB2015都有广泛应用),缺点:只限于单分辨率特征图。
(2)基于DCF的DCNN(DeepSRDCF与HCF等):利用浅卷积层来进行图像分类(空间分辨率更高),缺点:在DCF基础上融合多个层仍未解决。
作者提出:

(2)作者提出的连续卷积滤波器f
(3)对这三层的连续卷积层输出:置信度分数
(4)输出目标的连续置信度函数
在连续空间域中训练一个卷积算子(用训练样本学习一个隐式插值模型),将学习的一组卷积滤波器产生目标的连续域置信度图,将该卷积滤波器与多分辨率特征图(或者亚像素、特征点跟踪)融合。
2 相关工作
DCF(用循环相关以滑窗形式训练回归器):
(1)单通道特征:MOSSE、核化tracking-by-detection
(2)多通道特征(可以结合HOG和颜色等高维特征):CN、MCCF、DSST、SAMF(尺度估计)、KCF、LCT(非线性核)、SRDCF、ZACFs、CFLM(减弱循环卷积的周期性)。
DCNN:
(1)最后一个卷积层用于图像分类(特点:判别力,有高级视觉信息)
(2)第一个卷积层用于视觉跟踪:DeepSRDCF。(特点:高空间分辨率下具有低特征,利于定位)。
特征点跟踪
(1)经典的Kanade-Lucas-Tomasi(KLT)跟踪算法:(生成模型)最小化两个图像块之间的差异的平方和
(2)改进版的KLT跟踪器。
(3)作者提出一种判别学习方法。
作者提出:在连续空域中学习一个判别卷积算子。
特点:(1)可以集合多分辨率特征映射:卷积层与多分辨率HOG、颜色特征的组合。
(2)可以实现精确的亚像素定位。
3 训练连续卷积算子
【1】准备工作
空间:希尔伯特空间![]() ,标准正交基为:
,标准正交基为:![]() ,其中
,其中![]() 。
。
在周期函数![]()
![]() 中,考虑复函数g,满足T> 0且平方勒贝格可积。
中,考虑复函数g,满足T> 0且平方勒贝格可积。
定义:设![]() ,内积满足
,内积满足![]() ;循环卷积运算:
;循环卷积运算:![]() ,其中
,其中![]() 。
。
性质:
(1)设g的离散傅立叶系数为![]() ,那么
,那么![]() 。
。
(2)![]()
![]() (Parseval等式)
(Parseval等式)![]()
![]() (
(![]() 范数的性质)。
范数的性质)。
(3)离散傅立叶系数满足两个卷积特性:![]() 与
与![]() ,其中
,其中![]() 。
。
【2】连续训练(整体过程)
输入:第j帧(以目标框为中心长宽各放大5倍)图像块![]() 的特征图(用imagenet-vgg-m-2048预训练的结果):
的特征图(用imagenet-vgg-m-2048预训练的结果):![]() (共D个特征通道)
(共D个特征通道)

目的:训练一个连续卷积算子![]() 。
。
记![]() 为第d个特征通道的训练样本数,
为第d个特征通道的训练样本数,![]() 为其索引值,则样本空间为
为其索引值,则样本空间为![]() 。
。
(1)引入隐式插值模型:
定义特征通道的区间为![]() (
(),第d个特征通道的插值算子为
![]() (从欧式空间到希尔伯特空间的映射),
(从欧式空间到希尔伯特空间的映射),
![]() 其中,
其中,![]() ,
,![]() 可看作希尔伯特空间的标准正交基,那么式(2)则表示为插值基函数偏移的叠加。
可看作希尔伯特空间的标准正交基,那么式(2)则表示为插值基函数偏移的叠加。
特点:与DCF类似(周期性),上式对特征图做了周期性扩展。

(2)【欧式空间:针对连续区间![]() 】定义置信度函数:
】定义置信度函数:![]()
![]() 。(一维)
。(一维)
特点:与其他判别法类似,最大化图像区域中的置信度得分来定位目标。而关键区别在于置信度函数是在连续空间域上定义的,因此可用于更高精度地定位目标。
(3)【希尔伯特空间:针对所有的空间域】计算样本x的卷积算子(置信度函数)
定义一组(有特征通道![]() 区分的)连续卷积滤波器
区分的)连续卷积滤波器![]() 。
。
卷积算子(连续)为所有通道的卷积和:![]() ,其中,(根据循环卷积性质)
,其中,(根据循环卷积性质)![]()
![]() 。
。

(4)【希尔伯特空间:针对所有的空间域】定义样本![]() 的期望输出:
的期望输出:![]()
![]() 。
。
特点:对亚像素处理更加精确。

(5)计算滤波器f:
定义训练样本对![]() ,最小化损失函数
,最小化损失函数![]() 即可得到滤波器f。其中,空间正则化项与SRDCF类似。
即可得到滤波器f。其中,空间正则化项与SRDCF类似。

特点(对于![]() ):
):
正则项可以控制滤波器f的空间范围(图像区域任意);
对于背景特征的空间区域,![]() 值较大;
值较大;
![]() 在[0,T]上定义,并周期性地扩展到
在[0,T]上定义,并周期性地扩展到![]() ,即由多个傅立叶系数
,即由多个傅立叶系数![]() 组成:
组成:
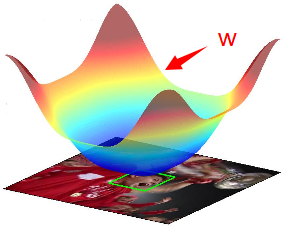
接下来,我们使用提出的公式(4)推导出训练连续滤波器f的过程。
【2-1】训练滤波器f(傅立叶变换)
目的:在傅立叶域中最小化式(4)。
(1)设![]() 的离散傅立叶变换为
的离散傅立叶变换为![]() ,其中,
,其中,![]() ,插值特征图的傅立叶系数为:
,插值特征图的傅立叶系数为:![]() 。
。
(2)由【1】准备工作中傅立叶变换的卷积性质,可得到置信度函数的傅立叶系数:
![]()
![]() 。
。
(3)由【1】准备工作中Parseval公式放入式(4)中,得到损失函数:
![]()
![]()
![]()
![]()
![]()
![]()
出于实际目的,滤波器f需要由一组有限的参数表示。
(4)考虑子空间(有限维)![]()
![]() (对于第d个特征通道,当
(对于第d个特征通道,当![]() 时,有
时,有![]() ,即
,即![]() (设定
(设定![]() )决定了滤波器
)决定了滤波器![]() 的系数数量),
的系数数量),
【a】定义非零向量![]() ,其中,
,其中,![]()
![]() ,
,
【b】设![]() ,对于期望输出
,对于期望输出![]() ,其中,
,其中,![]() ,
,
【c】对于式(6)的正则项,设![]() 为
为![]() 的非零系数数量(当
的非零系数数量(当![]() 时,有
时,有![]() ),定义满足
),定义满足![]() 的矩阵
的矩阵![]() (Toeplitz矩阵),其大小为
(Toeplitz矩阵),其大小为![]() :
:
 。
。
【d】定义非零块矩阵![]() ,其中由矩阵
,其中由矩阵![]() 组成,其中,
组成,其中,,
【e】根据式(6),(与SRDCF中相同)可得到有限维空间V中的损失函数为:![]() ,其中,
,其中,![]() 表示标准欧几里德范数。
表示标准欧几里德范数。
【f】对式(7)的![]() 求一阶导(目的:损失函数最小化):
求一阶导(目的:损失函数最小化):
(8)
其中,![]() ,H表示矩阵共轭转置。
,H表示矩阵共轭转置。
(5)注意,如果w具有少量的非零傅里叶系数w[k],则(8)形成稀疏线性方程。
在进行跟踪时,采用共轭梯度法迭代求解式(8);对特征点跟踪时,使用单通道特征映射和常数w。
【2-2】期望输出y与插值函数b
(1)定义一个周期函数![]() ,其中
,其中![]() ,利用【1】准备工作中内积的定义,由泊松求和公式可得到:
,利用【1】准备工作中内积的定义,由泊松求和公式可得到:![]() 。
。
(2)记![]() 为样本
为样本![]() 中目标的估计位置,期望输出
中目标的估计位置,期望输出![]() 为一维高斯函数(
为一维高斯函数(![]() )的周期函数,则其傅立叶系数为:
)的周期函数,则其傅立叶系数为:![]() 。
。
(3)记![]() 为三次样条插值核函数,插值函数
为三次样条插值核函数,插值函数![]() =
=![]() (
(![]() 的缩放平移),则其傅立叶系数为:
的缩放平移),则其傅立叶系数为:![]() 。
。
【3】高维度扩展
考虑二维情况。
空间:希尔伯特空间![]() ,标准正交基为:
,标准正交基为:![]()
![]() 。对应滤波器f的训练也可从【3】中对应得到。
。对应滤波器f的训练也可从【3】中对应得到。
期望输出![]() 为二维高斯函数,插值函数b为三次样条插值核的可分离组合:
为二维高斯函数,插值函数b为三次样条插值核的可分离组合:![]() 。
。
4 跟踪框架
基于最大化连续置信度函数。
【1】定位
目的:利用滤波器f定位目标。
(1)图像中感兴趣区域中提取特征图![]() 。
。
(2)用式(5)计算置信度函数![]() 的傅里叶系数。
的傅里叶系数。
(3)采用两步法最大化区间![]() 上的得分
上的得分![]() :
:
1.粗略估计【离散】(执行网格搜索):对于![]() ,用
,用![]() 估计置信度函数。即
估计置信度函数。即![]() 的缩放逆离散傅立叶变换。
的缩放逆离散傅立叶变换。

2.将其最大值(记作![]() )作为初始值,通过
)作为初始值,通过![]() 的解析微分来计算梯度和Hessian。
的解析微分来计算梯度和Hessian。

【2】目标测试
设定:
(1)学习率参数λ= 0.0075,权重为![]() ,然后将权重归一化,使得
,然后将权重归一化,使得![]() 。
。
(2)m = 400(最多包含)
(3)检测目标方法:执行多尺度搜索(与SRDCF与SAMF相同),有5个尺度和相对1.02的比例因子,然后用【1】中网格搜索方法(五次牛顿迭代)最大化置信度。
(4)迭代式(8)来完成:初始帧迭代100次,后续帧迭代5次。

【3】特征点测试
输入:一张灰度图
设在单通道特征图(D = 1)中,设![]() 为常函数,那么式(8)可化简为:
为常函数,那么式(8)可化简为:
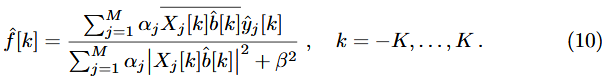
5 实验
目标跟踪:OTB-2015,Temple-Color和VOT2015。
特征点跟踪:MPI Sintel。
【1】评估在跟踪中融合来自深层网络的多个卷积层的影响:


Layer 0:输入RGB图像层;Layer 1:第一个卷积层;Layer 5:最后一个卷积层。
【2、目标跟踪】OTB-2015、Temple-Color与VOT2015数据集
算较:C-COT、ASLA、TLD、Struck、LSHT、EDFT、DFT、CFLB、ACT、TGPR、KCF、DSST、SAMF、MEEM、DAT、LCT、HCF、Staple和SRDCF、SRDCFdecon、DeepSRDCF。




【3、特征点跟踪】MPI Sintel数据集
数据集特点:由23个序列组成
评估方法:在每个序列的第一帧中选择大约2000个特征点进行评估。
算法比较:MOSSE、C-COT(学习率都为![]() ,正则参数都为
,正则参数都为![]() )和KLT(逐帧跟踪特征点)、Ours-FF(学习率
)和KLT(逐帧跟踪特征点)、Ours-FF(学习率![]() )。
)。